Summen lassen sich in DeltaMaster auf vielfältige Weise einblenden, wie schon Gerald Butterwegge in den DeltaMaster clicks! 12/2009 beschrieben hat. Die meisten dieser Summen werden von der zugrundeliegenden OLAP-Datenbank in Form von Aggregationen entlang von hierarchischen Strukturen bereitgestellt. Sind mehrere Strukturen in einer Pivottabelle verschachtelt, ergeben sich durch die Kombination der Summen- und Dimensionselemente oft mehr Zwischensummenzeilen als gewünscht. Der folgende Blogbeitrag zeigt, wie mittels MDX-Mengendefinitionen die Kombination von verschachtelten Elementen exakt auf die jeweiligen Berichtsanforderungen angepasst wird.
Um jedoch gleich hier der Forderung nach flexiblen Zwischensummen in DeltaMaster zu begegnen, zunächst eine Abgrenzung von OLAP-Aggregationen und Tabellenaggregationen in DeltaMaster.
Aggregationen vs. Summenzeilen
Grundsätzlich sind die OLAP-Aggregationen den Tabellenaggregationen in DeltaMaster vorzuziehen, da die OLAP-Aggregationen auch für nicht additive Kennzahlen wie prozentuale Abweichungen, Anteile oder Mittelwerte – bei entsprechender Definition der Berechnungsreihenfolge (SOLVE ORDER) – korrekt berechnet werden.
Folgendes Beispiel verdeutlicht dies:
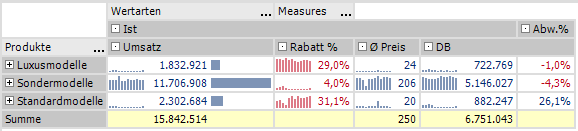
Abb. 1: Summenzeilen in einer Pivottabelle: Für nicht additive Kennzahlen wird die Summe nicht berechnet.
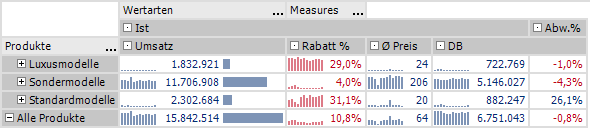
Abb. 2: OLAP-Aggregationen werden auch für nicht additive Kennzahlen korrekt berechnet.
Aggregationen vs. Mittelwert
Der erfahrene DeltaMaster-Anwender wird jetzt auf die Mittelwert-Aggregation in der Pivottabelle verweisen. Doch hierbei ist zu beachten, dass die Mittelwertberechnung in der Pivottabelle den Mittelwert der dargestellten Werte berechnet. Die OLAP-Aggregation wird jedoch auf der Aggregationsebene selber gerechnet, bei Durchschnittswerten oder Anteilen wird also einen gewichteter Mittelwert berechnet.
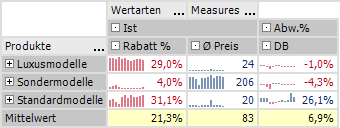
Abb. 3: Mittelwertzeile in der DeltaMaster-Pivottabelle
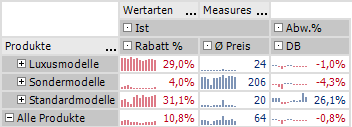
Abb. 4: OLAP-Aggregationen sind meistens als gewichtete Mittelwerte definiert
Verschachtelte Aggregationen
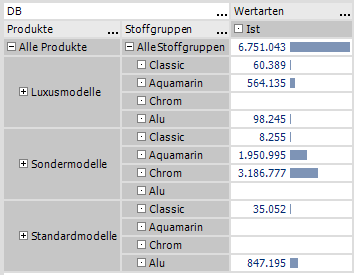
Schon bei der Verschachtelung von zwei Strukturen auf einer Pivottabellenachse ergeben sich mehr Summenkombinationen als normalerweise gewünscht sind. So sind beispielsweise die Zeilen 4-7 in der folgenden Abbildung in vielen Reportinganwendungen unerwünschte Zwischenzeilen.
Abb. 5: Verschachtelte Strukturen
Die Lösung liegt hier in einem einfachen MDX-Statement unter Verwendung des CROSSJOIN–Operators (*) und der Mengenverkettung (+):
{<view4>}* {<view5>}
+
<view4>.Children* <view5>.Children
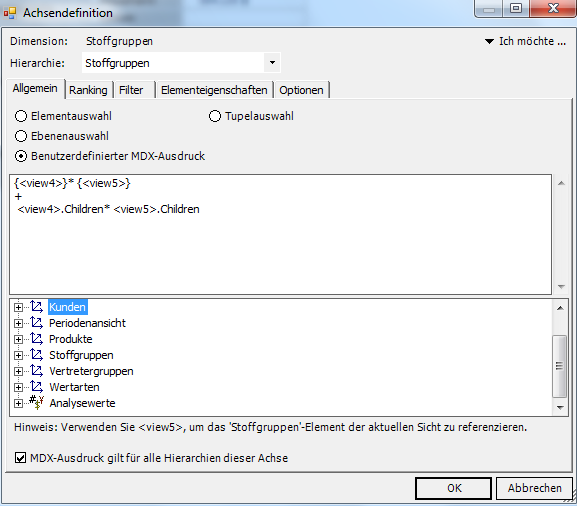
Das Statement ist in den Achsendefinitionsdialog einzutragen. Dabei darf die Option MDX Ausdruck gilt für alle Hierarchien dieser Achse nicht vergessen werden. Der Platzhalter ist kein Bestandteil von MDX, sondern eine Referenz auf die aktuelle Sicht.
Abb. 6: Achsendefinitionsdialog für hierarchieübergreifende MDX-Ausdrücke
Abb. 7: Verschachtelte Strukturen mit MDX
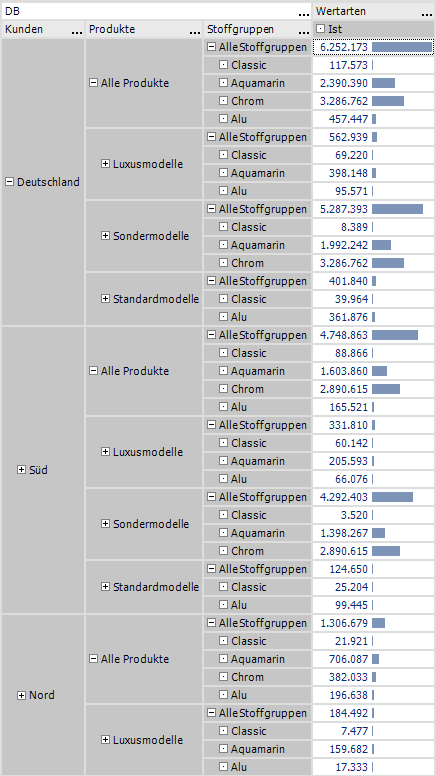
Bei drei verschachtelten Dimensionen vervielfacht sich die Zahl der unerwünschten Summenzeilen. Soll beispielsweise neben der Gesamtsumme (Deutschland, Alle Produkte, Alle Stoffgruppen) für jedes Gebiet nur die in Bild 7 gezeigte reduzierte Kombinatorik wiederholt werden, so enthält die vollständige Verschachtelung 35 unerwünschte Zeilen von insgesamt 100 möglichen Zeilen. Durch ausgeblendete Nullzeilen ergibt sich ein etwas anderes Verhältnis, das Grundproblem bleibt jedoch bestehen.
Abb. 8: Vollständige Verschachtelung von drei Dimensionen mit jeweils zwei Ebenen (Abbildung abgeschnitten)
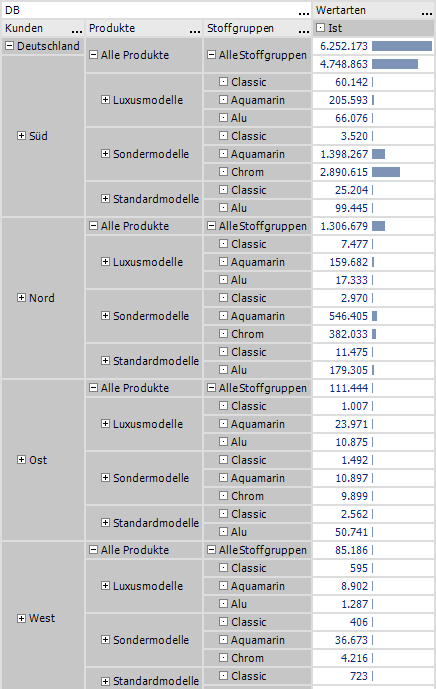
Auch hier liegt die Lösung in einem MDX-Statement: Ergänzend zum obigen Beispiel wird jetzt die reduzierte Verschachtelung der Produktstrukturelemente mit den Stoffgruppen für alle Gebiete wiederholt. Teilnehmer unserer MDX-Schulungen haben gelernt bei ‚für alle’ sofort an die Generate-Funktion zu denken, welche die gewünschte Iteration liefert:
{<view1>} * {<view4>} * {<view5>}
+
Generate(<view1>.Children,
{[Kunden].[Kunden].CurrentMember} * {<view4>} * {<view5>}
+
[Kunden].[Kunden].CurrentMember*<view4>.Children*<view5>.Children
)
Abb. 9: reduzierte Verschachtelung mit drei Dimensionen (Abbildung abgeschnitten)
Für ein tieferes Verständnis der MDX-Ausdrücke, insbesondere der Unterscheidung zwischen Dimensionselementen, Mengen von Dimensionselementen und mehrdimensionalen Tupeln bzw. Zelladressen, empfehlen wir die MDX-Schulungsunterlagen oder einen Besuch dieser Schulung.
In künftigen DeltaMaster-Versionen steht für die benutzerdefinierte Verschachtelung von Dimensionsebenen eventuell ein dem Tupeleditor ähnlicher Verschachtelungsassistent zur Verfügung.