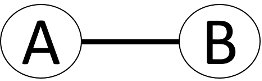Mit dem SQL Server 2017 wurden auch Graph-Datenbanken im SQL-Server eingeführt. Mit der neuesten Version SQL Server 2019 sind diese nun noch mit einigen Features unterstützt worden. Graph-Datenbanken stellen eine andere Art von Datenbank dar, in der Fragestellungen, wie z. B. Kürzeste-Wege-Probleme effektiver gelöst werden können als mit relationalen Datenbanken.

Allgemein gilt: Jedes Problem, dass man mit Graph-Datenbanken lösen kann, kann man auch mit relationalen Datenbanken lösen, allerdings schon bei einfachen Graphen kann dies zu erheblich mehr Arbeit beim Programmierer führen.

Die neuen Features der SQL-Graph-Datenbanken sollen im Folgenden anhand von einigen Beispielen aufgezeigt werden.

Graphen und Graphen-Datenbanken?

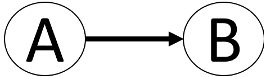
Graphen sind mathematische Modelle, in denen Abhängigkeiten zwischen Objekten in Beziehung gesetzt werden. Dies wird in folgendem zweidimensionalen Bild veranschaulicht:

Abbildung 1

In diesem Fall sind die Knoten {A, B} mit einer Kante (Pfeil) verbunden. Weil der Pfeil von A auf B zeigt, nennt man dies eine gerichtete Kante oder einen gerichteten Graphen. Wäre der Graph ungerichtet, dann würde das Bild folgendermaßen aussehen:

Abbildung 2

Hier könnte man sowohl von A auf B als auch von B auf A schließen.

Das bekannteste Problem, dass man aus dem Alltag kennt, welches mit Graph-DBs ausgedrückt werden kann, ist sicherlich ein Routing mit z.B. Google-Maps von einem Knoten zu einem anderen Knoten.

Abbildung 3

Beim SQL-Graph-DB-Modell werden nur gerichtete Graphen betrachtet. Möchte man eine ungerichtete Verbindung zwischen zwei Knoten ausdrücken, müsste man dies mit zwei gerichteten Verbindungen von A nach B und von B nach A beschreiben.

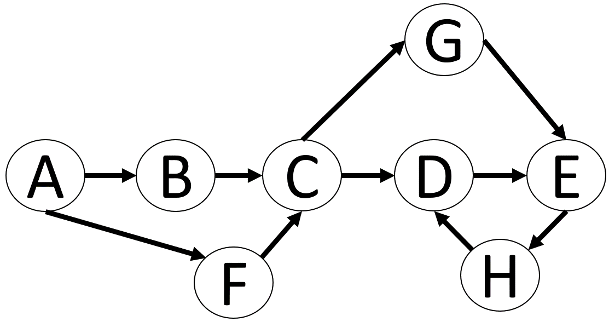
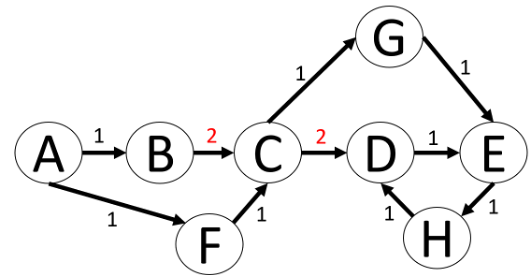
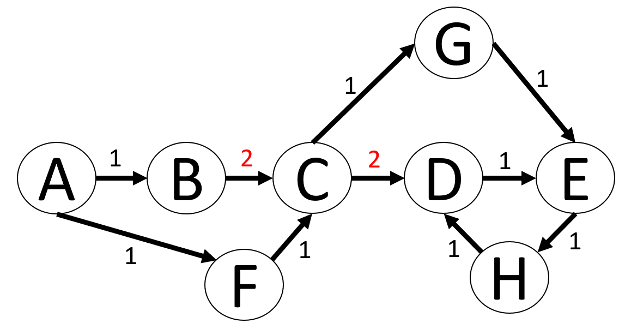
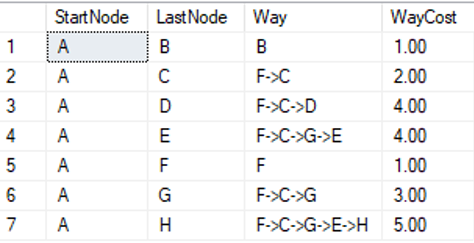
In dem Graph in Abbildung 3 ist zu erkennen, weshalb eine relationale Betrachtung schwierig werden kann. Eine Möglichkeit wäre, dies ähnlich einer Parent-Child-Beziehung zu sehen und diese Tabelle dann mit rekursiven CTEs durchsuchen zu lassen. Wenn man allerdings nach dem kürzesten Weg von Knoten A nach Knoten E sucht, dann muss man sich mit sehr komplizierten Abbruchbedingungen innerhalb der CTE beschäftigen, um z.B. Schleifen wie zwischen den Knoten D, E und G zu vermeiden.

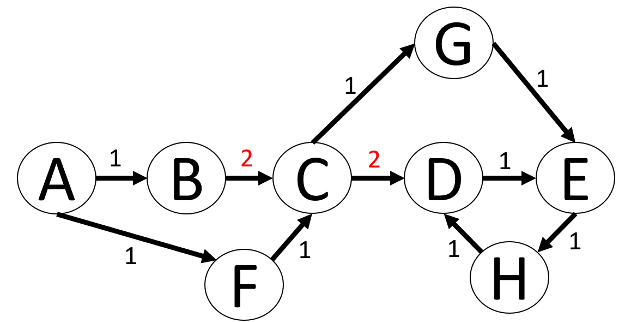
Zusätzlich wird der Graph noch mit Kantenwerten versehen, dadurch haben bestimmte Pfade durch den Graph Kosten bekommen. Zuvor waren alle Kanten gleichwertig und ein effizienter Pfad durch den Graph wäre dann nur von der Anzahl der durchlaufenen Kanten abhängig gewesen. Der effizienteste Pfad von A nach E ist nun (A, F, C, G, E).

Abbildung 4

SQL-Graph-DB

SQL-Graph-Datenbanken sind im SQL Server keine eigne Datenbankklasse, sondern nur eine spezielle Art von Tabellen. Diese werden in einem eigenen Ordner, „Graph-Tabellen“, im Management Studio angezeigt. Wie man diese Tabelle definiert, wird im folgenden Kapitel beschrieben.

Aufbau einer SQL-Graph-DB

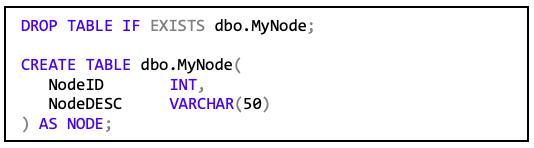
Um das Modell aus Abbildung 3 zu beschreiben baut man hierzu erst eine Knotentabelle auf. Grundsätzlich ist die Syntax die gleiche wie in den bisherigen Tabellendefinitionen allerdings mit dem Zusatz „AS NODE“ am Ende.

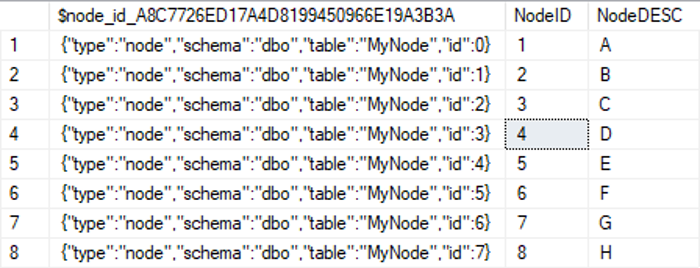
Anschließend befüllt man die Tabelle mit den Daten.

Mit einer normalen „SELECT *“-Anweisung auf die Tabelle ist zu erkennen, dass eine zusätzliche Spalte in der Tabelle existiert, welche gar nicht definiert wurde. Diese Spalte wurde vom SQL Server erstellt und wird auch automatisch verwaltet. Der String in dieser Spalte dient für den SQL-Server dazu, Knoten in größeren Graphen über mehrere Tabellen hinweg eindeutig zu identifizieren.

Abbildung 5

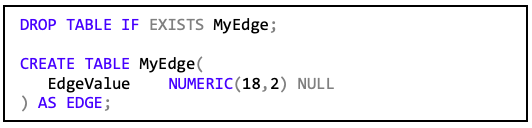
Das Skript für die Kantentabelle ergibt sich folgendermaßen:

Der Zusatz „AS Edge“ signalisiert für den SQL Server, dass es sich um eine Kantentabelle handelt. Wenn man nun Daten einfügt, …

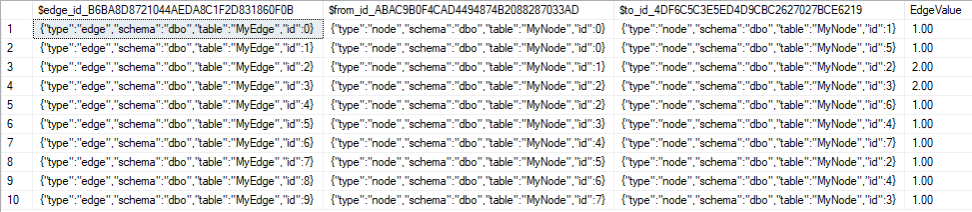
… dann kann man im Ergebnis sehen, dass auch in der Kantentabelle eine Identitätsspalte für jede Kante dazugekommen ist. Zusätzlich hat der SQL Server automatisch, für einen gerichteten Graphen, eine „from_id“ und eine „to_id“ Spalte für die zwei Knoten am Anfang und Ende jeder Kante eingefügt. Beim Einfügen muss man dann diese zwei Spalten befüllen, um die Kanten zu beschreiben, deshalb die INNER JOIN mit der Tabelle „MyNode“.

Abbildung 6

Erste Abfragen auf dem SQL-Graph

Im Folgenden analysieren wir auf dem Graphen Wege, wobei die Gewichtung des Weges durch die Kosten keine Rolle spielt. Die Gewichtung betrachten wir erst im nächsten Kapitel.

Abbildung 7

Alle Nachfolger eines Knoten

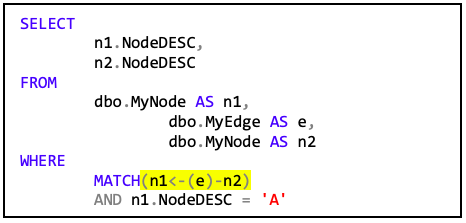
Zum Analysieren von Graphen stellt der SQL Server eine neue Syntax bereit. Man kann im folgenden Code erkennen, dass in der WHERE-Klausel die Verknüpfung zwischen der Knotentabellen n1 und n2 mit Hilfe der Kantentabelle e erstellt wird. Die Notation x-(y)->z stellt durch den Pfeil „->“ immer eine Richtung dar.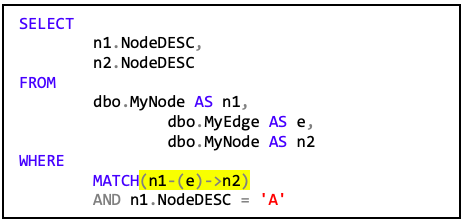

Somit ergibt sich aus der Abfrage mit umgedrehtem Verlauf…

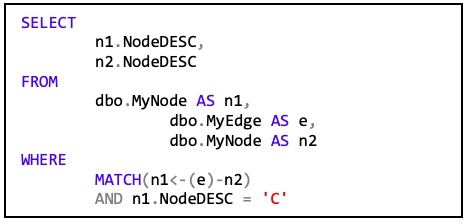
…kein Ergebnis, da es keine Kante gibt, die zu „A“ hinzeigt. Wenn man allerdings anstatt des Startknotens „A“ den Knoten „C“ wählt, …

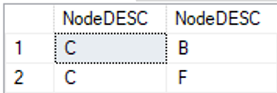
… dann ergibt sich folgendes Ergebnis:

Abbildung 8

Alle kürzesten Pfade, beliebiger Länge, ohne Wiederholung

Bisher haben wir nur Pfade der Länge 1 betrachtet, also direkte Nachfolger oder Vorgänger. Würde man mit der „MATCH“-Funktion weiterarbeiten, müsste man für jeden weiteren Schritt eines Pfades manuell diesen als JOINS aus Knoten- und Kantentabelle editieren. Das macht wenig Sinn und deshalb gibt es seit dem SQL Server 2019 die Funktion „SHORTEST_PATH“. Mit dieser Funktion ist es möglich, Pfade beliebiger Länge im Graphen zu suchen. Wie der Name schon signalisiert, werden durch die Funktion keine Schleifen betrachtet bzw. ausgegeben.

Im folgenden Code sieht man die Syntax für die „SHORTEST_PATH“-Funktion, diese steht innerhalb der MATCH-Funktion. Die „SHORTEST_PATH“-Funktion muss am Ende immer angeben, wie weit der Graph durchsucht werden soll. Ein „+“ gibt an, dass der komplette Graph durchsucht werden soll.

Die Tabellen e und n2 müssen mit dem Zusatz „FOR PATH“ angegeben werden und es stehen für die Pfadanalyse einige Aggregationsfunktionen bereit, wie hier die Funktion „STRING_AGG“ um die Knotennamen zu konkatenieren. Weitere Aggregate sind:

• STRING_AGG
• LAST_VALUE
• SUM
• COUNT
• AVG
• MIN
• MAX

Der Output des Skripts für den Graphen lautet dann wie folgt:

Abbildung 9

Erweiterte Analysen

Abbildung 10

Pfad mit Kosten

Bisher hat man alle Pfade anhand von Schritten bewertet. Die Funktion „SHORTEST_PATH“ hat dabei nicht die Werte „EdgeValue“ zur Ermittlung des kürzesten Pfades betrachtet, sondern nur die Anzahl an Schritten im Graph.

Leider bietet der SQL Server bis jetzt noch keine OnBoard-Funktionalität, um das Problem zu lösen, sondern man muss sich mit ein wenig Programmierarbeit behelfen. Die Funktion „SHORTEST_PATH“ hilft dabei, da es ohne diese Funktion sehr schwierig wäre, alle Pfade mit Auslassen von Schleifen zu betrachten.

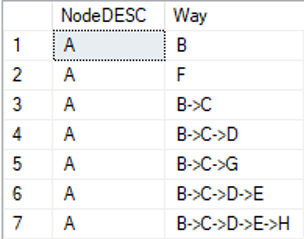
Zuerst erzeugt man deshalb eine Hilfstabelle, um alle Kosten zwischen allen Knotenkombinationen zu ermitteln. Eine Hilfstabelle ist notwendig und keine CTE, da in der bisherigen SQL-Server-Version die Funktion SHORTEST_PATH nicht innerhalb von CTE verwendet werden kann.

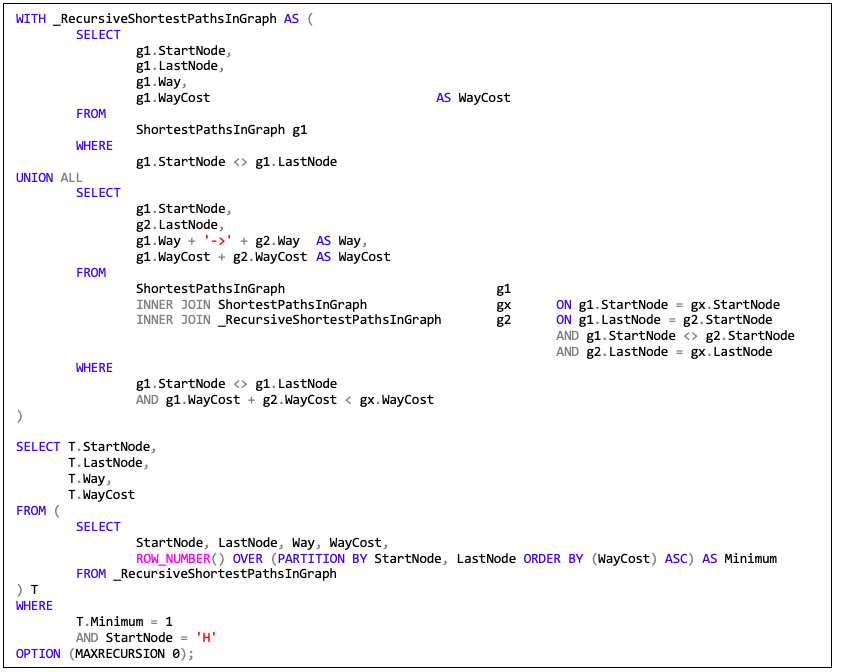
Anschließend wird die Tabelle „ShortestPathsInGraph“ rekursiv in einer CTE aufgerufen, um alle aus der „Shortest_Path“-Funktion stammenden Wege gegen jeden Teilweg mit den geringsten Kosten zu vergleichen.

Abbildung 11

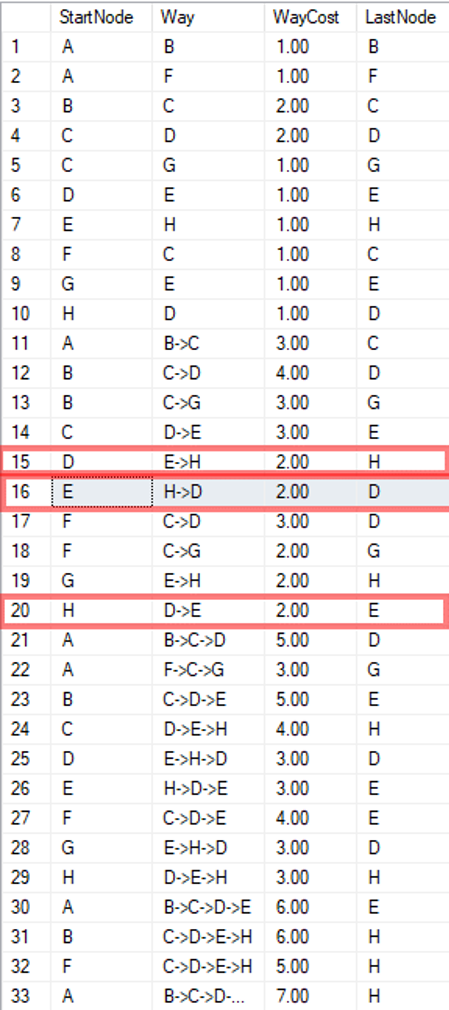
Im Output erkennt man dann, dass zwar die „Shortest_Path“-Funktion selbst Schleifen ausschließt, aber die Kombination aus den Teilwegen 15, 16 und 20 jeweils eine Schleife bilden kann. Im weiteren Verlauf muss deshalb darauf geachtet werden, dass hierdurch keine unendliche Tiefe entsteht.

In Zeile 29 ist zusätzlich ein Teilweg entstanden, bei dem sowohl der Anfangs- als auch der Endknoten identisch ist. Auch das muss bei zukünftiger Verwendung eliminiert werden.

Hieraus ergibt sich dann folgendes rekursive Skript zur Ermittlung von den Wegen mit den geringsten Kosten und Ausgangsknoten A.

Abbildung 12

Zusammenfassung

Dieser Blogbeitrag hat aufgezeigt, was Graphen-Datenbanken sind und wie Microsoft diese behandelt. Da diese Technologie im SQL Server noch neu ist, sind unterstützende Funktionen noch ein wenig dürftig und es ist zu hoffen, dass die Funktionspalette noch ausgebaut wird. Aber schon heute lassen sich Problemstellungen lösen (Kürzeste-Wege-Problem, Breiten- und Tiefensuche), welche mit relationalen Komponenten aufwendig zu realisieren sind, vor allem wenn der Graph Schleifen enthält oder Wege unterschiedliche Kosten aufweisen.