Rollierende Durchschnitte dienen im Normalfall dazu, stark schwankenden Werten mit einfachen Mitteln eine geglättete Entwicklung zu entlocken und damit ggf. Trends besser sichtbar zu machen.
Gerade wenn dies inhaltlich anhand der konkreten Daten plausibel erscheint, so muss der DeltaMaster-Anwender hier sofort die Chance auf die Berechnung einer Abweichung erkennen und sich damit – insbesondere auch im Umfeld prototypischer DeltaMaster-Anwendungen – weitere Analysemöglichkeiten eröffnen.
Auf allen Datenbanken, die von DeltaMaster per MDX angesprochen werden können, wird die Option für gleitende Durchschnitte über den Zeitanalyseelement-Assistenten per Mausklick angeboten. In der Praxis werden gleitende Durchschnitte insbesondere dafür verwendet, um bei relativ stark schwankenden Tages- oder Monatswerten einen Indikator dafür zu erhalten, was denn über die „letzte Zeit“ ein typischer, quasi ein „zu erwartender Wert“ war. Die Glättung, die hier erzielt wird, hat natürlich immer den Nachteil, dass Trends erst mit einer gewissen Verzögerung sichtbar werden, da ältere Werte ggf. neuere (Teil-)Trends noch überlagern können.
Dennoch gibt es ein paar gute Argumente, warum gleitende Durchschnitte in bestimmten Anwendungsfeldern als Referenzgrößen herangezogen werden können. Und wenn dies möglich ist, so wird der erfahrene DeltaMaster-Anwender natürlich sofort die Gelegenheit nutzen, um diese Referenzwerte nicht nur in seinen Berichten darzustellen, sondern sie auch mathematisch in eine berechnete Abweichung zu integrieren. Denn damit ergibt sich eine neue Form eines berechneten Deltas, das sich mit den zahlreichen DeltaMaster-Methoden auf seine Zusammensetzung hin analysieren lässt. Und wieder findet sicht damit ein Anwendungsfall, der praxisrelevant und zugleich sehr spezifisch für DeltaMaster ist, sich dagegen aber von anderen Tools wird schwerlich realisieren lassen.
Nicht zuletzt lässt sich diese Form von „Referenzwertgenerierung“ auch sehr gut für die Aufwertung von DeltaMaster-Prototypen nutzen, in denen evtl. weder Planwerte noch sonstig geartete Referenzwerte identifizierbar sind. Sofern aber die Historie der Werte ausreichend umfangreich ist, so lassen sich über den Kniff mit den rollierenden Durchschnitten inhaltliche Aussagen aus diesen Deltas ableiten, die potenzielle Interessenten aufhorchen lassen werden.
Wann kann ein Vergleich mit einem rollierenden Durchschnitt sinnvoll sein?
Nicht in jedem Fall ist die Verwendung eines rollierenden Durchschnitts aus fachlicher Sicht zu rechtfertigen. So wird es bei einer rein monatlichen Betrachtung von Finanzgrößen, die aufgrund kontinuierlichen Wachstums des Unternehmens ebenfalls mehr oder minder stetig steigen, sicherlich keinen Sinn machen, einen „hinterherhinkenden“ gleitenden Durchschnitt als Vergleich heranzuziehen. Dagegen kann es in einer operativen Umgebung (Produktion, Service, Lager, Transport), die im Tagesrhythmus überwacht wird, durchaus plausibel sein, die eher stochastischen Schwankungen bei z.B. Auftragseingängen, Qualitätsmessungen oder Kommissioniermengen durch eine Betrachtung der rollierenden Durchschnitte geglättet zu betrachten. Gerade in solchen operativen Umgebungen kann auch davon ausgegangen werden, dass sich das entsprechende System an ein gewisses „Durchschnittsniveau“ der Auslastung anpasst. Mit anderen Worten: Nur bei mittelfristigen Niveauveränderungen wird sich auch das Produktions-/Lager-/Servicesystem als Ganzes anpassen, indem die Organisation verändert, mehr oder anderes Personal eingesetzt und die Maschineneinsatzplanung verändert wird. Wenn sich jedoch kurzfristig die Rahmenbedingungen ändern und damit vom „Durchschnittsniveau“ abweichen, so kann diese Abweichung ein interessanter operativer Indikator für das Management sein, den es näher zu untersuchen gilt.
Wann ein rollierender Durchschnitt plausibel anwendbar sein kann, lässt sich damit grob anhand der folgenden Hinweise prüfen:
- Die Zeitintervalle der betrachteten Daten sind eher kürzerer Natur
Beispiel: tagesbasierte Daten werden betrachtet
- Die betrachteten Faktenwerte haben eine deutlich stochastische Verteilung über die Zeit (zumindest im zu analysierenden Zeitintervall)
Beispiel: Auftragseingänge, die über einzelne Tage eines Monats schwanken, aber keine systematischen Schwerpunkte (z.B. immer Montags wenig Eingänge) zeigen
Sind in einer Sequenz von Werten jedoch systematische Muster enthalten, so werden diese durch den rollierenden Durchschnitt latent eher verdeckt, was eventuell nicht gewollt ist. Ist das Muster jedoch bekannt, so kann eventuell dennoch sinnvoll ein gleitender Durchschnitt genutzt werden: Gibt es z.B. bekannte Saisonalitäten, die zu berücksichtigen sind und sollen diese sichtbar gemacht werden, so muss der rollierende Durchschnitt zumindest „über die Saison hinaus“ definiert werden, damit er als „mittleres Normalmaß“ dienen kann und die Deltas dann die Saisonalität erkennen lassen.
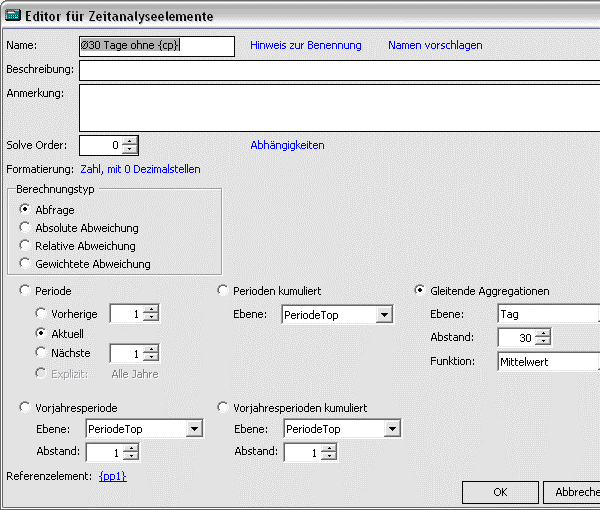
Für DeltaMaster-Nutzer erwähnenswert: Über das „Referenzelement“ kann gesteuert werden, ob evtl. die aktuellsten Werte unberücksichtigt bleiben sollen – also z.B. ein {ppX-Element} als Basis genutzt wird. Ebenso kann – falls historisch rückblickend analysiert wird – auch ein „zukünftiger“ Wert in Bezug auf die aktuelle Sicht als Referenzelement genutzt (dann sind ja auch „Zukunftswerte“ bereits vorhanden) und damit die Zusammensetzung des rollierenden Durchschnitts im Detail weiter beeinflusst werden.
Worauf ist bei der Berrechnung der rollierenden Durchschnitte und Abweichungen zu achten?
In vielen Fällen wird der Vergleich mit einem „historischen Durchschnitt“ so aussehen, dass der aktuelle Wert natürlich noch nicht im „historischen Durchschnitt“ enthalten sein soll. In dem Fall muss bei der Definition des Zeitanalyseelements auf die entsprechende Einstellung eines passenden Referenzelements geachtet werden. Im Beispiel unten ist dies das Element {pp1}
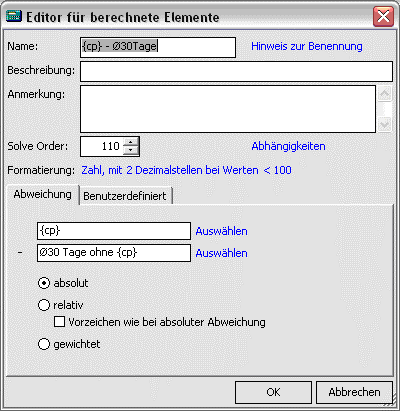
Um das Delta vom aktuellen Wert zum rollierenden Wert zu definieren, kann in DeltaMaster der Standarddialog für berechnete Elemente genutzt werden. Bei der Definition sollte jedoch unbedingt die SolveOrder geprüft werden, vor allem dann, wenn dieses Zeitanalyseelement auf berechnete Kennzahlen angewendet werden soll. Sowohl absolute wie relative Abweichungen zum rollierenden Durchschnitt sind sinnvolle Berechnungen, die im Einzelfall inhaltlich zu bewerten sind (vgl. unten das Beispiel).
Beispiel für eine Abweichungsanalyse mit rollierenden Durchschnitten
Das folgende Beispiel ist dem Blogbeitrag „Lagerlogistik-Beispiel für Pre-Sales-Einsatz“ entnommen. Dort geht es um die Bewertung der aktuell zu bearbeitenden Aufträge, d.h. die Bedingungen (s.o.) sind beide erfüllt: die betrachtete Zeitperiode ist jeweils recht kurz und die stochastische Verteilung eingehender Aufträge kann als gegeben angenommen werden.
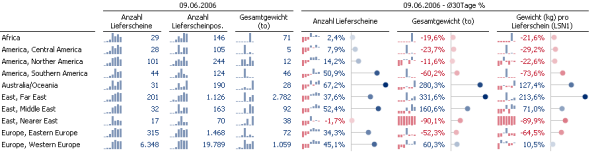
Für die Personaleinsatzplanung im beispielhaft betrachteten Lager ist immer dann besondere Aufmerksamkeit geboten, wenn sich der Auftragsmix hinsichtlich Anzahl, Gewicht u.ä. Charakteristika verändert. Da jedoch eine Veränderung zu einem Vortag oder zu einem Vormonat an sich keine sinnvolle Indikation hinsichtlich „regulär“ vs. „irregulär“ erlaubt, wird ein rollierender 30-Tage-Durchschnitt als Referenz herangezogen. Unter der Annahme, dass sich die Lagerprozesse auf längerfristige Rahmenbedingungen, wie sie durch den 30-Tage-Durchschnitt dargestellt sind, einschwingen, so stellen deutliche Abweichungen von diesem Durchschnitt vermutlich ein Problem für den aktuellen Lagerprozess dar. In diesem Sinne weisen z.B. die deutlichen Abweichungen in „East, Far East“ auf eine notwendige Prozessanpassung (z.B. verstärkten Personaleinsatz zur Vorbereitung von umfangreichen Zollpapieren) hin. Die Abweichung zum 30-Tage-Durchschnitt wird explizit ausgerechnet und ausgewiesen.
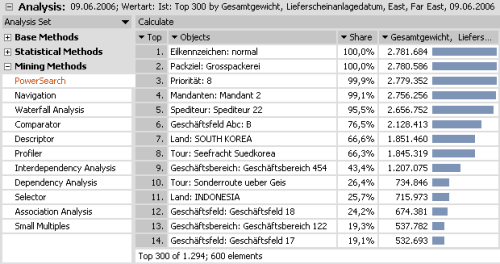
Mithilfe des PowerSearch-Verfahrens lässt sich mit einer Drag-and-Drop-Aktion eine umfangreiche Ursachenanalyse für diese Abweichung identifizieren. Wobei hier nicht die Abweichungszahl an sich, sondern die zugehörige Basiskennzahl (z.B. Gesamtgewicht für den aktuellen Tag) in das Verfahren als Parameter eingehen sollte, um den tatsächlichen Auftragseingang des betreffenden Tages (also wie viel Gewicht faktisch zu verarbeiten sein wird) zu analysieren. Die Abweichung dient in der tabellarischen Darstellung lediglich als Indikator für die Identifikation der kritischen Region. Im Ergebnis zeigt sich, dass insbesondere Südkorea, aber auch Indonesien die Zielländer dieser großen Aufträge sind. Spediteur 22 sollte vermutlich vorgewarnt werden und für die Seefracht lassen sich bereits administrative Prozesse anstoßen. Da alles in der Großpackerei verpackt werden soll, ist dort ausreichend Personal vorzuhalten, um diese Aufträge zeitgerecht abarbeiten zu können.
Dieses Beispiel verdeutlicht, dass der Vergleich mit einem rollierenden Durchschnitt einen praktikablen Hinweis auf notwendige Aktionen liefern kann. Technisch wird DeltaMaster zur Berechnung dieses Vergleichs und zur Erklärung der Abweichung herangezogen.