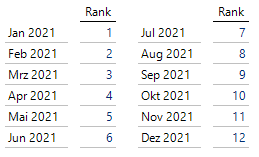In der simplen Rangfolge steckt überraschend viel analytische Kraft für das Controlling: Die Sortierung zeigt die Bedeutung, Abstände werden klar, sogar die Verteilung ist zu erkennen, und all das in einer gut verständlichen Darstellung. DeltaMaster berechnet und präsentiert Rangfolgen automatisch – oder visualisiert die Ergebnisse von individuellen MDX-Abfragen, hier: mit der RANK-Funktion.
Rank in der Theorie
Das Know-how über die Funktionsweise der Rank-Funktion gehört zum Fundament eines jeden erfahrenen Datenanalysten und ist in heutigen Projekten mittlerweile ein häufig genutzter Ansatz, um dem Berichtswesen sinnvolle Erweiterungen zu geben.
Zunächst wird auf die Grundlagen der Rank-Funktion eingegangen. Hierfür wird die Microsoft-MDX-Funktionsreferenz (Rank (MDX)) aufgegriffen. Microsoft beschreibt das Verhalten der Funktion folgendermaßen: „Returns the one-based rank of a specified tuple in a specified set.“
Diese Beschreibung ist Microsoft-typisch kurz, trifft den Nagel aber trotzdem auf den Kopf. Im Folgenden soll die Funktion im Detail untersucht werden, denn wie bei den meisten Funktionen gibt es auch hier ein paar Fallstricke, über die man möglicherweise stolpern kann. Die Syntax der Funktion lautet:
Rank(Tuple_Expression, Set_Expression [ ,Numeric Expression ] )
Die Rank-Funktion setzt sich aus drei Parametern zusammen:
- Das erste Argument erwartet einen Tupelausdruck und ist der zu bewertende Ausdruck in der Funktion.
- Das zweite Argument erwartet einen Mengenausdruck und gibt den Umfang der zu bewertenden Ausdrücke an.
- Das dritte Argument erwartet einen numerischen Ausdruck und bestimmt die Ordnungszahl des jeweiligen Ausdrucks.
Das dritte Argument ist ein optionales Argument und muss nicht zwangsläufig mit übergeben werden. Wird dieses Argument ausgelassen, wird die Rangfolge über die Sortierung der übergebenen Menge ermittelt. Was dies im Detail bedeutet, wird im Abschnitt „Ich bin der Beste – aber in was?“ genauer erläutert.
Rank in der Praxis
Dieser Abschnitt umfasst die Verwendung der Rank-Funktion in der Praxis anhand von Beispielen auf der Referenzdatenbank „Chair“.
Der Normalfall – Ranking nach einem numerischen Ausdruck
Im ersten Beispiel wird eine Rangfolge über die Produktgruppe aus der Dimension Produkt erstellt. Dazu wird ein benutzerdefinierter Analysewert erstellt und der folgende Code in die Definition eingefügt:
RANK ([Produkt].[Produkt].CurrentMember
,[Produkt].[Produkt].[Produktgruppe]
,[Measures].[Umsatz])Als Tupelausdruck wird in diesem Beispiel das CurrentMember der aktuellen Hierarchie verwendet, sodass die Rangfolge dynamisch für jede übergebene Produktgruppe ausgewertet wird. Die vollständige Ebene der Produktgruppe wird als Mengenausdruck verwendet, sodass die Rangfolge über alle Produktgruppen ausgewertet werden soll.
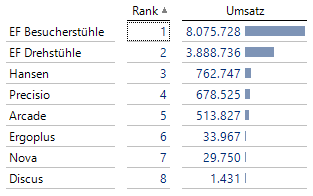
Als numerischer Ausdruck wird der Umsatz verwendet, sodass die Rangfolge durch dessen Wert bestimmt wird. Verwendet man diese Kennzahl in einem Bericht und kombiniert dies mit der Produktgruppe, so erhält man für jede Produktgruppe die Ordnungszahl entsprechend des Umsatzes.
Abb. 1: aufsteigende Rangfolge nach Umsatz je Produktgruppe
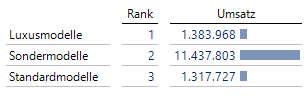
Benötigt man an dieser Stelle jedoch keine aufsteigende Rangfolge, sondern ist eine absteigende Sortierung gefragt, lässt sich dies mit einem einfachen Kniff lösen. Hierzu wird als numerischer Ausdruck der Rabatt gewählt und die Rangfolge über die Produktgruppen soll absteigend entsprechend des Rabattes bewertet werden.
Da für den Rabatt eine invertierte Rangfolge benötigt wird, multipliziert man den numerischen Ausdruck bei der Übergabe an die Rank-Funktion mit „-1“:
RANK([Produkt].[Produkt].CurrentMember
,[Produkt].[Produkt].[Produktgruppe]
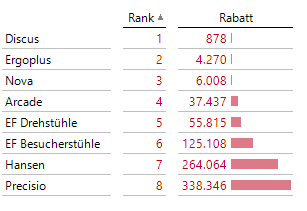
,[Measures].[Rabatt] * -1)Als Ergebnis erhält man eine absteigende Rangfolge der Produktgruppen nach der Höhe des Rabattes:
Abb. 2: absteigende Rangfolge nach Rabatt je Produktgruppe
Äpfel und Birnen – bitte nicht!
Im vorigen Abschnitt haben wir kennengelernt, wie sich die Rank-Funktion innerhalb einer kompletten Ebene verhält. Wird die Anforderung vielschichtiger und die Rangfolge soll abhängig von den jeweiligen Hierarchiegruppen abgebildet werden, muss der MDX-Codebaustein entsprechend angepasst werden.
Hierzu verändern wir den Mengenausdruck und verwenden folgenden MDX-Code:
RANK([Produkt].[Produkt].CurrentMember
,[Produkt].[Produkt].CurrentMember.Siblings
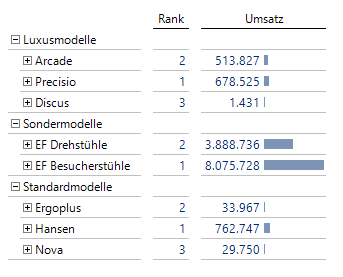
,[Measures].[Umsatz])Der Siblings-Befehl gibt die gleichgeordneten Elemente des aktuellen Elements zurück und schließt das aktuelle Element ein. Das Ergebnis sieht wie folgt aus:
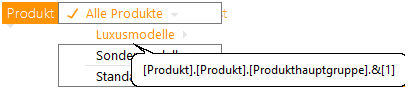
Abb. 3: Rangfolgen innerhalb der Hierarchiegruppen
Um die Rangfolge besser nachvollziehen zu können, wurden zu Vereinfachungszwecken die jeweiligen Produkthauptgruppen eingeblendet. Es lässt sich wunderbar erkennen, dass die Rangfolgen nur innerhalb der jeweiligen Hierarchiegruppen gebildet werden. Eine großartige Möglichkeit, um zu verhindern, dass Äpfel mit Birnen verglichen werden.
Noch mehr Äpfel und noch mehr Birnen – oje!
Um das bereits Untersuchte auf die Spitze zu treiben, wird der folgende Anwendungsfall herangezogen. Oft ist es notwendig, dass dimensionsübergreifende Vergleiche notwendig sind. So könnte eine Anforderung lauten, dass eine Rangfolge für jedes Produkt eines jeden Kunden gebildet werden soll.
Für die Berechnung der Rangfolge wird der folgende MDX-Code verwendet:
RANK(([Kunde].[Kunde].CurrentMember, [Produkt].[Produkt].CurrentMember)
,[Kunde].[Kunde].CurrentMember * [Produkt].[Produkt].[Produktgruppe]
,[Measures].[Umsatz])Der Tupelmengenausdruck ist das CurrentMember aus beiden Hierarchien, im vorliegenden Fall aus der Kunden- und Produktdimension. Als Mengenausdruck wird das Kreuzprodukt aus dem CurrentMember der Kundenhierarchie und der vollständigen Produktgruppenebene der Produkthierarchie verwendet.
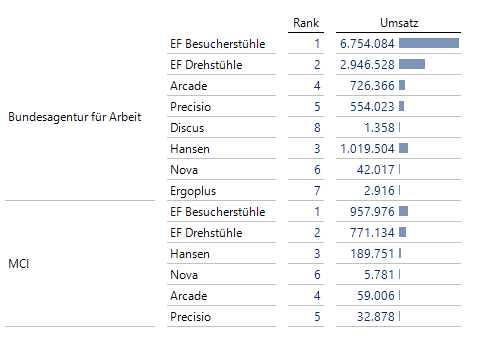
Diese beiden Ausdrücke unterscheiden sich wesentlich zum vorherigen Beispiel. Als Ergebnis erhalten wir die Ordinalzahl der Produkte des jeweiligen Kunden:
Abb. 4: Ordinalzahl der Produkte des jeweiligen Kunden
Ich bin der Beste – aber in was?
Die bisher untersuchten Beispiele wurden immer nach einem numerischen Ausdruck ausgewertet. Doch wie verhält sich die Rank-Funktion, wenn kein numerischer Ausdruck verwendet wird? Wir erinnern uns: Der numerische Ausdruck ist optional.
Diese Frage lässt sich ganz einfach beantworten: Wenn kein numerischer Ausdruck verwendet wird, basiert die Reihenfolge auf der Sortierung der übergebenen Menge. In diesem Beispiel wird der folgende MDX-Code für die Berechnung der Rangfolge verwendet:
RANK([Produkt].[Produkt].CurrentMember
,[Produkt].[Produkt].[Produkthauptgruppe])Der numerische Ausdruck wird ausgelassen und das Ergebnis ist Folgendes:
Abb. 5: Rangfolge
Es stellt sich jetzt jedoch die Frage, was die Sortierung der übergebenen Menge beeinflusst. Auch das lässt sich einfach erklären: Auf oberster Ebene wird immer die Reihenfolge der technischen Schlüssel der jeweiligen Elemente verwendet. In unserem Beispiel haben die Produkthauptgruppen durchnummerierte numerische Schlüssel.
Abb. 6: Schlüssel der Produkthauptgruppen
Auf darunterliegenden Ebenen sind die Elemente wiederum nur innerhalb der eigenen Hierarchiegruppe sortiert, was wiederum bedeutet, dass der Aufbau der Hierarchie die Sortierung der Menge beeinflusst. Wer möchte, der kann die Sortierung der Menge vor Übergabe an den Mengenausdruck auch nach Belieben sortieren.
Cheat Sheet
In diesem abschließenden Kapitel wird noch auf einen Stolperstein hingewiesen und ein interessanter Codebaustein mit an die Hand geben.
Last but not least?
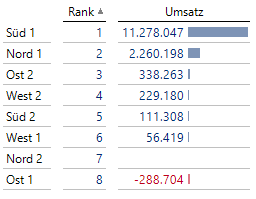
Nehmen wir an, dass eines der Gebiete keinen Umsatz ausgewiesen hat und ein weiteres Gebiet sogar einen negativen Umsatz hat. Die Erwartung wäre, dass eine Rangfolge über die Gebiete nach dem Umsatz das erstgenannte Gebiet nicht berücksichtigt. Die Realität sieht jedoch anders aus:
Abb. 7: Rangfolge mit leerer Zeile
Das Gebiet „Ost 1“ ist wider Erwarten nach dem Gebiet „Nord 2“ platziert, obwohl dieser wiederum gar keinen Umsatz ausgewiesen hat. Schaut man sich jedoch die eingangs erwähnte Funktionsbeschreibung seitens Microsoft an, deckt sich dies mit dem erwähnten Verhalten. Die Menge ist in diesem Fall nämlich die vollständige Ebene der Gebiete der Kundendimension. Leere Elemente werden in der Rank-Funktion wie „0“-Werte behandelt, wodurch es zu dieser Darstellung kommt.
An dieser Stelle wäre es sinnvoller, nur nichtleere Elemente der Ebene zu berücksichtigen. Das lässt sich mit folgendem MDX-Code einfach realisieren:
RANK([Kunde].[Kunde].CurrentMember
,NONEMPTY([Kunde].[Kunde].[Gebiet],[Measures].[Umsatz])
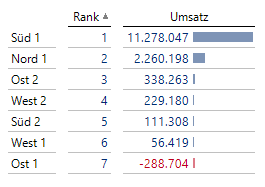
,[Measures].[Umsatz])Das Ergebnis ist eine saubere Rangfolge ohne Berücksichtigung von umsatzlosen Gebieten:
Abb. 8: Rangfolge ohne leere Zeile
Wann bin ich?
Ein weiterer interessanter Anwendungsfall ist die Ermittlung von Ordinalzahlen der jeweiligen Monate eines bestimmten Jahres. Mit folgendem MDX-Code lässt sich die Rangfolge über die Monate berechnen:
RANK([Periode].[Periode].CurrentMember
,DESCENDANTS(
ANCESTOR([Periode].[Periode].CurrentMember
,[Periode].[Periode].[Jahr])
,[Periode].[Periode].[Monat]))Als Ergebnis erhält man die Ordinalzahl entsprechend des jeweiligen Monats:
Abb. 9: Rangfolge nach Monaten
Auf Basis dieser Rangfolge lassen sich jetzt beispielsweise einfache Durchschnitte über die Monate hinweg bilden.