Viele Planungsprojekte von Kunden sollen automatisch mit Vorschlagswerten befüllt werden, bevor die Anwender mit der eigentlichen Planung beginnen. Diese Vorschläge hängen häufig proportional mit vorangegangenen Planwerten zusammen. Wie solche Vorschlagswerte als ganze Zahlen mit SQL verteilt werden können, ohne dass in Summe ein Rundungsfehler entsteht, zeigt der folgende Beitrag. Hierbei wird auch auf mögliche Zusatzbedingungen und Erweiterungen sowie Limitationen des Ansatzes eingegangen.

Grundproblem und Lösung

Um das Problem zu skizzieren, wird von folgendem Szenario ausgegangen:
Die Planwerte für die Produktion des nächsten Jahres sollen vorbefüllt werden.

Gegeben sind:

• Planzahlen pro Produkt und Monat der letzten Planungsrunde und
• Planzahlen pro Produkt für die aktuelle Planungsrunde auf Jahresebene.

Gesucht wird die Verteilung der Produktion auf die Monate (möglichst proportional zur letzten Planungsrunde), wobei die Produktion in Summe dem Jahreswert entsprechen muss. Mit SQL ist das relativ einfach über einen Dreisatz zu lösen.

Allerdings gilt folgende Bedingung: Es dürfen nur ganze Einheiten geplant werden können.

Das macht die Verteilung komplizierter, da man nicht davon ausgehen kann, dass die durch den Dreisatz errechneten Werte ganzzahlig sind oder die gerundeten Werte in Summe korrekt sind.

Vorbereitung der Daten

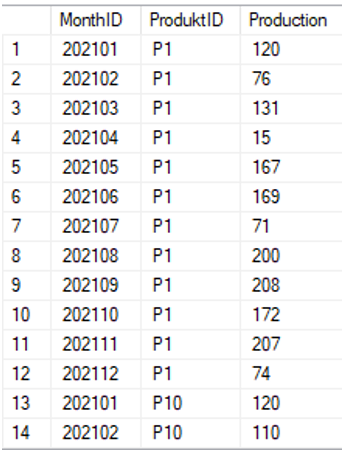
Zunächst werden die Daten gesichtet und miteinander so verknüpft, dass alle relevanten Informationen zur Verfügung stehen. Im vorliegenden Szenario liegen die Daten in zwei unterschiedlichen Tabellen. Die Verteilung der letzten Planungsrunde befindet sich in einer Tabelle (vgl. Abbildung 1).

Abbildung 1: Verteilung der letzten Planungsrunde

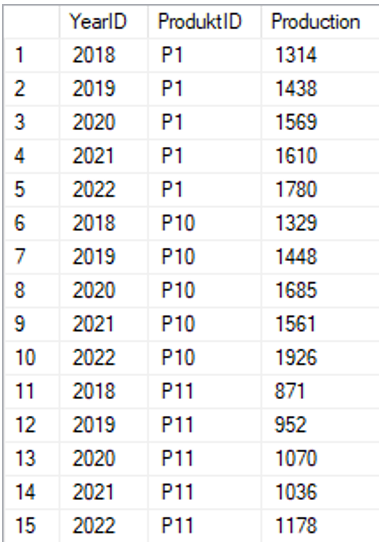
Die Summen auf Jahresebene befinden sich in einer anderen Tabelle (vgl. Abbildung 2).

Abbildung 2: Planungssummen auf Jahresebene

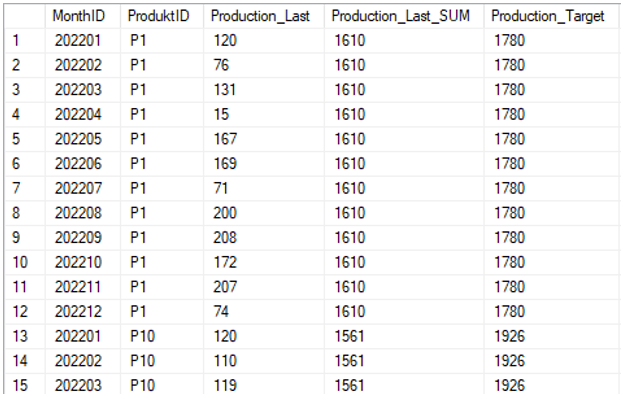
Diese Tabellen können nun mit Hilfe von Joins miteinander verknüpft werden (vgl. Abbildung 3).

Abbildung 3: Alle Input-Werte in einer Tabelle

Bei dieser Verknüpfung wurden die Monatswerte bereits auf das nächste Jahr verschoben. Es stehen nun in jeder Zeile die Jahressummen der letzten Planungsrunde (Production_Last_SUM) und der vorzubefüllenden Runde (Production_Target) zur Verfügung

Anwendung des Dreisatzes

Als erster Schritt wird der eingangs erwähnte Dreisatz durchgeführt. Die neue, ungerundete Produktion wird gemäß der folgenden Formel berechnet:

Production_new_unrounded = Production_Target / Production_Last_SUM * Production_Last

Hierbei ist zu beachten, dass mindestens einer der Werte zu einem Float- oder Decimal-Datentypen konvertiert wird, da reine Integer-Divisionen nicht das gewünschte Gleitkommaergebnis liefern würden.

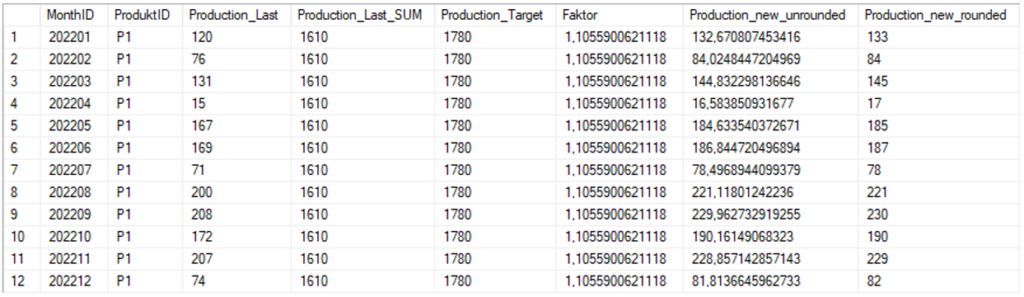
Nach zusätzlicher Rundung ergibt sich das Ergebnis wie in Abbildung 4 dargestellt.

Abbildung 4: Ergebnis nach Dreisatz

Ermittlung des Rundungsfehlers

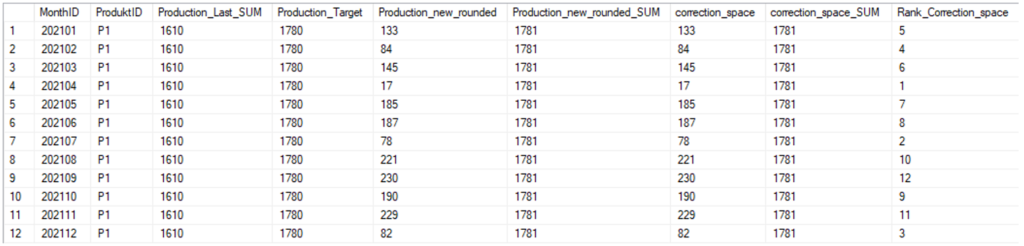
Um prüfen, wo die Werte korrigiert werden müssen,  wird zunächst auf Rundungsfehler geprüft. Hierfür werden die berechneten, gerundeten Werte aufsummiert und mit dem Zielwert verglichen. Das ist an dieser Stelle mit Hilfe von SQL-Window-Functions sehr einfach zu realisieren. Um im Anschluss den Code so generisch wie möglich zu halten, wird die Differenz aufgeteilt in Vorzeichen (SIGN) und Betrag (ABS). Das Ergebnis lässt sich der Abbildung 5 entnehmen.

Abbildung 5: Berechnung des Rundungsfehlers

In diesem einfachen Beispiel kann der Rundungsfehler per Definition nicht größer werden als 11. Dies muss aber nicht immer der Fall sein, wenn weitere Nebenbedingungen einschränkend wirken. Daher sollte der Code an dieser Stelle auch so generisch wie möglich sein und unter allen Voraussetzungen funktionieren.

Ermittlung des verfügbaren Platzes für Korrekturen

Es wird nun der theoretisch verfügbare Platz berechnet, der für Korrekturen zur Verfügung steht. Im vorliegenden Fall entspricht dieser für negative Abweichungen genau dem gerundeten Ergebnis, da wir davon ausgehen, dass die Produktion nicht unter „0“ fallen darf. Für positive Abweichungen gibt es keine Obergrenze, allerdings sollte die Proportionalität gewahrt bleiben. Es bietet sich daher an, die gerundeten Werte multipliziert mit dem Zielwert des Jahres zu verwenden. So wird selbst für den Extremfall, dass nur ein Monat gefüllt werden kann und dieser mit 1 befüllt ist, der komplette Zielwert erreicht. Die Berechnung dieses Platzes für Korrekturen sollte idealerweise gekapselt werden, z. B. in einem Cross Apply, da zusätzlich zu dem Wert auf Monatsebene auch noch der Jahreswert und die Row Number per Window-Function ermittelt wird (vgl. Abbildung 6).

Abbildung 6: Platz für Korrekturen

Verteilung des Rundungsfehlers

All diese Berechnungen konnten bisher im gleichen Schritt durchgeführt werden. Ab jetzt werden per Window-Functions berechnete Werte benötigt. Daher sollte spätestens hier mit mehreren Subselects/CTEs/Temp Tables gearbeitet werden.

Mithilfe der Ceiling-Funktion wird der Rundungsfehler proportional zum Platz für Korrekturen auf die Monate verteilt. Dies geschieht wieder mit Hilfe des Dreisatzes:

Rounding_error_roundUP = ⌈correction_Space / corrections_Space_SUM * rounding_error_ABS ⌉

Ceiling führt dazu, dass immer aufgerundet wird. So wird sichergestellt, dass der resultierende Fehler immer zwischen 0 und 11 liegt. Dies geschieht durch den Vergleich der Differenz der summierten aufgerundeten Werte und dem Fehler mit dem Rang des Platzes für Korrekturen. Ist der Rang kleiner als die Differenz, wird abgerundet.

Im vorliegenden Beispiel ist die Summe der aufgerundeten Korrekturen 12 und der errechnete Rundungsfehler 1. Das bedeutet, dass 12 – 1 = 11 Monate abgerundet werden müssen. Nur der Monat mit dem Rang 12 (der Monat mit dem größten Korrekturplatz) wird korrigiert. Diese errechnete Korrektur muss nur noch auf das gerundete Ergebnis unter Berücksichtigung des Vorzeichens aufaddiert werden.

Abbildung 7: Resultierende Korrektur

Auf Jahresebene stimmen die Werte bei bestmöglicher Berücksichtigung der Proportionalität mit der Vorgabe über ein.

Es ist zu beachten, dass diese Berechnung nur für Datensätze mit einem Platz für Korrekturen > 0 sinnvoll ist, da die anderen Datensätze nicht verändert werden dürfen. Die resultierende Produktion muss also durch eine Verknüpfung der Abfrage mit den gerundeten Werten und der Abfrage mit den Korrekturen errechnet werden.

Erweiterung der Problemstellung

Die bisher gezeigte Logik verwendet zwei proportionale Verteilungen. Das ist nicht zwingend notwendig. Es wäre auch möglich die gleiche Logik ohne die erste Vorbefüllung anzuwenden und direkt gemäß der Auf- und Abrundungslogik zu verteilen.

Allerdings ist es in der Praxis selten so, dass eine einfache Verteilung ausreichend ist. Meistens gibt es noch zusätzliche Bedingungen, die erfüllt werden müssen. Das eingangs beschriebene Szenario wird daher um eine weitere Zusatzbedingung erweitert:

Die Produktionskapazität von 200 Einheiten pro Produkt pro Monat darf nicht überschritten werden.

Dies ist eine vereinfachte Formulierung von Einschränkungen, die in der Praxis möglich sind. Die Komplexität dieser Einschränkungen kann sehr hoch sein und im Laufe der Zeit um immer mehr Bedingungen erweitert werden. Daher ist es ratsam, sich bereits bei der initialen Implementierung die Möglichkeit für Anpassungen offen zu halten.

Im vorliegenden Beispiel sind zwei Anpassungen notwendig:

1. Die initiale, proportionale Verteilung darf 200 nicht überschreiten.
2. Die Berechnung des Platzes für Korrekturen ergibt sich für positive Änderung jetzt aus 200 abzüglich der proportionalen Verteilung.

Wenn der bisherige Code gut gekapselt und strukturiert ist, müssen für so eine Änderung genau die-se zwei Berechnungen angepasst werden. Die Logik an sich bleibt dabei unverändert.

Das Ergebnis mit der zusätzlichen Bedingung stellt sich wie in Abbildung 8 dar.

Abbildung 8: Ergebnis mit Einschränkung der Produktionskapazität

In der Abbildung 8 lässt sich erkennen, dass die zusätzliche Einschränkung der Produktionskapazität in drei Monaten greift. Daraus ergibt sich ein sehr großer Rundungsfehler. Dieser kann aber über die verbleibenden neun Monate ausgeglichen werden.

Zusätzliche Anmerkungen

Das hier gezeigte Vorgehen kann problemlos auf andere Anwendungsfälle angewandt werden, bei denen Verteilungen notwendig sind.

Die Komplexität der Zusatzbedingungen ist prinzipiell nur die logische Machbarkeit begrenzt. Wenn die Zusatzbedingungen so gewählt sind, dass es eine Verteilung gibt, wird auch eine Verteilung errechnet.

Bei der Verteilung des Rundungsfehlers gemäß dem Platz für Korrekturen weicht der gezeigte Ansatz leicht von der Prämisse der proportionalen Verteilung ab, verzichtet dafür aber auf ein iteratives Vorgehen bei der Berücksichtigung der Zusatzbedingungen. Dies führt zu einer sehr guten Wartbarkeit und Nachvollziehbarkeit für den Anwender.