Das Thema Hochrechnungen, gerne auch als Prognose bezeichnet, ist eine häufig gestellte Anforderung an Unternehmensberichte. Dabei ist die Definition der Prognose meist individuell und stets den jeweiligen Gegebenheiten und Geschäftsmodellen unterworfen. Reicht es beispielsweise aus, für den Rest des laufenden Geschäftsjahres vorhandene Planwerte als Ziel anzunehmen? Oder ist für die Betrachtung eher der entsprechende Vorjahreswert von Interesse und aussagekräftiger? Unterliegt die Entwicklung wiederkehrenden Saisonalitäten? Das sind nur einige Fragestellungen, die es bei der kundenindividuellen Entwicklung einer Hochrechnung zu diskutieren und beachten gilt. Ein weiteres wichtiges Detail ist die Festlegung, ab wann sich der Berichtsempfänger datentechnisch in der Vergangenheit und wann in der Zukunft befindet?
Einen ersten Ansatz liefern wir mit dem DeltaMaster ab Version 5.5.8 bereits aus, den sogenannten „Way-to-Go“-Bericht. Dieser kann vollständig automatisiert mit Hilfe des Startassistenten auf (fast) jedem Datenmodell erstellt werden, vorhandene Planwerte vorausgesetzt. Allerdings basiert diese Form der Prognose auf der Fragestellung, was das Unternehmen im Verlauf des Jahres erreichen muss, um am Ende den Plan zu erfüllen.
In diesem Blogbeitrag zeigen wir einige Lösungsansätze mit Hilfe von DeltaMaster und ein wenig MDX, die es jedem Interessierten ermöglichen, die Aussage der Hochrechnung durch ein paar „Stellschrauben“ zu individualisieren. Am Ende soll eine Hochrechnung entstehen, die den Entscheidern zu jeder Zeit sagt, wo das Unternehmen am Jahresende stehen wird.
Als Basis dient die bekannte Demonstrationsdatenbank „Chair“. Diese beinhaltet neben den Umsatzzahlen der Jahre 2010 bis 2014 auch zugehörige Planumsätze. Für die verschiedenen Berechnungen legen wir einfach in der Stammdatentabelle der Dimension Wertart neue Elemente an, um später in einem Bericht die unterschiedlichen Ergebnisse gegenüberstellen zu können.
Abb. 1: neue Wertarten
Die Bezeichnungen sollen bereits einen ersten Aufschluss über die verwendeten Berechnungen geben. Widmen wir uns gleich der Berechnung der ersten Variante (HR1). Dies soll die einfachste Form einer Prognose darstellen, im Ergebnis: Wo landet der Jahresumsatz, wenn ab nächstem Monat immer der Planumsatz erreicht werden würde?
Um diese Frage zu beantworten, müssen wir bei dem gegebenen Datenmodell nur eine kleine Anpassung auf dem MDX-Skript des OLAP-Würfels vornehmen.
--R = Ist is null = Planwert wenn Ist nicht vorhanden
SCOPE(
([Wertarten].[Wertarten].[Wertart].&[R],[Measures].[Umsatz]),
[Periode].[Periode].[Monat].MEMBERS
);
THIS =
IIF(
ISEmpty(([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[I])) = TRUE
,([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[P])
,([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[I])
);
END SCOPE;Abb. 2: MDX-Skript HR1
Wie man hier gut erkennen kann, ist nicht einmal eine „echte“ Berechnung notwendig, da Planwerte für jeden Monat vorhanden sind.
Schauen wir uns das Ergebnis direkt in DeltaMaster an:
Abb. 3: Hochrechnung HR1
Soweit, so gut. Allerdings werden Sie sich jetzt wahrscheinlich auch Frage stellen, wie realistisch es ist, dass die aktuellen Umsätze scheinbar nur für komplett abgeschlossene Monate importiert werden? Oder soll wirklich ein Planwert in der Vergangenheit angezeigt werden, wenn dort aus welchen Gründen auch immer keine Istwerte importiert wurden? Wenig realistisch ist die Antwort.
Um die Problematik der Periodenabgrenzung zu umgehen, können wir aber einfach das MDX erweitern.
--S = Ist bis aktueller Monat -1, sonst Plan
SCOPE(
([Wertarten].[Wertarten].[Wertart].&[S],[Measures].[Umsatz]),
[Periode].[Periode].[Monat].MEMBERS
);
THIS =
IIF(
--Rang des aktuellen Periodenelements innerhalb aller Monate des akt. Jahres
RANK(
TAIL(
DESCENDANTS([Periode].[Periode]. CurrentMember
,[Periode].[Periode].[Monat]
)
).ITEM(0), [Periode].[Periode].[Monat].MEMBERS
)
--Prüfung, ob der Monat vor dem akt. Monat liegt, dann Ist-Wert, sonst Plan
<
--Rang des aktuellen Monats innerhalb aller Monate des aktuellen Jahres
RANK(
TAIL(
DESCENDANTS(
strtomem-ber("[Periode].[Periode].[Monat].&["+FORMAT(now(),"yyyyMM")+"]")
,[Periode].[Periode].[Monat]
)
).ITEM(0), [Periode].[Periode].[Monat].MEMBERS
)
-- dann nehme IST-Wert
,([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[I])
,([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[P])
);
END SCOPE;Abb. 4: Hochrechnung HR2
An dieser Stelle bedarf das MDX vermutlich etwas Erklärung. Mit der Funktion RANK() in Kombination mit TAIL() wird die Position des aktuellen kalendarischen Monats innerhalb der beiden Zeitreihen ermittelt und miteinander verglichen. Ist der Rang kleiner, ist es also ein Monat in der Vergangenheit. Damit kann das Problem der Abgrenzung auch dann behoben werden, wenn für den aktuellen Monat bereits Daten im System vorhanden sind.
Widmen wir uns jetzt der weiteren Verfeinerung der Berechnung und damit der Beantwortung anderer Fragestellungen mit Hilfe der Prognose. Wie sieht das Jahresergebnis aus, wenn für das restliche Jahr ein kalkulatorischer Faktor auf das letztjährige Ergebnis aufgeschlagen wird? Und dieser Faktor beispielsweise je Stoffgruppe unterschiedlich sein kann? Zur Veranschaulichung dient hier ein statisch gesetzter Wert für den Faktor, in echten Projekten empfehlen wir die Verlagerung des Faktors in das relationale Datenmodell. Ein Beispiel aus der Praxis: Kosten sollen mit 110%, Erträge aber nur mit 90% berücksichtigt werden (kaufmännische Vorsicht).
--T = Ist bis aktueller Monat -1 sonst Istwert der Vorjahresperiode * Faktor je Stoffgrup-pe
SCOPE(
([Wertarten].[Wertarten].[Wertart].&[T],[Measures].[Umsatz]),
[Stoffgruppen].[Stoffgruppen].[Stoffgruppe].MEMBERS,
[Periode].[Periode].[Monat].MEMBERS
);
THIS =
IIF(
--Rang des aktuellen Periodenelements innerhalb aller Monate des aktuellen Jahres
RANK(
[Periode].[Periode].CurrentMember
, [Periode].[Periode].[Monat].MEMBERS
)
--Prüfung, ob der einzelne Monat vor dem aktuellen Monat liegt
<
--Rang des aktuellen Monats innerhalb aller Monate des aktuellen Jahres
RANK(
strtomember("[Periode].[Periode].[Monat].&["+FORMAT(now(),"yyyyMM")+"]")
, [Periode].[Periode].[Monat].MEMBERS
)
,([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[I])
,CASE
WHEN [Stoffgruppen].[Stoffgruppen].CurrentMember.PROPERTIES("Br2") = 'Werkstoff 1'
THEN ([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[I]
,ParallelPeriod([Periode].[Periode].[Monat],12,[Periode].[Periode].CurrentMember))
WHEN [Stoffgruppen].[Stoffgruppen].CurrentMember.PROPERTIES("Br2") = 'Werkstoff 2'
THEN ([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[I]
,ParallelPeriod([Periode].[Periode].[Monat],12,[Periode].[Periode].CurrentMember))
* 1.1
ELSE ([Measures].[Umsatz], [Wertarten].[Wertarten].[Wertart].&[I]
,ParallelPeriod([Periode].[Periode].[Monat],12,[Periode].[Periode].CurrentMember))
* 0.9
END
);
END SCOPE;Abb. 5: Hochrechnung HR3
Im CASE-Statement wird jetzt bei einem bestimmten Wert einer Elementeigenschaft für die Berechnung der Vorjahres Ist-Wert * dem kalkulatorischen Faktor herangezogen. Wir haben in diesem Beispiel die Elementeigenschaft „Br2“ nur exemplarisch verwendet, da diese Beispieldatenbank keine Kontodimension für die Trennung nach Kosten und Erträgen beinhaltet.
Grundsätzlich sollten CASE()-Anweisungen vermieden werden, da derartige Berechnungen mit steigendem Datenvolumen und Komplexität des Datenmodells langsam sind bzw. werden. Der deutlich elegantere Weg wäre auch hier die Verwendung einer Attributhierarchie über die verwendete Elementeigenschaft. Die Idee und Umsetzung mit MDX sollten aber auch aus der folgenden Variante HR4 hervorgehen.
In DeltaMaster stellen wir die beiden neuen Prognosen zusätzlich dar. Wie man gut erkennen kann, ergeben sich mitunter völlig unterschiedliche Ergebnisse für das zu erwartende Jahresergebnis. In den ersten beiden dargestellten Wertarten HR1 und HR2 müssen die gleichen Werte stehen, da nur die Logik zur Ermittlung des Zeitpunktes, ab welchem Monat der Planwert zu verwenden ist, geändert wurde.
Abb. 7: Hochrechnung HR1 - HR3
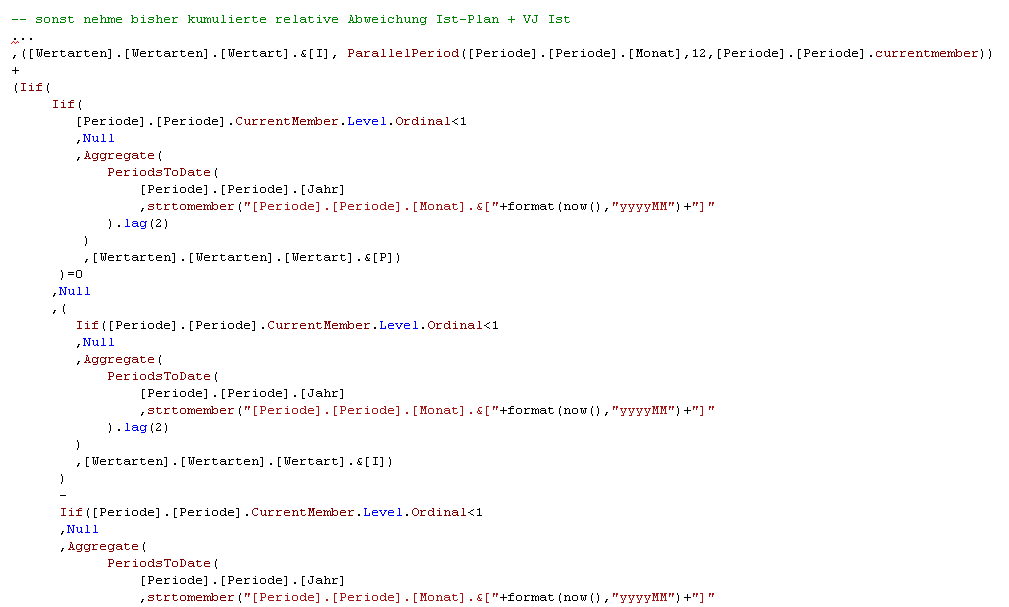
Mit diesem Ergebnis waren wir bis dato zufrieden. In einem Kundenprojekt wurden wir dann aber mit der Fragestellung konfrontiert, wie denn das Jahresergebnis aussieht, wenn sich Stand heute die tatsächliche Abweichung zwischen Ist und Plan ohne Eingriff von Seiten der Unternehmenssteuerung über die kommenden Monate weiterverteilt? Im Gespräch stellte sich heraus, dass der Kunde damit nicht einen fest definierten Faktor für die Hochrechnung meinte, sondern es sollte doch mit der bisher aufgelaufenen (kumulierten), relativen Ist-Plan-Abweichung prognostiziert werden. Da zu dem Zeitpunkt jegliche Kumulation in dem Kundenprojekt in DeltaMaster gerechnet wurde, musste also die Berechnung irgendwie auf das MDX-Skript des Würfels verlagert werden. Die erste Lösung war, mit Hilfe des MDX.log die Berechnung tatsächlich nachzubauen. Hier ein Auszug des MDX, welches dafür notwendig ist, die Betonung liegt auf „Auszug“:
-- sonst nehme bisher kumulierte relative Abweichung Ist-Plan + VJ Ist
...
,([Wertarten].[Wertarten].[Wertart].&[I], ParallelPeriod([Periode].[Periode].[Monat],12
,[Periode].[Periode].Currentmember))
+
(Iif(
Iif([Periode].[Periode].CurrentMember.Level.Ordinal<1
,Null
,Aggregate(
PeriodsToDate(
[Periode].[Periode].[Jahr]
,strtomember("[Periode].[Periode].[Monat].&["+format(now(),"yyyyMM")+"]"
).lag(2)
)
,[Wertarten].[Wertarten].[Wertart].&[P])
)=0
,Null
,(
Iif([Periode].[Periode].CurrentMember.Level.Ordinal<1
,Null
,Aggregate(
PeriodsToDate(
[Periode].[Periode].[Jahr]
,strtomember(
"[Periode].[Periode].[Monat].&["+format(now(),"yyyyMM")+"]"
).lag(2)
)
,[Wertarten].[Wertarten].[Wertart].&[I])
)
...Abb. 8: Auszug Berechnung relative, kumulierte Abweichung
Das Ergebnis funktioniert, man erkennt aber schon, dass es lang ist und unübersichtlich wird. Viel schlimmer, es ist aufgrund der verwendeten Funktionen Iif() und StrToMember() auf größeren Datenmodellen sicherlich nicht performant.
Jetzt geht es an die Optimierung. Dazu sind ein paar kleine Modellerweiterungen notwendig.
- Die Kumulation wird auf das MDX-Skript des Würfels verlagert
- Implementierung einer Analysewertgruppe, um die Vergangenheit und die Zukunft (Monate) zu kennzeichnen
- Erstellung einer Attribut-Hierarchie in der Dimension Periode, um den Datenraum des Scopings so klein wie möglich zu halten
- Berechnung per MDX im Skript des Würfels in 2 Teilschritten
Das Kumulationselement definieren wir wie folgt auf dem Würfel:
CREATE MEMBER CURRENTCUBE.[Kumulation].[Kumulation].KUM_SKRIPT
AS
AGGREGATE(
PeriodsToDate([Periode].[Periode].[Jahr],[Periode].[Periode].CurrentMember)
,[Kumulation].[Kumulation].[Kumulation].&[1]
)
,VISIBLE = 1Abb. 9: Kumulation auf OLAP-DB
Eine kurze Erklärung der folgenden Darstellungen: Die Kennzahl HR_Flag_Future kennzeichnet alle Monate in der Zukunft, ausgehend vom heutigen Monat, mit einer 1. Die Kennzahl HR_Flag_History markiert die Vergangenheit mit einer 1.
Abb. 10: Markierung der Monate
Die relationalen Modellerweiterungen bzgl. der Attributhierarchie implementieren wir mit Hilfe von DeltaMaster Modeler in das multidimensionale Modell und lassen den Würfel anschließend neu erstellen. Nun sind wir in der Lage, die MDX-Berechnung in Angriff zu nehmen.