Den letzten Blogbeitrag zum Thema Geoberechnungen setzen wir nun mit einer genauen Betrachtung realer Zusammenhänge und Abstände auf unseren Landkarten in Bezug auf 5-stellige PLZ-Gebiete fort. Unterschiedliche Lösungen (Mappings) sind möglich und die aktuellen Kartendaten mit jeweils Längen- und Breitengradangabe sind u.a. über unseren Lieferanten zu beziehen. Zuerst ein wenig Hintergrundwissen zur Auffrischung.
Geoberechnung allgemein (Hintergrund)
Aristoteles begründete im 4. Jahrhundert mit drei Thesen seine Vermutung für eine Kugelgestalt: 1. wegfahrende Schiffe verdecken den Rumpf am Horizont, 2. in südlichen Ländern erscheinen südliche Sternbilder höher über dem Horizont, und 3. der Erdschatten ist bei einer Mondfinsternis rund. Mit dieser Tatsache beginnen unsere Berechnungsprobleme.
Die exakte Berechnung des Abstandes zweier Punkte auf einer Kugel erfolgt mittels des Seitenkosinussatzes (sphärische Trigonometrie), sie ist jedoch durch einen erhöhten Rechenaufwand gekennzeichnet, der die Vorteile einer Berechnung im Frontend nivelliert. Gegeben sind hierbei die Längen-/Breitengradpaare des Start- und Zielpunktes; die Berechnung ist in DeltaMaster als Analysewert realisiert.
Eine kleine Anmerkung sei erlaubt: Aufgrund der Polabplattung kommt eigentlich erschwerend hinzu, dass die Annahme einer Kugelform für die Erde für größere Entfernungen nicht hinreichend genau ist, und man anstatt dessen einen/oder sogar mehrere Rotationsellipsoid(e) berücksichtigt; der WGS84-Ellipsoid (World Geodetic System 1984, hierbei beträgt die Differenz der Halbachsen ca. 21 km) ist Grundlage der GPS-Navigation (NAVSTAR-Satelliten).
Analysewert: Abstand_exakt
#1 Ziel_Breitengrad
#2 Ziel_Laengengrad
#3 Standort_Breitengrad
#4 Standort_Laengengrad
-- exakte Entfernungsberechnung mit dem Seitenkosinussatz
-- distance = acos(
-- sin(lat1) * sin(lat2) +
-- cos(lat1) * cos(lat2) * cos(lon2 - lon1)
-- ) * r
-- r = 6378.388 (Erdradius in km), 180/PI = 57.2957795130823
ACOS(
SIN( #3 / 57.2957795130823 ) * SIN(#1 / 57.2957795130823 ) +
COS( #3 / 57.2957795130823 ) * COS(#1 / 57.2957795130823 ) *
COS( (#2 - #4) / 57.2957795130823 )
) * 6378.388
Eine Alternative wäre z. B. die exakte Vorberechnung aller Abstände von und zu allen Postleitzahlen, also der CROSSJOIN der Tabelle PLZ5 (ca. 8.200 Einträge) mit sich selbst. Dies führt zu knapp 35 Mio. Einträgen (bei einer halbseitig besetzten Matrix) und knapp 1.5 GB Speicherbedarf. Dies ist wenig praktikabel.
Für unsere Zwecke reicht meist jedoch eine einfachere Berechnungsvorschrift, die auf einem karthesischen Modell fußt. Der Abstand zweier ganzzahliger Breitengrade beträgt im Mittel 111,32 km, ist aber wegen der Erdabplattung auf den Polkappen nicht konstant. Der durchschnittliche Abstand zwischen zwei Längenkreisen ist jedoch nicht konstant, lässt sich aber aus einer Betrachtung des über alle PLZ-Abstände summierten Fehlers im Vergleich zu einer exakten Betrachtung optimieren. Somit haben wir eine angepasste Variante mit optimierten Berechnungsparametern, die den Berechnungsfehler minimiert und die schnelle Berechnung im DeltaMaster-Frontend ermöglicht.
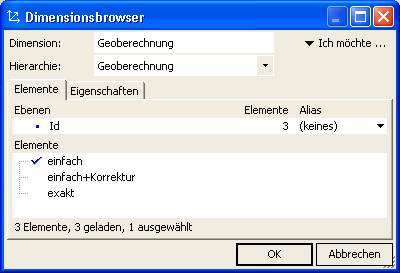
Um uns einen Vergleich verschiedener “Berechnungsmöglichkeiten” zu erlauben, kann es sinnvoll sein, alle Vorschriften in einem Analysewert zu vereinen und die Auswahlvorschrift durch eine eigene Dimension/Measuregroup zu steuern.
Nachfolgend finden Sie die Abstandsformel mit einer Parametrierung über diese Kennzahlendimension.
Analysewert: Abstand
#1 Ziel_Breitengrad
#2 Ziel_Laengengrad
#3 Standort_Breitengrad
#4 Standort_Laengengrad
#5 Geoberechnung
-- variable Abstandsberechnung
CASE #5
WHEN 1 THEN
SQR( … ) /* einfache Abstandsberechnung */
WHEN 2 THEN
SQR( COS ( … ) … ) /* einfache + Kosinussatz Abstandsberechnung */
WHEN 3 THEN
ACOS( … ) /* exakte Abstandsberechnung auf Kugeloberfläche */
ELSE NULL
END
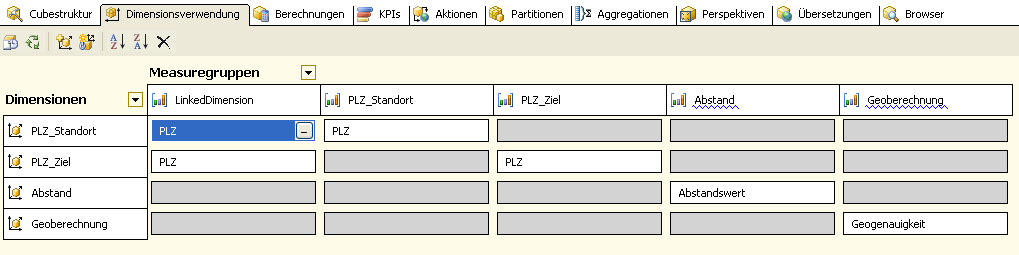
Die Modellierung muss entsprechend unserer Aufgabenstellung adaptiert werden; es sollen schließlich zwei Dimensionen mit PLZ verbunden sein und in einer Kreuztabelle verknüpft dargestellt werden können. Die Dimensionsverwendung aus den Analysis Services ist wie folgt.
Ausgehend von der reinen Abstandsberechnung lassen sich weitere Analysewerte definieren, die die Modellierung von Geoberechnungen ermöglichen. Dazu zählt beispielsweise die Bestimmung einer Abstandsregion:
Analysewert: Abstand_Region
#1 Abstand #2 Abstand_min #3 Abstand_max -- Region: Abstand_min <= x < Abstand max IIF( #1 >= #2 AND #1 < #3, #1, NULL )
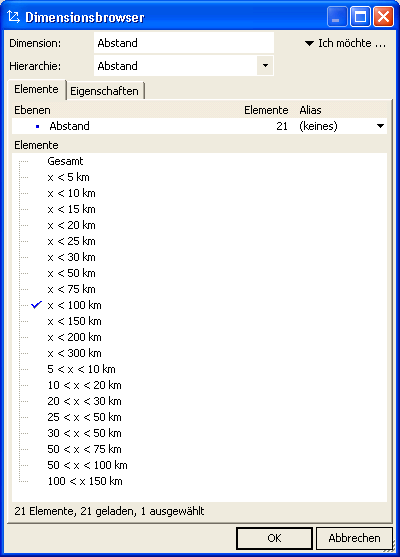
Diese wird parametriert über eine Abstandsdimension:
Die Parametrierung ist auch über weiterführende Analysewerte möglich, wie z. B. dBOOL, der den Wert 1 (die Ziel-PLZ ist innerhalb der eingestellten Abstandsregion) oder NULL annehmen kann. Damit lassen sich in der Datenbank vorhandene Analysewerte (z. B. Umsatz, Deckungsbeitrag etc.) in einen Geobezug überführen.
Analysewert: dBOOL
#1 Abstand_Region
[PLZ_Standort] Dimension ID:6
-- liefert den Wert 1, wenn Ziel-PLZ in einem Abstandsbereich zu
-- mindestens einer Standort-PLZ
IIF(
COUNT( ({<view6>}, #1), EXCLUDEEMPTY ) >0,
1,
NULL
)
Weitere Analysewerte lassen sich äquivalent wie folgt erstellen:
Analysewert Erklärung
dBOOL Liefert den Wert 1, wenn die Ziel-PLZ in einem Abstandsbereich zu mindestens einer Standort-PLZ.
dCNT Liefert die Anzahl der Überdeckungen, d.h. wie viele Standort-PLZ sich in einem Abstandsbereich zu der Ziel-PLZ befinden.
dMIN Ergibt den minimalen Abstand einer Ziel-PLZ zu allen Standort-PLZ unter Berücksichtigung der Regionsbeschränkung.
dMAX Ergibt den maximalen Abstand einer Ziel-PLZ zu allen Standort-PLZ unter Berücksichtigung der Regionsbeschränkung.
dOVL Liefert den Wert 1, wenn mindestens eine Überlappung einer Standort-PLZ zu einer Ziel-PLZ vorhanden ist unter Berücksichtigung der Regionsbeschränkung.
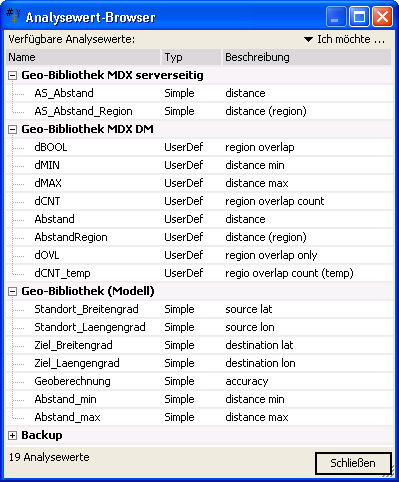
Die erstellte Analysewert-Bibliothek im Überblick:
Beispiel: PLZ-Zuordnung
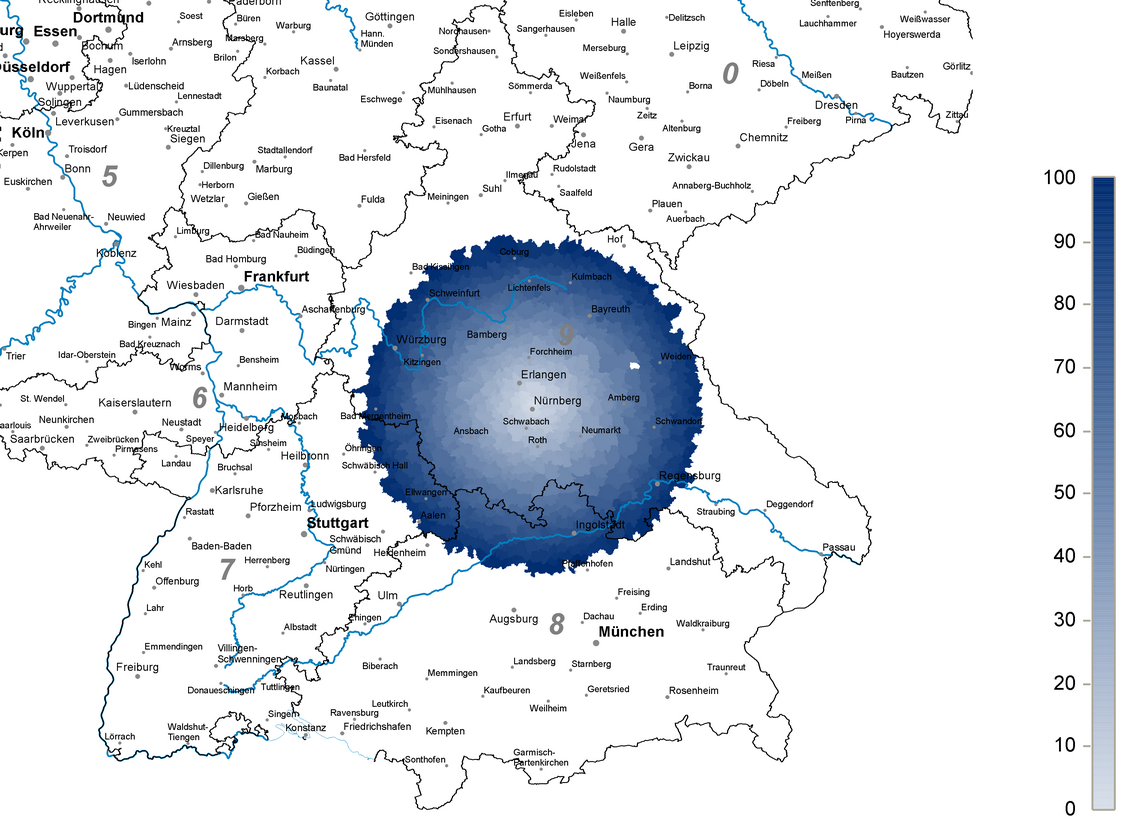
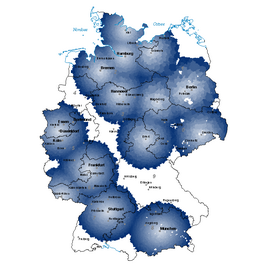
Anhand einiger einfacher Beispiele sollen die Möglichkeiten aufgezeigt werden. Legen wir beispielsweise die Standort-PLZ auf 90409 (Stammsitz Bissantz & Company) fest und legen in der Abstandsdimension den Umkreis x<100km fest, können wir das Ergebnis in der DeltaMaster Geo-Analyse darstellen.
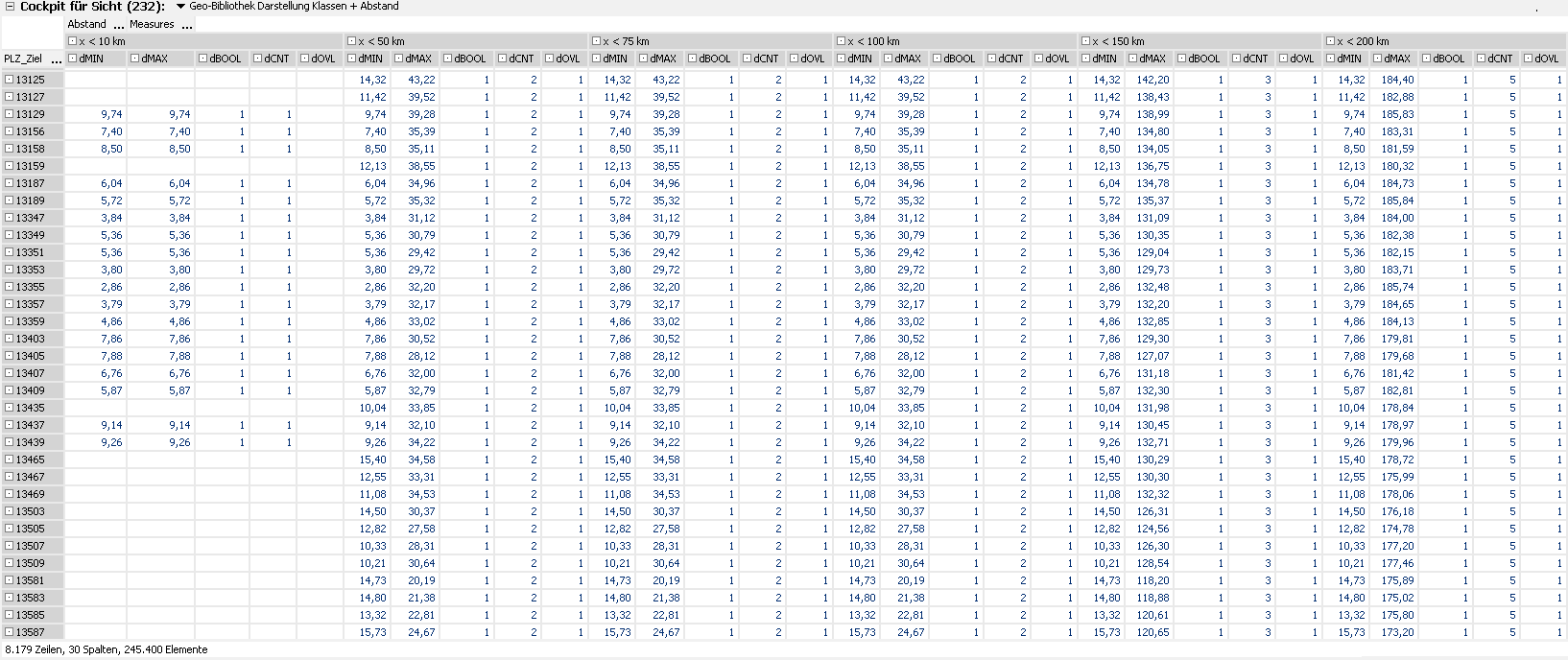
Für ein umfangreicheres Beispiel tragen wir im Sichtkontext die 16 PLZ der Landeshauptstädte ein
und zeigen in einer Tabelle die Mächtigkeit der Analysewerte. In der Pivottabelle sind die 5 Analysewerte in 6 Abstandsregionen auf 8.179 PLZ-Werte aufgetragen, es ergeben sich insgesamt 245.000 Einzelwerte bzw. Berechnungen.
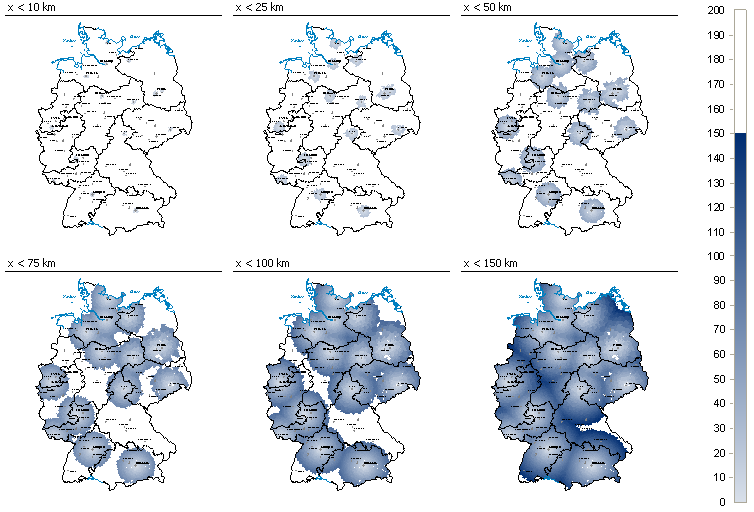
Einen Ausschnitt der Pivottabelle (x<100km) wollen wir mittels der DeltaMaster Geo-Analyse darstellen. Die dargestellten Analysewerte zeigen deren Mächtigkeit auf.
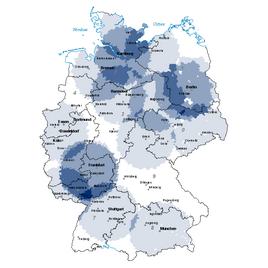
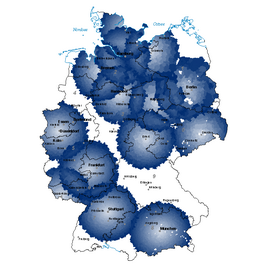
dBOOL (Zielgebiet) / dCNT (Anzahl Überlappe)
dMIN (minimaler Abstand), dMAX (maximaler Abstand)
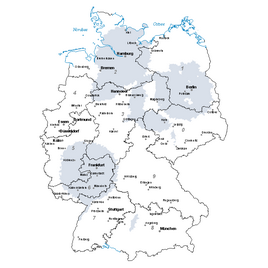
dOVL (reine Überlappgebiete)
Die vorgestellten Geo-Analysen lassen sich als Analysevorlagen ablegen, um beispielsweise Small Multiples über Regionen iteriert darzustellen.
Bei der Umsetzung Ihrer Ideen ist Ihnen unser Bissantz-Consulting-Team gerne behilflich.
Im letzten Blogbeitrag werden wir uns mit Geokoordinaten auf Adressebene (Straße, Ort), mit deren Generierung sowie mit einer einfachen Konkurrenzanalyse beschäftigen.