Berechnungen lassen sich in DeltaMaster an vielen Stellen einfügen. Eine möglichst abstrakte Definition der Berechnung erhöht ihre Wiederverwendbarkeit.
Dies wird im folgenden Blogbeitrag für die Berechnung von Anteilswerten gezeigt. Als Beispiel dient eine Fragestellung aus einem DeltaMaster-Präsentationsworkshop:
Bestehen regionale Unterschiede in den Umsatzanteilen, die das Produkt X an der übergeordneten Produktgruppe XYZ hat?
Zellbasierte Berechnung
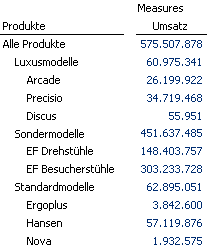
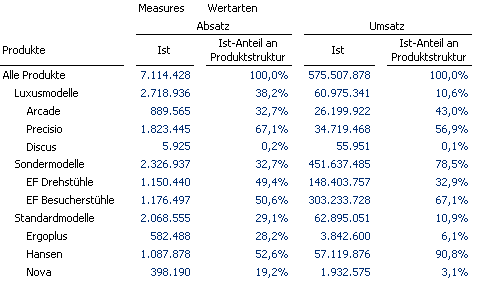
In formelbasierten, zellorientierten Berichten wird ein Anteilswert im einfachsten Fall als Quotient aus anderen Zellwerten in einer Zelle definiert. Ausgehend von unserer folgenden Produktstrukur verdeutlichen wir die Vorgehensweise:
Ein typisches Beispiel für zellbasierte Berechnung ist der Flexreport in DeltaMaster. Diese Art der Berechnung hat jedoch den Nachteil, im Bericht definiert zu sein, und damit auf diesen Bericht beschränkt zu sein. Allgemein ausgedrückt, ist es eine sehr konkrete Lösung für einen ganz konkreten Fall.
Die Kunst der Modellierung für und mit DeltaMaster besteht jedoch darin, abstrakte Modellierungen zu finden, die eine ganze Klasse von Fragestellungen lösen.
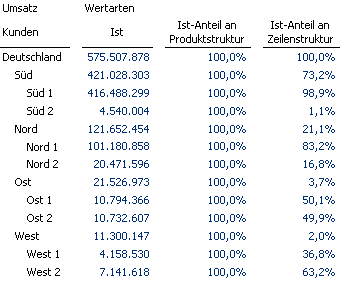
Die obige Fragestellung aus einem DeltaMaster-Präsentationsworkshop verdeutlicht dies. Die regionalen Unterschiede lassen sich sehr gut in einer Geo-Analyse aufzeigen. Doch lässt sich eine Formel aus dem Flexreport nicht in den Analysemodulen verwenden.
Benutzerdefinierter Analysewert
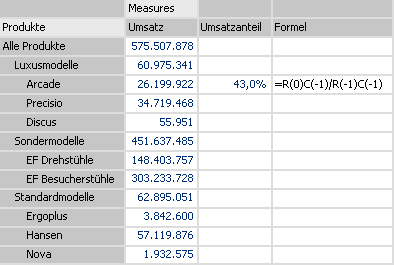
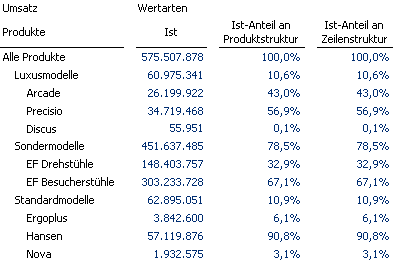
Für die Verwendung in den Analysemodulen definieren wir den Umsatzanteil X im einfachsten Fall als Umsatz des Produktes X geteilt durch den Umsatz der Produktgruppe XY.
Der MDX Ausdruck für einen benutzerdefinierten Analysewert, sofern die Berechnung nicht über den Quotienten zweier Filterwerte definiert wird, sieht ganz einfach aus:
( [Produkte].[Produkte].[Produkt].&[X], [Measures].[Umsatz] ) / ( [Produkte].[Produkte].[Produktgruppe].&[XY], [Measures].[Umsatz] )
Das Problem scheint gelöst, doch schon die nächste Frage zwingt uns zur Überarbeitung der Definition:
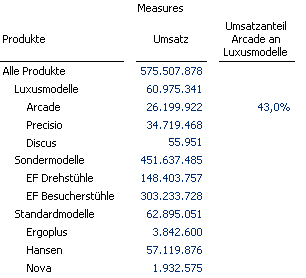
Wie sieht es denn beim Produkt B in der Produktgruppe BCD aus?
Ist jetzt eine weitere Kennzahl zu definieren? Die Lösung liegt darin, den bereits angelegten Analysewert so zu definieren, dass er dynamisch wirkt:
( [Produkte].[Produkte].CurrentMember, [Measures].[Umsatz] ) / ( [Produkte].[Produkte].CurrentMember.Parent, [Measures].[Umsatz] )
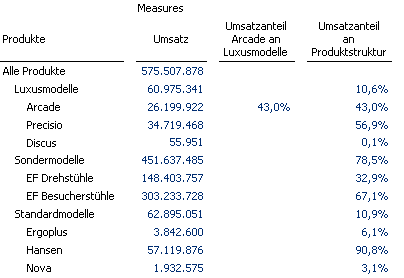
Damit ist jetzt nicht nur der Anteil für alle Produkte, sondern der Anteil an der übergeordneten Produktgruppe sowie gleichzeitig auch der Anteil der Produktgruppen an der übergeordneten Produkthauptgruppe sowie deren Anteil an Gesamt berechnet.
Hierbei kann der Operator Parent auch direkt auf der Hierarchie angewendet werden, da er implizit CurrentMember enthält:
( [Produkte].[Produkte].CurrentMember, [Measures].[Umsatz] )
/
( [Produkte].[Produkte].Parent, [Measures].[Umsatz] )
Um auch für die Elemente auf oberster Ebene eine korrekten Anteil von 100% oder eine leere Zelle anzuzeigen, wird eine Fallunterscheidung mittels Iif-Statement eingebaut:
Iif ( [Produkte].[Produkte].CurrentMember.Level.Ordinal= 0, 1, /* null */
( [Produkte].[Produkte].CurrentMember, [Wertarten].[Wertarten].[Wertart].&[I] )
/
( [Produkte].[Produkte].Parent, [Wertarten].[Wertarten].[Wertart].&[I] )
)
Abstraktion vom Analysewert
Eine weitere Abstraktionsstufe wird nötig, sobald die Frage nach einem anderen Basiswert gestellt wird.
Wie sehen die Anteile bezogen auf die Absatzmenge aus?
Abstrahiert wird hier der konkrete Basiswert. Bei der Entscheidung, wo diese analysewertunabhängige Berechnung zu definieren ist, hilft folgender Grundsatz mehrdimensionaler Berechnungen weiter:
Abstrakte Berechnungen lassen sich nie in der Dimension definieren, die das zu abstrahierende Element enthält.
Die Analysewerte im OLAP Modell sind dabei wie eine Dimension zu betrachten.
Ein Kandidat für die Berechnung ist die Dimension Wertart. Ein in der Dimension Wertart angelegtes berechnetes Element Ist-Anteil an Produktstruktur lässt sich wie folgt definieren.
( [Produkte].[Produkte].[CurrentMember], [Wertart].[Ist] ) / ( [Produkte].[Produkte].CurrentMember.Parent, [Wertart].[Ist] )
Der aufmerksame Leser wird jetzt schon aus der Formel erkennen, dass die Nennung eines konkreten Elements der Dimension Wertart (Ist), Spielraum für weitere Abstraktionen lässt.
Die Verlagerung auf eine andere Dimension wie z.B. die Periodenansicht, lässt dann eine Abstraktion von Wertarten zu, konkretisiert dann aber genau ein Periodenansichtselement.
Abstraktion von der Berechnungsdimension
Eine weitere Abstraktion von allen Dimensionen im Modell lässt sich nur erreichen, indem man das Modell selbst in die Überlegungen mit einbezieht:
Eine weitere Hilfsdimension Berechnungen ließe also eine weitere Abstraktion zu.
Hier sind wir jetzt jedoch bei theoretischen Überlegungen angekommen, da für die Berechnung der im Beispiel aufgeführten Anteilswerte in der Praxis keine Modellerweiterung vorgenommen werden soll.
Wichtig ist jedoch, dass man diese Abstraktionsmöglichkeit bei der Konzeption von (vor allem komplexeren) Modellen einbezieht.
Abstraktion der Strukturdimension
Ein zweiter Ansatz zur weiteren Abstraktion der Anteilsberechnung liegt in der Dimension selbst. Mit MDX ist es möglich, die Zeilendimension erst bei der Ausführung der Abfrage zu definieren:
( Axis(1).Item(0).Dimension.CurrentMember, [Wertarten].[Wertarten].[Wertart].&[I] ) / ( Axis(1).Item(0).Dimension.Parent, [Wertarten].[Wertarten].[Wertart].&[I] )
Die Anteilsberechnung ist also immer noch korrekt, auch wenn die Zeilendimension im Bericht ausgetauscht wird.
Jedoch setzt man hierbei eine wohl definierte Abfragestruktur voraus, die durch Benutzerinteraktion nicht immer erhalten bleibt. So genügt ein einfaches Transponieren der Pivottabelle, um die Abfragestruktur zu verändern. Weiterhin wird durch die Analysekettentechnik das definierte Element in Abfragen eingebunden, deren Struktur bei der Definition der Berechnung nicht berücksichtigt werden kann.
So reizvoll diese letzte Abstraktionsstufe auch ist, vor dem praktischen Einsatz ist dringend abzuraten.