Bei der momentan herrschenden Hitze gibt es nur ein Thema – das Wetter! Wie verhalten sich etwa die Temperaturen der letzten Monate? Wie setzt man DeltaMaster ein, um die Trends von Zeitreihendaten leichter erfassen zu können?
Wetterdaten werden gerne genutzt, um beispielsweise Prognosen in zumeist temperatur- und regenabhängigen Sektoren zu verbessern. Dazu gehören etwa die Landwirtschaft und der Tourismus, aber auch die Gesundheit des Menschen wird vom Wetter beeinflusst.
Bevor man anfängt, komplexe Modelle zu postulieren, möchte man sich erstmal einen Überblick verschaffen.
Nehmen wir die beispielsweise die Temperaturen (Quelle am Seitenende!) aus den letzten 500 Tagen (12.3.2017 – 24.7.2018) in Nürnberg her. Es handelt sich hier beim Tageswert um einen Mittelwert aus 24 stündlich in zwei Meter Höhe gemessenen Temperaturen (bitte klicken Sie auf die Grafik für eine vergrößerte Darstellung!):
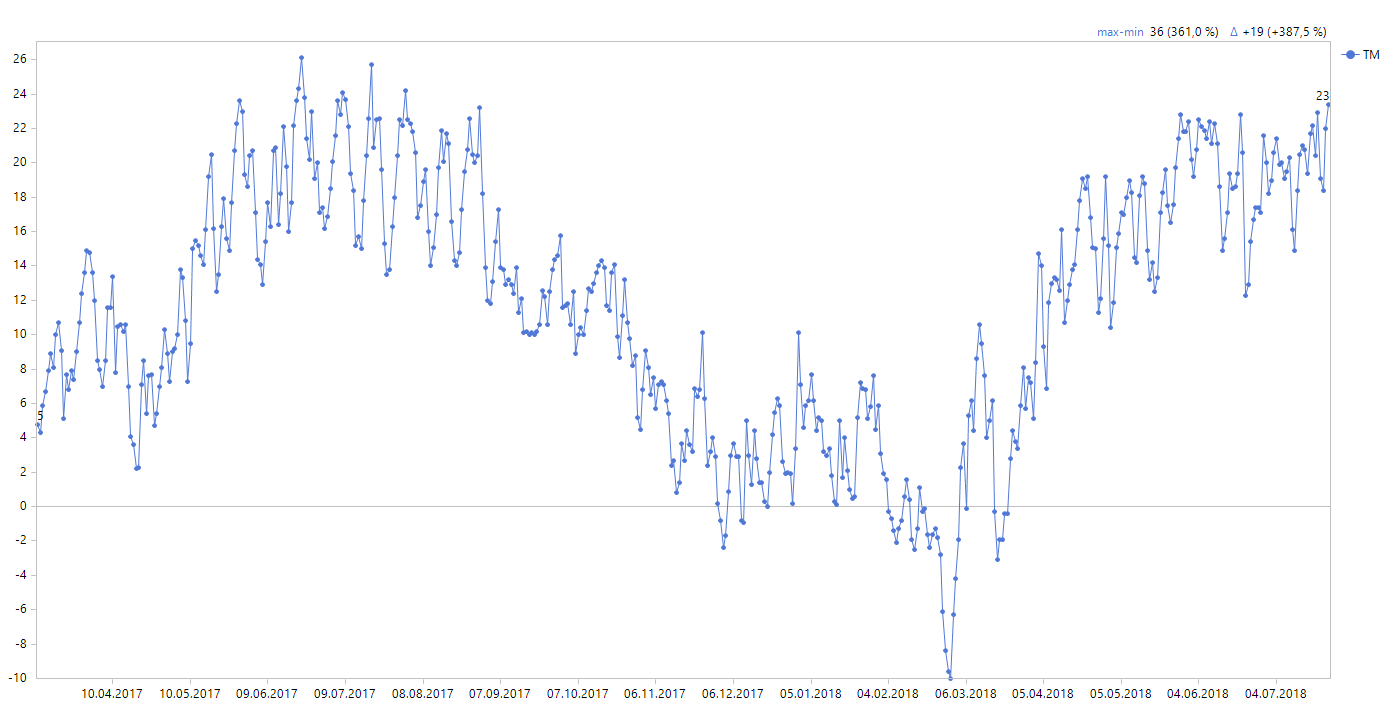
Temperaturen in Nürnberg vom 12.3.2017 bis zum 24.7.2018
Die Temperatur schwankt bzw. “zappelt” geradezu um einen bis dato noch nicht sichtbaren Trend und genau diesen möchten wir nun darstellen.
Dazu legen wir unter Modellieren/Logik in der Periodenansicht (Time Utility) ein Zeitanalyseelement “Gleitende Aggregationen” an – hier mit einem roten Rahmen versehen:
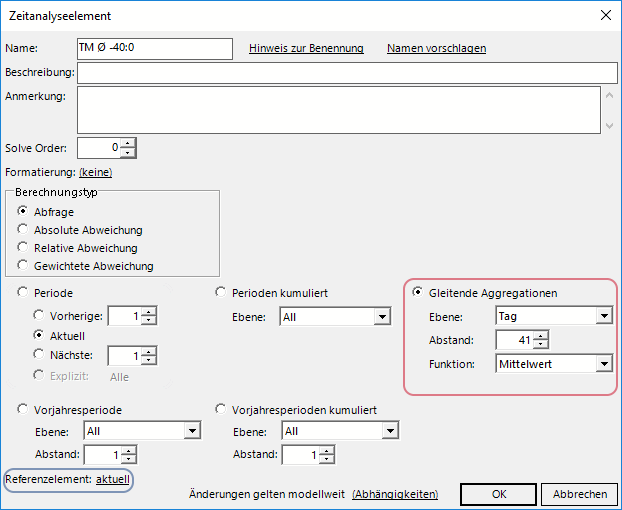
Zeitanalyseelement “Gleitende Aggregationen”
Was bewirkt dieses Element? Es werden die letzten 41 Tageswerte – inklusive des aktuellen Tages – hergenommen und der Mittelwert berechnet. Wir verwenden hier die zusätzliche Bezeichnung (-40:0),
um auszudrücken, dass unser relevantes Fenster 40 Tage vor dem aktuellen Tag beginnt und mit dem aktuellen Tag endet.
Unten links ist eingerahmt ein Referenzelement zu sehen, das standardmäßig auf aktuell eingestellt ist.
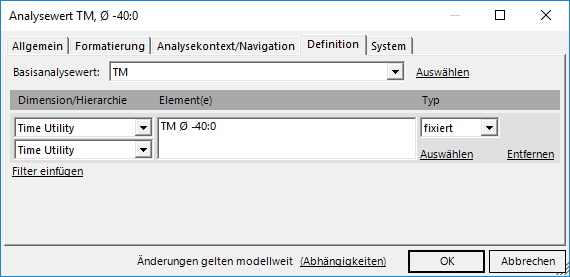
Um die geglättete Zeitreihe gleichzeitig mit der Originalreihe sehen zu können, muss ein Filterwert angelegt werden, d. h. in diesem wird immer der gleitende Durchschnitt aus dem Zeitanalyseelement verwendet, auch wenn die Sicht auf aktuell eingestellt ist:
Eine neue Zeitreihenanalyse wird angelegt und die Temperatur (TM) und der Filterwert werden per Drag-and-drop in das Diagramm gezogen:
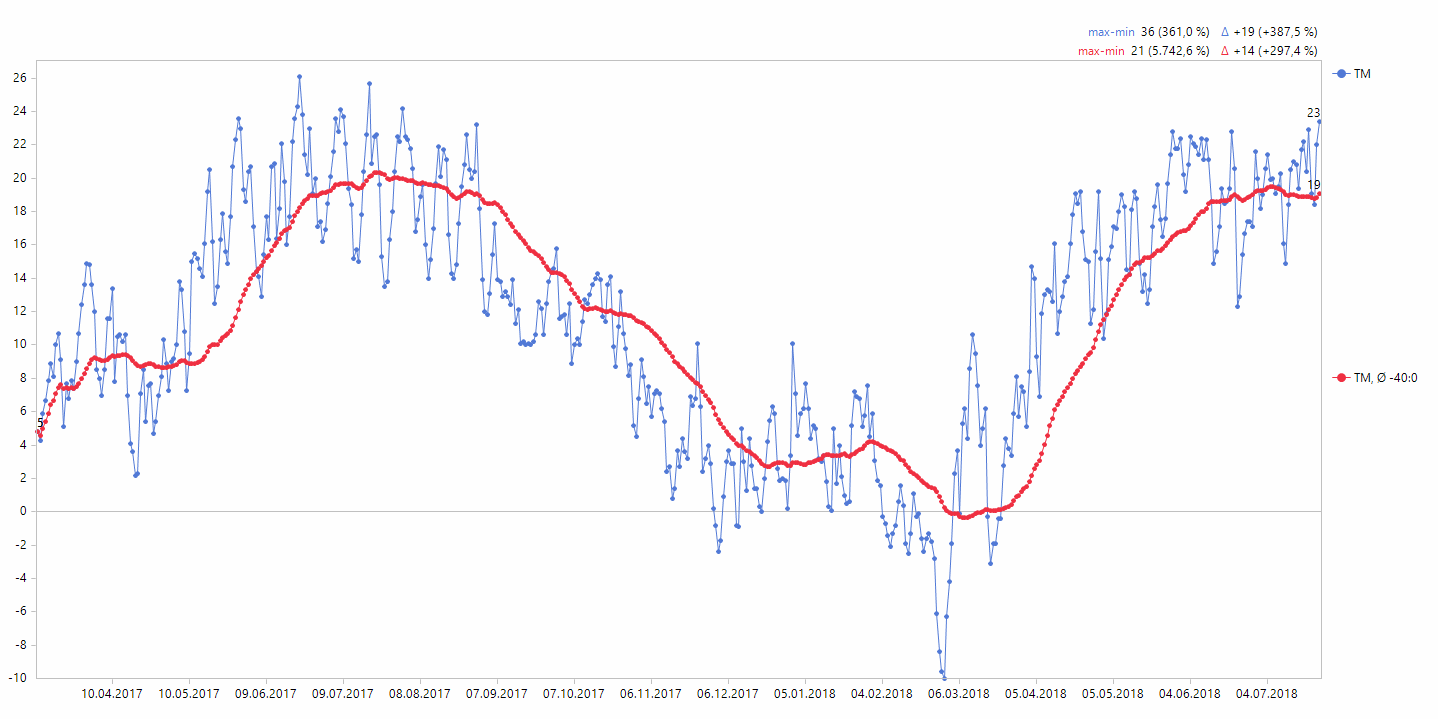
Temperaturmittel (TM) und einfacher gleitender Durchschnitt
Dies ist schon ein Schritt in die richtige Richtung, aber es gibt etwas Störendes an dieser Darstellung. Da der Mittelwert aus den letzten 41 Werten berechnet wird, hängt der Durchschnitt der aktuellen Entwicklung immer hinterher: Wenn die Temperatur bereits wieder steigt wie von März bis Juni 2018, ist der Mittelwert immer zu niedrig angesetzt und liegt deutlich unterhalb der Zeitreihe. Analoges gibt es für fallende Sequenzen zu berichten – hier liegt der Mittelwert immer zu hoch.
Es wäre wünschenswert, wenn der Mittelwert zentriert um einen Tag berechnet wird. Bei 41 Tagen wäre der gewünschte Zeitraum 20 Tage vor dem heutigen Tag bis 20 Tage nach dem heutigen Tag.
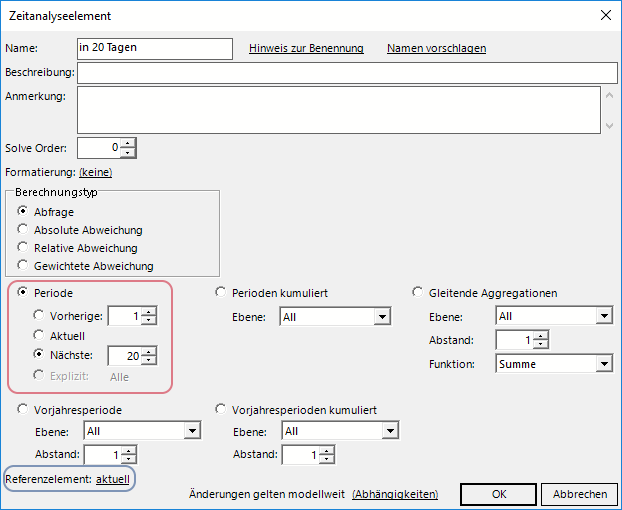
Um eine solche Berechnung darstellen zu können, benötigen wir ein weiteres Zeitanalyseelement, welches wir hier “In 20 Tagen” nennen. Hiermit kann zum aktuell eingestellten Tag der Wert in 20 Tagen ermittelt werden:
Wäre ein Datum auf Monatsebene eingestellt, erhielte man den Wert in 20 Monaten, aber in unserem Beispiel bleiben wir die gesamte Zeit auf Tagesebene.
Nun kommt der Trick: Wenn man beim Zeitanalyseelement für die Glättung als Referenzelement “In 20 Tagen” verwendet, werden die 40 Tagen rückwärts von diesem Wert aus gerechnet und man landet dann bei einem Fenster (-20:+20). Zur Vollständigkeit hier noch einmal die Darstellung des neuen Zeitanalyseelements:
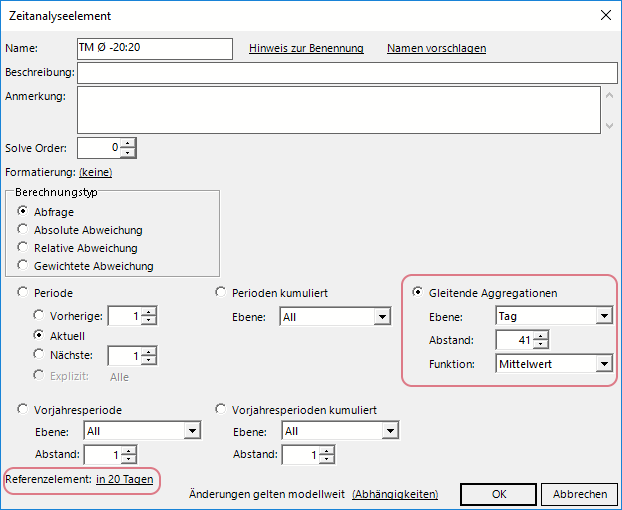
Zentrierter Durchschnitt mit Referenzelement in 20 Tagen
Wird wieder ein Filterwert mit diesem Zeitanalyseelement gebildet und in einer neuen Zeitreihenanalyse mit dem Originalwert angezeigt, so sieht das nun deutlich besser aus:
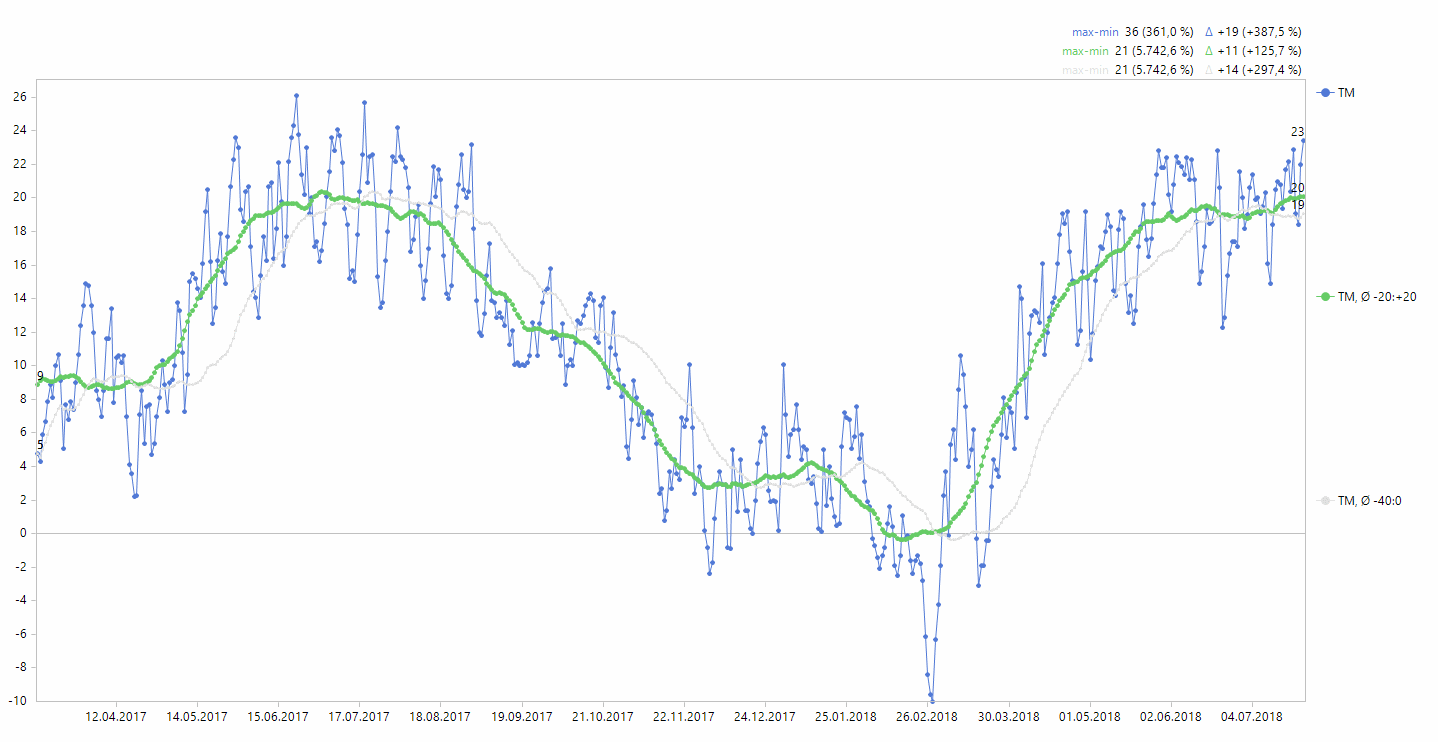
Temperaturmittel (TM) und zentrierter Durchschnitt
Die geglättete Kurve läuft nun schön durch die Messpunkte und gibt den Verlauf besser wieder als unser erster Versuch, der hier nur noch in dünnem Grau zu sehen ist. Damit die Werte am linken Rand korrekt berechnet werden, muss die Zeitdimension auch die letzten 20 Tage vor dem ersten auftretenden Wert enthalten, auch wenn für diesen Zeitraum möglicherweise keine Temperaturen vorliegen sollten.
Hier war die Länge des Glättungsfensters mit 41 ziemlich willkürlich gewählt; eine ungerade Zahl wurde deshalb genommen, um einen symmetrischen Durchschnitt +/- 20 Tage um den aktuellen Zeitpunkt berechnen zu können.
Häufig ergibt sich die Länge des Fensters aber auch aus aus einem sich wiederholenden Rhythmus.
Im folgenden Beispiel sei der monatliche Umsatz gegeben, der einen typischen Jahresverlauf – beispielsweise durch Wettereigenschaften verursacht – aufweist, gleichzeitig aber erfreulicherweise mit einem stetig wachsenden Trend glänzt.
Sei zunächst aus didaktischen Gründen der einfache, nicht zentrierte Durchschnitt aus den letzten 12 Monaten genommen. Steht man etwa auf März 2017, wird hier der Durchschnitt aus den Monaten April 2016 bis März 2017 berechnet:
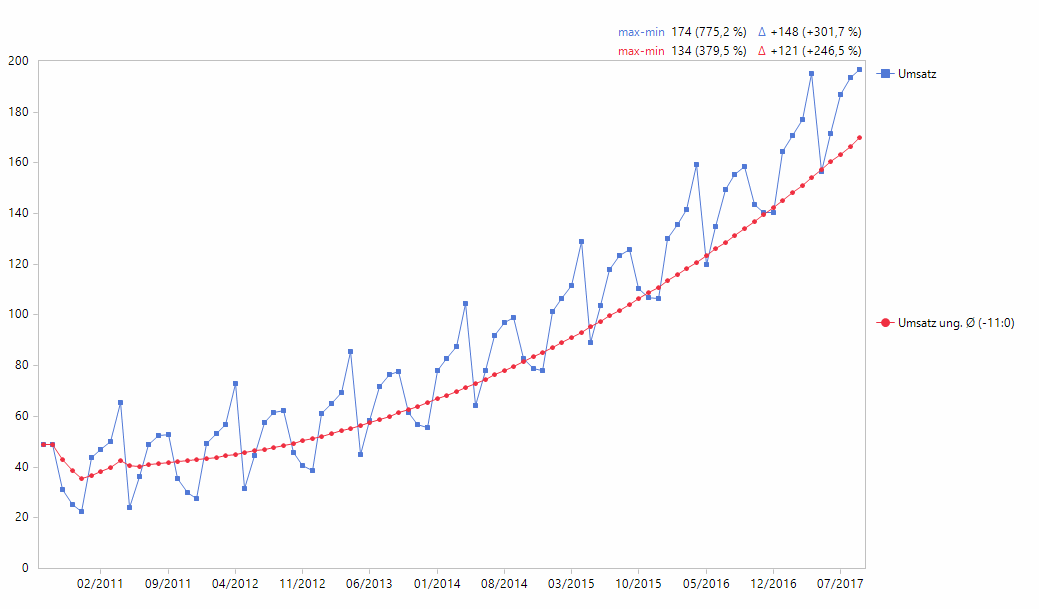
Die monatlichen Umsatzdaten mit dem nicht zentrierten Durchschnitt
Im flachen Bereich bis etwa Ende 2012 sieht die geglättete Kurve einwandfrei aus, aber mit dem einsetzenden Wachstum hinkt der einseitig berechnete Durchschnitt den tatsächlichen Werten immer mehr hinterher.
Versuchen wir es mit einem zentrierten Durchschnitt analog zu oben: Wir verwenden als Aggregation den Mittelwert der letzten 13 Monate, nehmen aber als Referenzpunkt den neu erstellten Zeitanalysewert “in 6 Monaten” und das Fenster deckt somit den Bereich (-6:+6) ab. Dergestalt definiert wird der geglättete Wert bspw. für März 2017 als Durchschnitt der Werte von September 2016 bis September 2017 berechnet.
Wie sieht das Ergebnis aus?
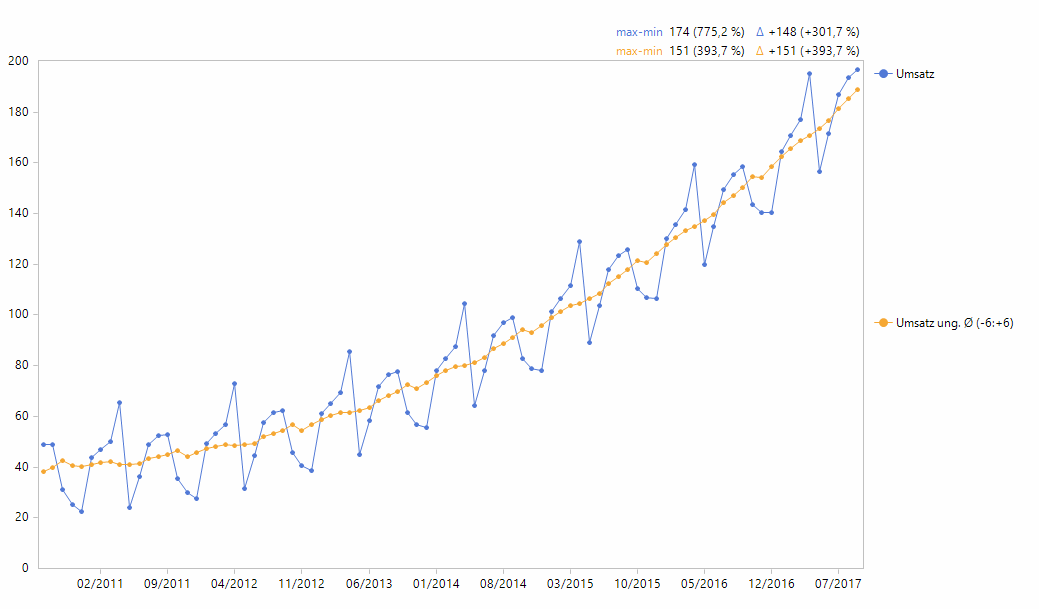
Die monatlichen Umsatzdaten mit dem zentrierten Durchschnitt
Nun verläuft die geglättete Kurve zwar mitten durch die Punkte, ist aber längst nicht mehr so schön glatt wie die Kurve im einfachen Ansatz. Woran liegt es?
Werfen wir doch einen Blick auf einen Ausschnitt der Zeitreihe:
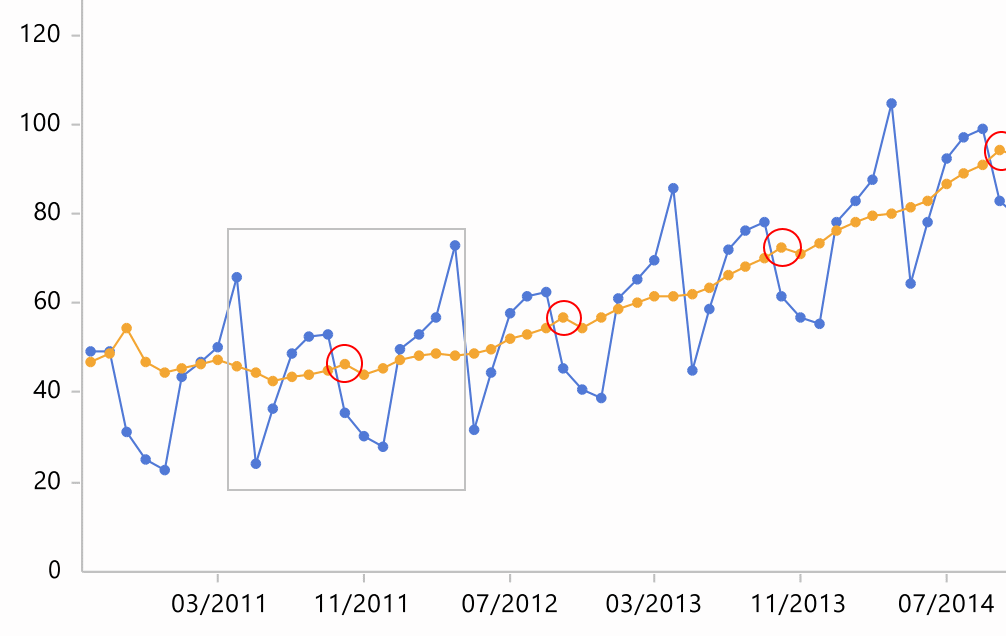
Ausschnitt: Relevante Werte für Oktober 2011
Die Kreise kennzeichnen die geglätteten Werte jeweils für den Oktober; sie scheinen immer etwas zu hoch gelegen. Betrachtet man das Fenster der relevanten Werte etwa für Oktober 2011, so gehören die beiden äußeren Spitzenwerte zu April 2011 und April 2012. D. h., die hohen Aprilwerte gehen in diesen Durchschnittswert gleich zweimal ein. Diese doppelte Gewichtung zieht den Durchschnittswert nach oben.
Für den benachbarten Novemberwert zur rechten Seite gilt Ähnliches, aber mit umgekehrtem Vorzeichen. Da Maiwerte immer sehr niedrig ausfallen und diese für den Novemberdurchschnitt doppelt eingehen, fällt der geglättete Wert für November tendenziell niedriger aus.
Die Problematik tritt immer bei einer geraden Anzahl von Perioden (hier 12 Monate) im Saisonverlauf auf. Die Statistik behilft sich mit einem gewichteten Mittelwert, der den beiden Werten am Rand nur ein halbes Gewicht gibt. Die Berechnung lautet:
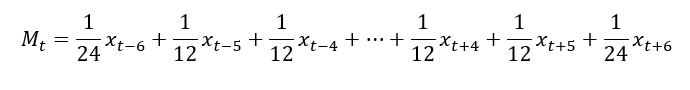
Formel für den gewichteten Durchschnitt
Diese Möglichkeit des gewichteten Durchschnitts ist (noch?) nicht in DeltaMaster eingebaut, aber versuchen wir doch einfach folgendes. Zunächst definieren wir einen Durchschnitt der Länge 12 (kein Monat doppelt, also glatter Verlauf!) und hängen ihn am Referenzelement “in 5 Monaten” auf. D. h. dieser Durchschnitt deckt den Bereich (-6:+5) ab und hinkt der tatsächlichen Entwicklung leicht hinterher, in einer Formel ausgedrückt lautet er:
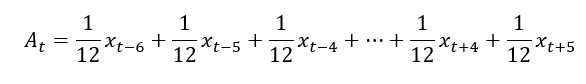
Formel für leicht verzögerten Durchschnitt
Ein weiterer Durchschnitt hat ebenfalls die Länge 12 und besitzt das Referenzelement “in 6 Monaten”. Dieser Durchschnitt eilt mit dem Bereich (-5:+6) der tatsächlichen Entwicklung leicht voraus:
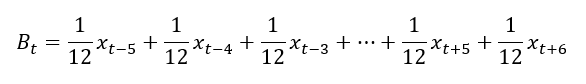
Formel für leicht vorauseilenden Durchschnitt
Die geglätteten Kurven für diese beiden Fälle sehen folgendermaßen aus:
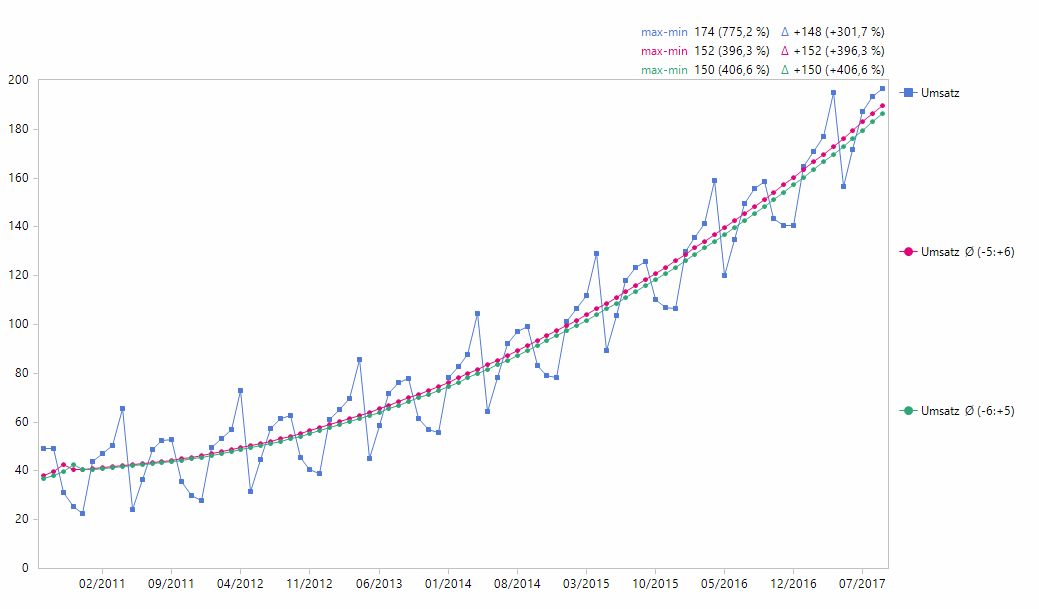
Zwei glatte Durchschnittskurven
Beide Kurven sehen gut aus, die rote, vorauseilende liegt leicht zu hoch, die grüne, etwas hinterherhinkende liegt leicht zu niedrig.
Es gibt aber einen Weg, die optimal geglättete Kurve, die in der Statistikliteratur bevorzugt wird, zu erhalten.
Wenn man ein berechnetes Element als Mittelwert der beiden Größen anlegt, stellt man fest, dass sich der Wert der statistischen Formel ergibt:
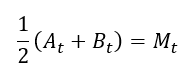
Den Anforderungen der Statistik Genüge getan
Bildet man nun wieder einen Filterwert mit diesem berechneten Element, so lässt sich ein überzeugendes Ergebnis bestaunen:
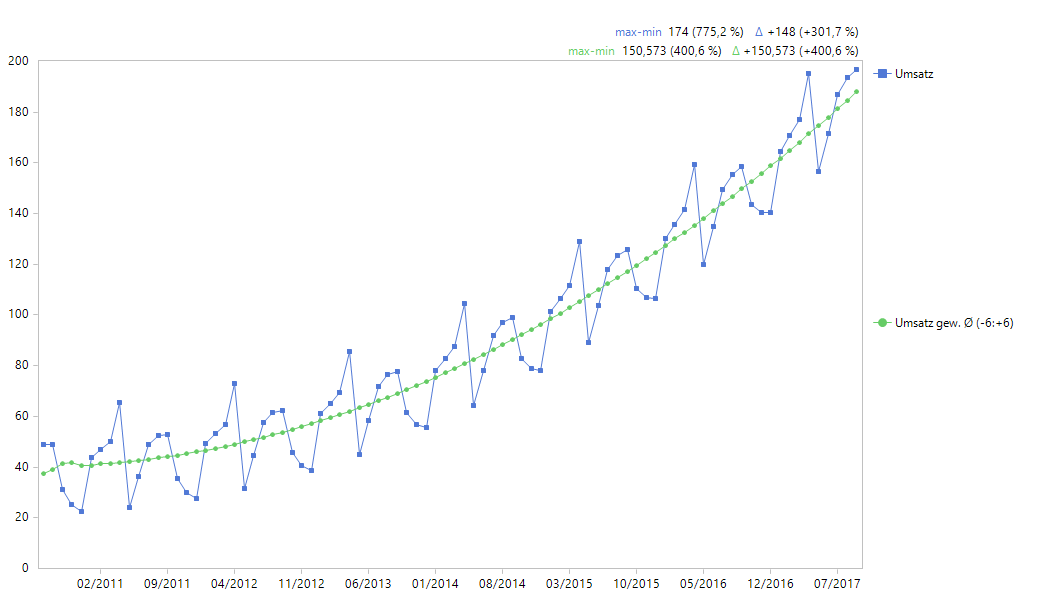
Glatte Durchschnittskurve durch die Umsatzwerte
Bis auf minimale Knicke am linken Rand, die daraus resultieren, dass hier die Zeitreihe beginnt und nicht alle Werte innerhalb des Glättungsfensters vorliegen, verläuft die Kurve äußerst glatt und gleichmäßig mitten durch die Umsatzwerte.
Rekapitulieren wir kurz: Um so weit zu kommen, haben wir einen Zeitanalysewert “in 5 Monaten” und eine gleitende Mittelwertaggregation der Länge 12 mit dem passenden Referenzelement “in 5 Monaten” definiert. Die hierauf aufbauende Glättung liefert bereits zufriedenstellende Ergebnisse.
Alternativ hätten wir einen Zeitanalysewert “in 6 Monaten” und die dazu passende Mittelwertaggregation definieren können, mit einem qualitativ ähnlich guten Ergebnis.
Optimal wird unsere Glättung, wenn wir beide Ergebnisse kombinieren und schließlich ein berechnetes Element als Mittelwert der beiden letztgenannten Mittelwertaggregationen definieren.
Dieser Aufwand wird pro Sitzung genau einmal betrieben, anschließend lassen sich alle in Frage kommenden Analysewerte mit dem berechneten Element als Filterwert definieren.
Natürlich lassen sich die Werte der dargestellten Trendkurven auch in Grafischen Tabellen ausweisen und – wie alle anderen Analysewerte auch – weiterverarbeiten.
Quelle:
- Datenbasis: Deutscher Wetterdienst für die Wetterdaten Nürnberg, Tageswerte abgerufen für den Zeitraum vom 12.3.2017 bis zum 24.7.2018, als geglättete Werte weiterverarbeitet