Eine geeignete Visualisierung von Zeitspannen hilft, den Ablauf von Teilprozessen in einem Projekt besser zu verstehen. In DeltaMaster schlummert bereits eine Möglichkeit zur Umsetzung – in einem durchaus überraschenden Kontext!
Visualisierung von Zeitspannen in Projekten
Zeitspannen in Projekten
Besonders in der Projekt- oder Ablaufplanung oder im Projektcontrolling möchte man den Überblick über die zeitliche Abfolge von einzelnen Teilprojekten behalten. Etabliert sind etwa Gantt-Diagramme oder die Methode des kritischen Pfades (CPM: Critical Path Method).
Auch wenn wir in unserer Business-Intelligence-Software DeltaMaster diese Ansätze nicht mit eigenen Modulen unterstützen, können wir die Quintessenz der Darstellungen – also Beginn und Ende und damit Dauer von Vorgängen inklusive etwaiger Pufferzeiten – durchaus übersichtlich wiedergeben.
Der heutige Blogbeitrag ist sehr forschungsnah ausgerichtet und untersucht den möglichen Einsatz bereits bestehender Module. Welche das sind? Lassen Sie sich überraschen!
Ein einfaches Beispiel
Hier nehmen wir an, dass in einem Gesamtprojekt zwei Teilprojekte vorliegen, die ihrerseits aus zu bearbeitenden Aufträgen bestehen, die sich wiederum aus Einzelaufträgen zusammensetzen. Für diese Einzelaufträge sind Anfang und Ende in Tagen ab Anfang des Gesamtprojektes gegeben:
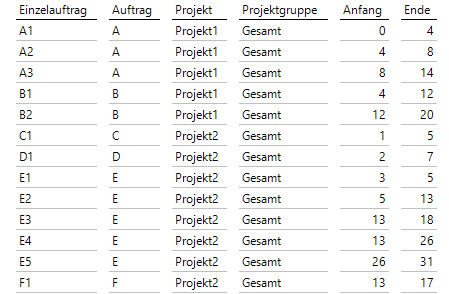
Anfang und Ende von Einzelaufträgen
Bei der Modellierung haben wir hier als Datenquelle Microsoft Excel/MDX Analytics gewählt. Für unsere, weiter unten präsentierte Lösung benötigen wir nämlich MDX-Konstrukte, sodass eine rein relationale Lösung leider nicht funktioniert.
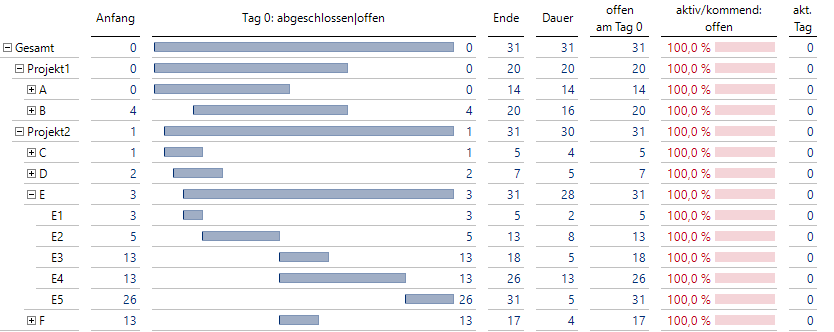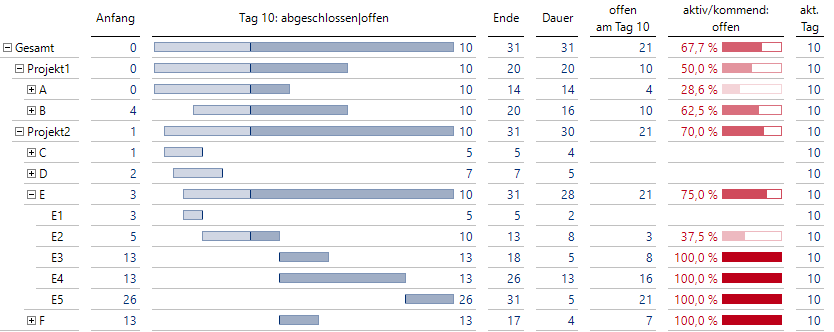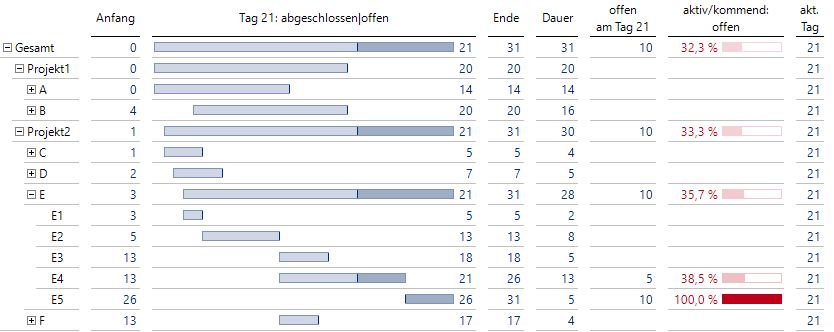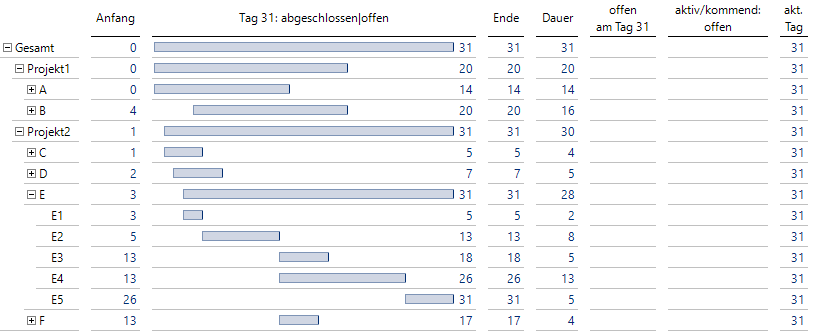
Bei der Aggregation der Kennzahlen in der Projekthierarchie wählen wir für die Kennzahl “Anfang” den Typ Minimum und für “Ende” Maximum, dann ergeben sich automatisch die korrekten Zeitspannen auch für die höheren Ebenen. In einer Grafischen Tabelle sehen wir dann diese Darstellung:
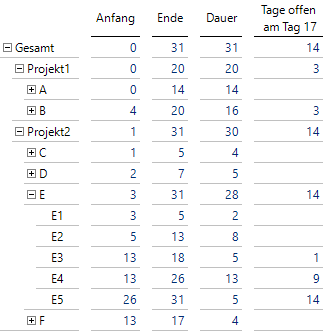
Anfang und Ende auf allen Ebenen
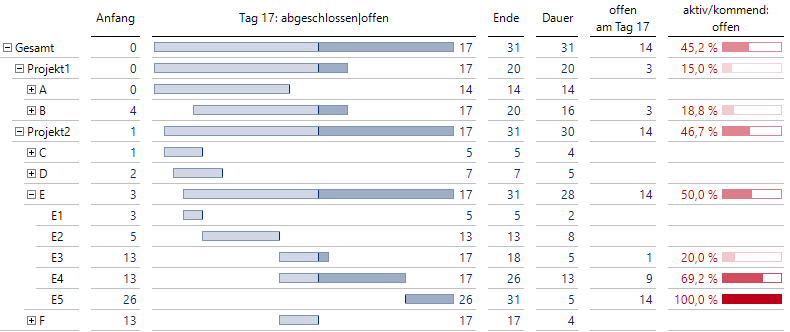
Zum Beispiel erkennen wir bei Auftrag E, dass der Anfang mit Tag 3 durch Teilauftrag E1 und das Ende durch die 31 des Teilauftrags E5 bestimmt werden. Auch das Ende von Projekt 2 wird von Auftrag E abgeleitet, während der Anfang hier durch Auftrag C festgelegt wird.
Auf allen Ebenen sind somit Anfang und Ende definiert, darüber hinaus lassen sich nun Zeitdauern als Differenz Ende – Anfang berechnen.
Ist der aktuelle Tag gegeben, unter der Annahme eines stets aktualisierten Zeitplans, kann berechnet werden, ob und wie viele Tage bei den einzelnen Elementen noch offen sind.
Nun wäre es aber nützlich, beispielsweise mit Balken die Zeitspanne zwischen Anfang und Ende auch grafisch darzustellen. Solche in der Zeit freischwebenden Balken, die ja nun von zwei Kennzahlen abhängen, gibt es aber nicht in DeltaMaster, oder?
Weit gefehlt! Wir haben eine Möglichkeit, einen waagerechten Balken frei zu positionieren: Zur Visualisierung von Zeitspannen greifen wir auf den bereits implementierten Boxplot zurück!
Boxplots
Üblicher Einsatz von Boxplots, wie man ihn kennt
Normalerweise wird der Boxplot eingesetzt, um eine einprägsame und gleichzeitig schlanke Darstellung der Verteilung einer Kennzahl auf den Elementen einer Dimensionsebene zu erhalten. Schauen wir zum Beispiel auf die Liste aller Städte beim Statistischen Bundesamt mit Angabe u. a. der Einwohnerzahl.
Um Boxplots einsetzen zu können, müssen wir die sechs univariaten statistischen Analysewerte – wie auch der Hinweis in der Definition im folgenden Screenshot verrät – Anzahl (exkl. Nullwerte), Minimum, Unteres Quartil (25%), Median, Oberes Quartil (75%) und Maximum anlegen. Dazu benötigen wir hier eine Kennzahl Einwohner und die Ebene der Städte, die über eine laufende Nummer durchiteriert wird:
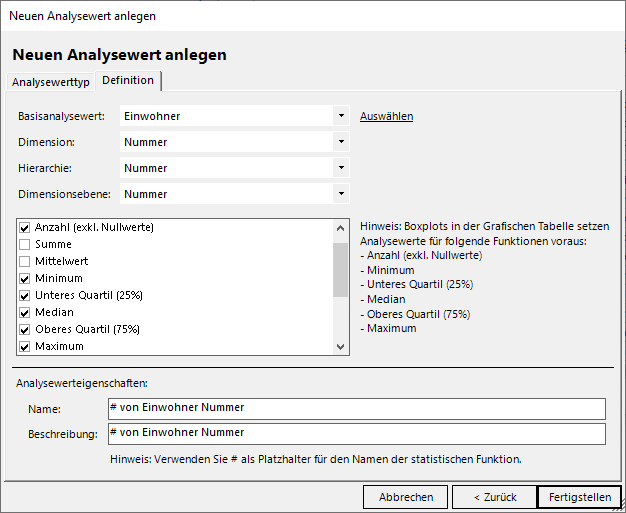
Univariate statistische Analysewerte werden auf der Ebene der internen Städtenummer definiert
Im Folgenden werde ich mich hier aus didaktischen Gründen auf Städte unterhalb von 100.000 Einwohnern beschränken.
Anmerkung am Rande: Während Großstädte mindestens 100.000 Einwohner haben müssen, gibt es anscheinend für Städte unterhalb von 100.000 Einwohnern keine entsprechende Bezeichnung; Kleinstädte liegen jedenfalls zwischen 5.000 und 20.000 Einwohnern. Angeblich heißen Städte zwischen 20.000 und 100.000 Einwohnern Mittelstädte und unterhalb von 5.000 Einwohnern reden wir von Landstädten.
Weiterhin hätte ich gerne die PLZ den Bundesländern zugeordnet, aber hier habe ich keine vertrauenswürdige Webseite entdecken können, deren Link ich ruhigen Gewissens hätte angeben können. Deshalb habe ich ersatzweise die PLZ nach der 1. Ziffer gruppiert.
Der Boxplot im Beispiel
Ziehen wir in einer Grafischen Tabelle den definierten Medianwert auf die Spaltenachse, können wir im Editiermodus unter Grafik den Boxplot aktivieren. Alternativ können wir den Boxplot auch beim Mittelwert zeigen, den wir hier aber nicht definiert hatten:
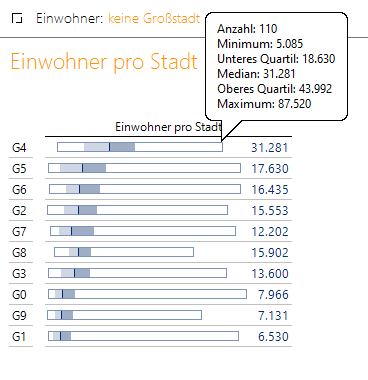
Boxplot der Kleinstädte nach Gebieten
Hier sieht man die idealtypische Darstellung eines Boxplots. Die 5 Werte Minimum, Unteres Quartil (25%), Median, Oberes Quartil (75%) und Maximum sind sichtbar und Flächen zwischen zwei aufeinanderfolgenden Werten sind eingefärbt. Zum Beispiel ist die Fläche zwischen Minimum und unterem Quartil weiß, zwischen unterem Quartil und dem Median hellblau (bei einem positiven Faktor des Analysewerts), zwischen Median und oberem Quartil dunkelblau und zwischen oberem Quartil und Maximum wieder weiß.
Der Median wird durch einen eigenen dunklen Strich extra betont.
Bei einer großen Anzahl von Objekten (hier von Städten) ist es nicht falsch zu sagen, dass jeweils ca. 25 % der Daten in jede der vier Flächen fallen.
Bei unserem Beispiel haben Nicht-Großstädte mit einer mit 4 beginnenden PLZ (NRW und Niedersachsen) tendenziell mehr Einwohner; mit einer 1 am Anfang (z. B. Brandenburg oder Mecklenburg-Vorpommern) fällt die Einwohnerzahl deutlich kleiner aus: Die Hälfte aller Fälle liegt unter ca. 6.500 Einwohnern.
Definition von Median und Quartilen
Der berechnete Median gehört zum MDX-Funktionsumfang und wird somit von der Engine bereits fertig geliefert. Bei einer ungeraden Anzahl von Elementen entspricht er dem mittleren Element der sortierten Liste. Gibt es zum Beispiel 101 Werte, so ist der Median identisch zum 51. Wert.
Ist die Anzahl gerade, wird für den Median der Mittelwert der beiden zentralen Elemente genommen. Liegen etwa 100 sortierte Werte vor, so gehen Wert 50 und 51 in den Mittelwert ein.
Rob J. Hyndman hat in seinem Artikel “Sample Quantiles in Statistical Packages”, veröffentlicht November 1996 im “The American Statistician 50:361-365”, neun verschiedene Varianten beschrieben, Quantilsschätzer zu berechnen. Quantile sind allgemeiner als Quartile und nicht auf 25% oder 75% beschränkt, sondern können für jede beliebige Prozentzahl berechnet werden.
Glücklicherweise setzen wir bei uns eine Variante ein, die eine nun für uns sehr vorteilhafte Eigenschaft besitzt.
Liegen in einer Ebene nämlich exakt 5 Elemente vor und sortieren wir diese aufsteigend nach der Kennzahl, also beispielsweise A ≤ B ≤ C ≤ D ≤ E, dann entsprechen diese 5 Werte genau den Größen Minimum, Q25, Median, Q75 und Maximum.
Dass der kleinste Wert dem Minimum entspricht und der größte Wert dem Maximum, ist klar. Da 5 ungerade ist, wird der Median aus dem mittleren, dritten Element C abgelesen. Bis hierhin ist eine Übereinstimmung also keine Überraschung.
Die Verwendung der gewählten Variante führt nun dazu, dass auch die beiden restlichen Werte B und D den Quartilen Q25 und Q75 entsprechen. Für die meisten anderen Varianten gilt diese Entsprechung nämlich nicht.
Boxplots zur Visualisierung von Zeitspannen
Normalerweise würde man bei nur 5 Werten nicht zwingend als Erstes an den Boxplot denken, um eine Verteilung der Werte zu beschreiben.
Das haben wir hier aber auch gar nicht vor; wir steuern durch passende Vergabe von Werten auf den 5 Elementen einer Hilfsdimension das Aussehen der Grafik und sind somit überhaupt nicht an einer Verteilung interessiert.
Dabei profitieren wir von der Tatsache, dass eine Fläche verschwindet, wenn die benachbarten Werte identisch sind. Zum Beispiel verschwindet die erste weiße Fläche, wenn A = B gilt, und die hellblaue Fläche, falls B und C identische Werte aufweisen.
Für jedes der Paare (A, B), (B, C), (C, D) und (D, E) kann die Fläche verschwinden oder nicht. Insgesamt gibt es somit 2 * 2 * 2 * 2 = 16 mögliche Kombinationen.
Diese Kombinationen habe ich in der folgenden Tabelle zusammen mit einem Beispieldatensatz aus 5 Elementen aufgeführt. Hier ist immer A = 1 und E = 5, aber diese Zahlen stehen hier natürlich nur stellvertretend, um die qualitativ möglichen Fälle aufzulisten:
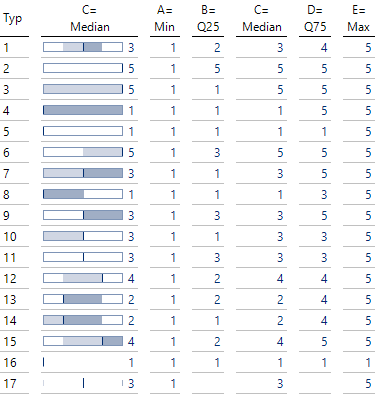
Bausteine zur Visualisierung von Zeitspannen
Typ 2 und Typ 5 unterscheiden sich durch die Lage des Medianstrichs, der einmal am rechten und einmal am linken Ende zu finden ist.
Typ 16 ist degeneriert, da alle Flächen verschwinden. Wenn weniger als 5 Werte vorliegen (Typ 17), werden keine Balken mehr gezeichnet, sondern nur noch Striche. Hier gäbe es noch weitere Möglichkeiten, die wir aber in diesem Blogbeitrag nicht verfolgen.
Beispiele
Technisches Vorgehen
Wir legen eine Hilfsdimension mit 5 Elementen 1 bis 5 (oder A, B, C, D und E) an. Weiterhin brauchen wir die oben erwähnten sechs univariaten statistischen Analysewerte einer Kennzahl über die Ebene dieser 5 Elemente. Die Kennzahl selbst definieren wir in Abhängigkeit vom vorliegenden der 5 Elemente und den Start- und Endwerten eines Projekts, sowie des aktuellen Tags.
Start- und Endwerte des Projekts müssen immer vorliegen und abrufbar sein, wenn wir intern über die 5 Elemente iterieren. Das genaue Vorgehen hängt von der Modellierung ab, aber Filterwerte sind hier oft sehr nützlich und sichern ab, dass Start- und Endzeiten bei der Iteration über die Elemente der Hilfsdimension genutzt werden können.
Wir vergeben die 5 Werte an die Elemente bereits sortiert. Das ist keine notwendige Voraussetzung, erleichtert aber den Überblick.
Gantt-Diagramm
Spinnen wir einmal das anfangs erwähnte Beispiel mit dem hierarchischen Projektaufbau weiter. Von den 15 möglichen Typen finden wir hier die folgenden 3 Typen besonders passend:
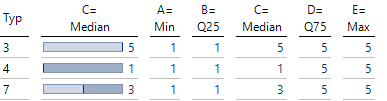
Passende Bausteine für Gantt-Diagramme
Typ 3 soll für ein abgeschlossenes Projekt stehen, Typ 4 für ein noch kommendes und Typ 7 für ein gerade laufendes. Die Rolle der 1 übernimmt der Startzeitpunkt und für die 5 wird der Endzeitpunkt eingesetzt. Wie man sieht, sind die Werte für A und B bei allen 3 Typen gleich dem Startwert und für D und E immer gleich dem Endwert.
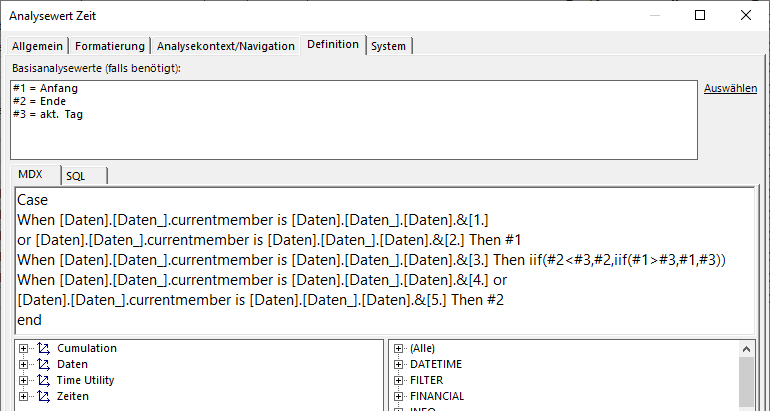
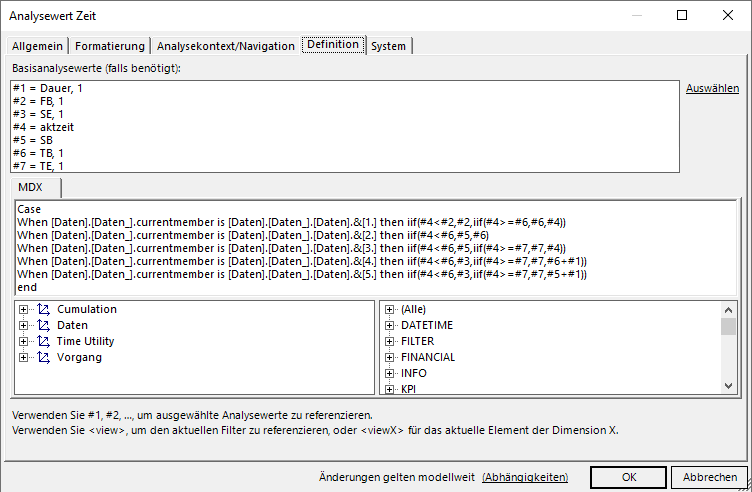
Die MDX-Definition der Kennzahl, die in die sechs univariaten statistischen Analysewerte eingeht, lautet deshalb:
Kennzahldefinition
Hier wird den ersten beiden Elementen immer der Startwert und den letzten beiden Elementen immer der Endwert zugeordnet.
Für das dritte, mittlere Element kommt eine Fallunterscheidung zum Tragen. Liegt das Projekt in der Zukunft, wird hier der Projektstart eingetragen, ist das Projekt abgeschlossen, wird das Projektende eingesetzt und wenn es gerade läuft, steht hier der aktuelle Tag.
Schauen wir nun auf unsere Grafische Tabelle von oben, aber diesmal mit zusätzlicher Visualisierung des Projektfortschritts:
Projektstände werden nun deutlich einfacher erfasst
Durch die Visualisierung von Zeitspannen können wir nun Projektstände ohne Schwierigkeiten erfassen. Die Farbtrennung hell/dunkel erlaubt eine deutlich einfachere Orientierung, wo man sich im Projekt befindet.
Für noch laufende Projekte kann bei Bedarf der noch offene Anteil des Projekts berechnet und ausgegeben werden.
Die folgende Animation (öffnen Sie das Bild am besten in einem neuen Tab oder Fenster, falls sich hier nichts bewegt!) zeigt die Darstellung während des Projektablaufes:
Visualisierung von Zeitspannen in der Gantt-Variante
Methode des kritischen Pfades (CPM: Critical path method)
Bei der Methode des kritischen Pfades existieren Abhängigkeiten zwischen Projekten. Damit ein bestimmtes Projekt beginnen kann, müssen oft ein oder mehrere andere Projekte abgeschlossen sein.
Manche Projekte befinden sich auf dem kritischen Pfad. Verzögerungen bei solchen Projekten erhöhen die Gesamtdauer.
Andere Projekte haben einen Puffer und leichte Verzögerungen lassen sich noch abfangen. Für jedes Teilprojekt existiert ein Intervall frühester/spätester Anfang. Bei Projekten auf dem kritischen Pfad sind beide Werte identisch.
Die Ermittlung des kritischen Pfads ist hier aber nicht Thema. Wir setzen voraus, dass die relevanten Zeitpunkte bereits berechnet wurden und als bekannt vorausgesetzt werden können.
Die folgenden Varianten werden sich zur Visualisierung von Zeitspannen bei der Methode des kritischen Pfades als nützlich erweisen:
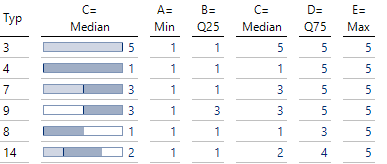
Nützliche Balkentypen für CPM
Zusätzlich zu den bereits erwähnten Typen 3, 4 und 7 sind die Typen 9, 8 und 14 neu dazugekommen.
Typ 9 wollen wir für ein kommendes Projekt verwenden, das einen Puffer besitzt. Hier wird mit dem dunklen Teilbalken die späteste Durchführung dargestellt.
Typ 8 setzen wir zum Zeitpunkt des Beginns des Projektes ein. Mit Beginn des Projekts wandert der Puffer ans Ende, da nun interessiert, bis wann wir das Projekt abgeschlossen haben müssen, und ob Verzögerungen einer bestimmten Größe kritisch sind. Typ 14 setzen wir ein, wenn ein solches Projekt mit Puffer bereits eine Weile läuft.
Beispiel einer CPM-Anwendung
Für die Daten zum Beispiel eines CPM-Netzplans bei Wikipedia sieht die Darstellung vor Beginn des Gesamtprojektes folgendermaßen aus:
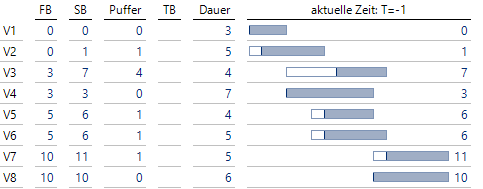
Projekte mit/ohne Puffer vor Projektbeginn
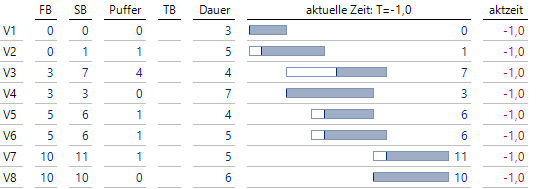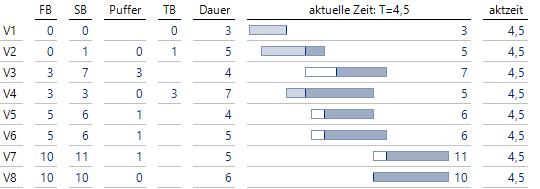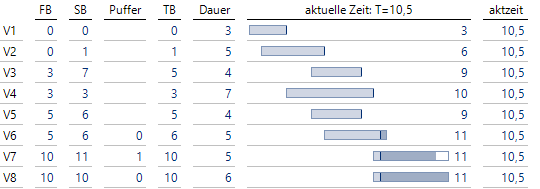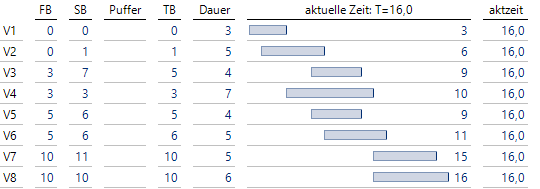
Angegeben sind immer die Planwerte frühester Beginn (FB), spätester Beginn (SB) und die Istwerte – falls vorhanden – tatsächlicher Beginn (TB). Die Vorgänge V1, V4 und V8 liegen auf dem kritischen Pfad, die anderen Vorgänge besitzen einen Puffer.
Richten wir einmal das Augenmerk auf Vorgang V3. Zum Zeitpunkt T = 4 wurde eine Einheit des Puffers aufgebraucht, das Projekt hat noch nicht begonnen:

V3 hat zum Zeitpunkt T = 4 noch nicht begonnen
Hier haben wir den linken Rand des Puffers angepasst, da nicht genutzter Puffer der Vergangenheit keine Rolle mehr spielt. Bereits begonnene Projekte sind nun durch den tatsächlichen Beginn (TB) gekennzeichnet. Hier wechseln wir in der Darstellung von Plan- zu Istwerten.
Zum Zeitpunkt T = 5 beginnt Vorgang V3:
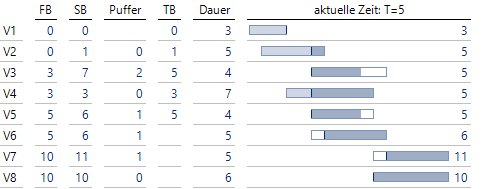
V3 beginnt zum Zeitpunkt T = 5, der Puffer wandert ans Ende
Mit Projektbeginn von V3 wird der verbleibende Puffer der Länge 2 ans Ende gestellt.
Definition der Kennzahl
Die Definition der Kennzahl, die für den Boxplot eingesetzt wird, unterscheidet einige Fälle, die von FB, SB, TB, Dauer und der aktuellen Zeit abhängen. In der gezeigten Variante wird angenommen, dass etwaige Verzögerungen, die das Einhalten der Gesamtprojektdauer verhindern, zu einer sofortigen Aktualisierung der Planwerte noch nicht begonnener Teilprojekte führen.
Es ist hilfreich, sich die Fälle aufzuschreiben und die gewünschten Werte auf der Hilfsdimension festzulegen:
Diese 4 Konstellationen können entstehen
Bei dieser Definition wurde angenommen, dass wir TB und TE mit sehr hohen, im Zeitverlauf nicht erreichbaren Werten initialisiert haben. Im Laufe des Projekts überschreiben wir diese dann mit den tatsächlichen Werten.
Nun lässt sich die Kennzahl leicht definieren:
Definition der Kennzahl
Die folgende Animation (falls Sie diese nicht sehen, öffnen Sie am besten das Bild in einem neuen Tab oder Fenster!) zeigt den Ablauf während des Projektes:
Visualisierung von Zeitspannen im Laufe des Projekts
Man kann sich Varianten der Darstellung vorstellen, bei denen Plan und Ist simultan gezeigt und Abweichungen betont werden. Mit dem Baukasten der 15 nutzbaren Typen lassen sich Projekte mit Beginn, Ende, Dauer und Pufferzeiten jedenfalls leicht nachvollziehbar darstellen.
Die Grundidee dieses Blogbeitrags ließe sich noch auf andere Anwendungen übertragen – aber das überlasse ich lieber Ihrer Phantasie.
Quelle der Einwohner-Daten
Städte (Alle Gemeinden mit Stadtrecht) nach Fläche, Bevölkerung und Bevölkerungsdichte am 31.12.2019, URL: https://www.destatis.de/DE/Themen/Laender-Regionen/Regionales/Gemeindeverzeichnis/Administrativ/05-staedte.html, Open Data bei DESTATIS – Statistisches Bundesamt, gruppiert nach 1. Ziffer und Großstädten/restliche Städte.
Datenlizenz Deutschland – Namensnennung – Version 2.0 (Lizenztext unter https://www.govdata.de/dl-de/by-2-0)