20 Bissantz-Mitarbeiter durften es unter Wettbewerbsbedingungen am eigenen Leibe erfahren: Die typografisch skalierten Zahlen der Bissantz’Numbers schlagen Diagramme und Grafiken – ausgerechnet dort, wo diese eigentlich Vorteile haben sollten – im schnellen Verständnis von Zahlen.
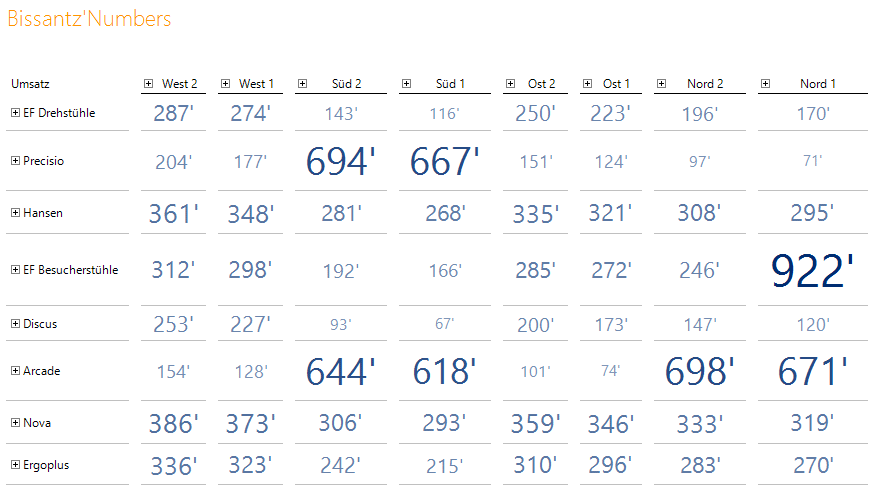
Seit der Version 6.1.6 bietet DeltaMaster die Bissantz’Numbers bzw. Zahlogramme als Grafiktyp für Grafische Tabellen an. Die Idee ist dabei so einfach wie genial: Je größer der Wert, desto größer wird die Zahl auch dargestellt. Dadurch reicht bereits ein flüchtiger Blick auf die Tabelle, um allein schon durch peripheres Sehen zu “spüren”, wo die Musik spielt:
Ohne Anstrengung erkennt man beispielsweise in obiger Tabelle, dass es einen herausragenden Wert 922 Tsd. gibt (EF Besucherstühle, Nord 1), dass Arcade in den Süd- und Nord-Regionen und Precisio nur in den Süd-Regionen noch beachtenswerte Umsätze erzielt haben, oder dass Nova im Vergleich zu Discus durchgehend höhere Umsätze erzielt.
Hier in diesem Beitrag steht die halb spielerische, halb wissenschaftliche Beschäftigung mit den Zahlogrammen im Vordergrund. 20 Mitarbeiterinnen und Mitarbeiter aus allen Abteilungen mit unterschiedlicher Vertrautheit zum Produkt, aber gleichermaßen hohem Ehrgeiz mussten unter zeitlichem Stress die jeweils 3 größten Zahlen in zufällig erzeugten Tabellen mit jeweils 6 Zeilen und 6 Spalten, also 36 Werten in absteigender Reihenfolge anklicken. Diese Aufgabe passt zum Ziel, die größten Positionen schnell zu erfassen.
Eine andere hier nicht näher untersuchte Fragestellung könnte z. B. sein, die Anzahl der Felder mit sehr großen oder mittelgroßen Beiträgen instinktiv in kurzer Zeit zu erfassen. Denkbar wären auch Tests zur Überprüfung, ob die gesehenen Werte auch verarbeitet wurden und abgerufen werden können.
Wir haben uns hier für das Auffinden der TOP 3 im Kontext der Tabelle entschieden, auch deshalb, weil mit der benötigten Zeit bis zur richtigen Lösung ein einfach zu messendes Kriterium zur Verfügung steht.
Bei den original Bissantz’Numbers, bei denen neben der Fontgröße auch die Farbintensität mit wachsendem Wert zunimmt, sieht eine richtig gelöste Aufgabe folgendermaßen aus (bitte klicken Sie auf die Grafik für eine vergrößerte Darstellung):

Aufgabe dank typografischer Skalierung in 3.7 Sekunden gelöst!
Hatte jemand die falschen drei Werte angeklickt, wurden nach einem kurz eingeblendeten Hinweis und einem über Kopfhörer eingespielten motivierenden Aufstöhnen (welches manchmal auch direkt vom Probanden zu kommen schien) dieselben Werte eingespielt, so lange, bis endlich die richtige Lösung gefunden war.
Speziell die Darstellung mit gleich groß skalierten Ziffern führte in manchen Fällen zur Verzweiflung, wenn dem Mitarbeiter oder der Mitarbeiterin partout nicht klar wurde, warum denn die angeklickten drei Werte nicht der gesuchten Lösung entsprechen sollen:
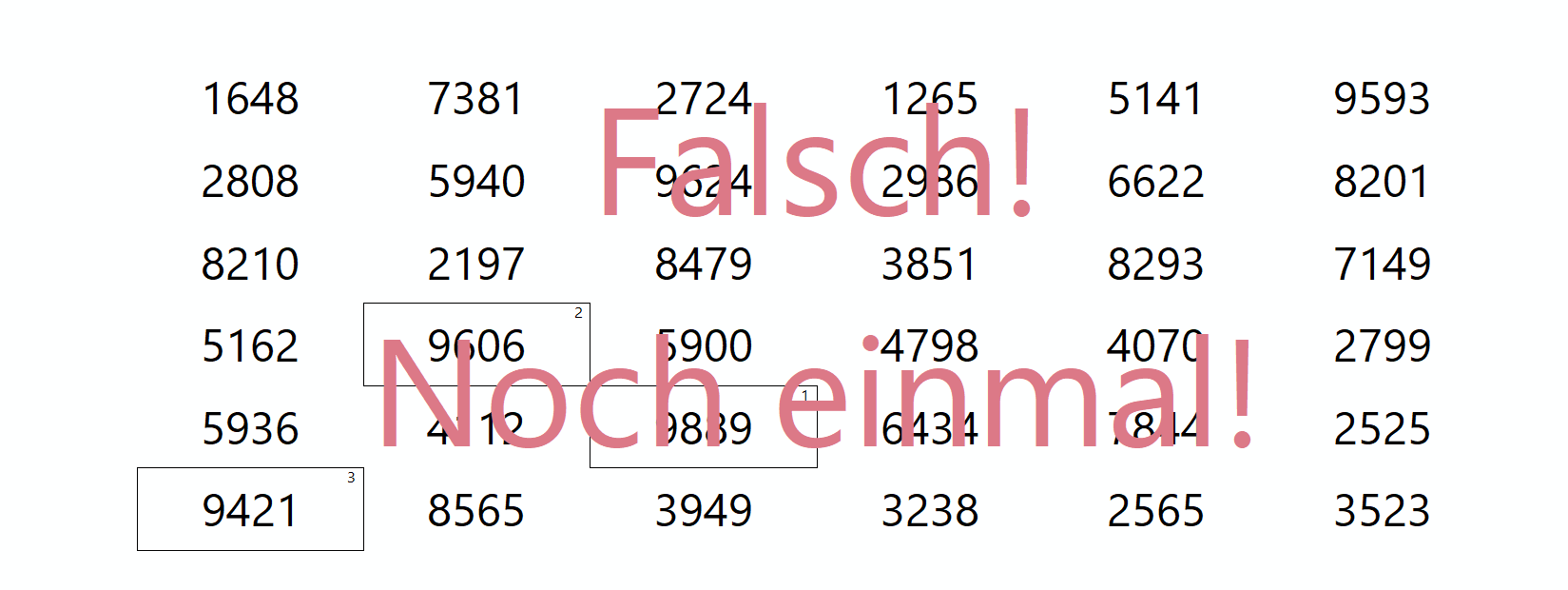
Nahe der Verzweiflung wegen fehlender Führung durch grafische Elemente
Fehlerhafte Eingaben hatten bei den “normalen” Zahlen auffallend häufig eine Vorwärts-Rückwärts-Abstandsjustierung des Mitarbeiters zum Bildschirm zur Folge.
Insgesamt gab es drei grafische Darstellungen, neben den beiden genannten noch die Präsentation der Tabelle mittels Kreisen, die im Falle der hier gegebenen Kreuztabelle anderen Optionen wie Säulen oder Balken vorzuziehen ist:

Wie werden sich Grafiken schlagen? Wir testen mit Kreisen!
Jede dieser drei Hauptvarianten wurde noch in zwei Variationen präsentiert: Einmal erscheinen die Schriften in Blau mit Farbintensität, einmal in schnödem Einheitsschwarz.
Die drei Hauptvarianten wurden im sich wiederholenden Zyklus Bissantz’Numbers -> Gleich groß -> Kreise -> Bissantz’Numbers -> … gezeigt, die Schriften abwechselnd in Blau -> Schwarz -> Blau -> …; nach 6 Iterationen waren somit alle 6 möglichen Kombinationen einmal zu sehen. Dieser Block wurde dann 3-mal wiederholt, sodass insgesamt 18 Aufgaben in einem Durchlauf zu lösen waren.
Im folgenden Video ist zur besseren Illustration ein Block mit 6 Iterationen zu sehen, hier sogar unter Einsatz des Eyetrackers, der aber nur für dieses Video zum Einsatz kam:
Sie sehen gerade einen Platzhalterinhalt von YouTube. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Fiebern Sie mit und erleben Sie die Testsituation wie unsere Probanden!
Die meisten Probanden standen für drei Durchläufe zur Verfügung:
Im ersten Durchlauf mit 18 Aufgaben waren die Zahlen einfach gewählt, sodass nur wenige sehr große Zahlen erzeugt wurden. Im zweiten Durchlauf wurden dann tendenziell mehr größere Zahlen generiert, sodass die Identifizierung der TOP 3 schwieriger zu bewerkstelligen war. Der dritte Durchlauf war identisch zum ersten, nur wurde für die Darstellung “Gleich große Zahlen” ein höherer Wert für die Schriftgröße gewählt.
Soweit zur Gestaltung des Versuchsaufbaus. Versuchen wir nun, die Erkenntnisse strukturiert zusammenzufassen.
Die erste Erkenntnis ist, dass die Teilnehmer sehr unterschiedlich an die Aufgabe herangingen: Entweder wurde stürmisch geklickt und dementsprechend häufiger korrigiert oder es wurde wohlüberlegt das Gesamtbild betrachtet, bevor dann entschlossen die Klicks gesetzt wurden. Natürlich gab es auch die Fälle, bei denen trotz reiflicher Überlegung nicht das korrekte Tripel ausgewählt wurde.
Schauen wir einmal auf die Wirkung der Farbintensität für den Fall gleich großer Fontgrößen. Die folgende Grafik zeigt die vier Varianten kleine und große Schrift für die beiden Fälle mit und ohne Variation der Farbintensität:

Hilft die Farbintensität bei der Orientierung?
Wir betrachten nun die Wirkung der Intensität bei den 12 Personen, die alle drei Durchläufe absolviert haben. Der Einfachheit halber reicht hier eine gemeinsame Boxplotdarstellung mit 12 x 3 =36 Messungen pro Zeile:
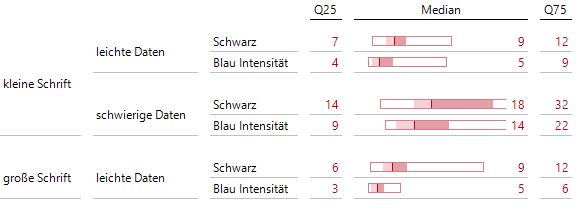
Diese Boxplots mit Quartilen und Median zeigen: Der Einsatz von Farbintensität senkt die Zeit.
Die Boxplots zeigen, dass erstens – wie zu erwarten war – schwierigere Daten zu höheren Zeiten führen. Klar sichtbar ist auch der Vorteil einer Schrift mit variierender Farbintensität, die zu verkürzten Suchzeiten führt.
Weiterhin ist noch ein Effekt der größeren Schrift zu sehen, der wohl zu einer besseren Wahrnehmung der unterschiedlichen Farbintensitäten führt. Hier muss man aber aufpassen, da während der Versuche ein Lerneffekt zu beobachten war. D. h. im dritten Block traten tendenziell bereits weniger Fehler auf als im ersten. Die zwei Zeilen der Intensität lassen sich aber gut vergleichen, da die Werte ja im gleichen Block, d. h. zur gleichen Zeit generiert wurden.
Aber wie sieht es nun mit den Zahlogrammen im Vergleich aus?
Schauen wir beispielsweise auf den Anteil der Fälle, bei denen die drei korrekten Zahlen auf Anhieb im ersten Versuch angeklickt wurden:
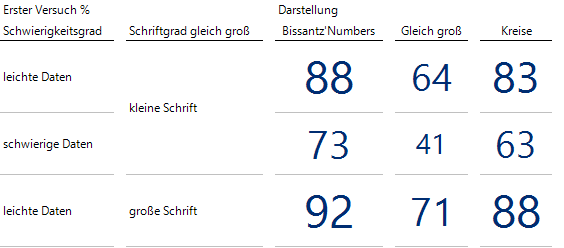
Anteil der Versuche in Prozent, die auf Anhieb korrekt gelöst wurden: höchster Wert für Zahlogramme!
Bei Bissantz’Numbers werden im Vergleich zu Kreisen häufiger die richtigen Zahlen auf Anhieb erkannt. Zwar reicht die Anzahl der Personen nicht aus, um von einem gesicherten Effekt gegenüber den Kreisen zu sprechen, aber die Tendenz stimmt.
Besonders schön dabei ist, dass die benötigte Zeit im Mittel bei diesen erfolgreichen Versuchen auch noch geringer ist:

Durchschnittlich benötigte Zeit bei den auf Anhieb erfolgreichen Versuchen: niedrigster Wert bei Bissantz’Numbers!
In diesen Darstellungen ist der Lerneffekt zwischen erstem und drittem Block sichtbar – sowohl für Bissantz’Numbers, als auch für Kreise – da der veränderte Schriftgrad nur die Darstellung “Gleich groß” betrifft. Die Anteile erhöhen sich, die Zeiten werden kürzer.
Bislang wurden alle Messungen aller Kandidaten der einfacheren Darstellung wegen aggregiert und somit wurde noch gar nicht auf individuelle Effekte eingegangen.
Beispielsweise variieren selbst die aus sechs Messungen gewonnenen mittleren Zeiten einer Person bei den schwierigen Daten bei Bissantz’Numbers von 4.9 bis 15.2 Sekunden, d. h. unsere Menge an Versuchspersonen ist sehr heterogen und kommt unterschiedlich gut mit einer Darstellungsform zurecht (keine Angst, wir nennen keine Namen!).
Entscheidend ist nun eher der komparative Vorteil: Wenn eine Person im Schnitt mit Zahlogrammen 15 Sekunden benötigt, aber mit Kreisen 20 Sekunden, sind Bissantz’Numbers relativ gesehen vorteilhaft.
Wir betrachten deshalb nun einzelne Personen und schauen, wie diese mit den drei Darstellungsformen zurechtkommen. In einem Durchgang hat eine Person 18 Aufgaben zu bewältigen, jeweils 6 zu jeder Darstellungsform. Da sich im Versuchsaufbau die Darstellungsformen zyklisch abwechseln, sollte es keinen Vorteil einer konkreten Darstellungsform aufgrund von Lerneffekten geben.
Nun sortieren wir die 18 Zeiten einer Person in einem Durchgang aufsteigend und schauen, an welchen Rängen eine ausgewählte Darstellungsform steht. Der optimale Fall wäre, wenn die Ränge 1 bis 6 belegt werden, der schlechteste Fall tritt auf, wenn die Ränge 13 bis 18 lauten. Wir nehmen die Summe der Ränge als Kriterium und normieren diese so, dass der beste Fall durch eine 0 und der schlechteste Fall durch eine 1 wiedergegeben wird.
Für jede Person ergibt sich nun pro Durchgang ein Tripel (B’N, GG, Kr). Beispielsweise besagt ein Tripel (0.26, 0.96, 0.28), dass die Person mit Bissantz’Numbers und Kreisen etwa gleich gut zurechtgekommen ist, aber mit “Gleich groß” einige Schwierigkeiten hatte. Die Summe der drei Tripelwerte ist übrigens immer exakt 3/2.
Insgesamt ergaben sich 55 Tripel. Der Wert von “Gleich groß” war für jede Person und jeden Durchgang höher als der entsprechende Wert der Bissantz’Numbers – wir konzentrieren uns deshalb auf den Vergleich Bissantz’Numbers gegen Kreise.
Werfen wir einen Blick auf die Portfolio-Analyse, die die Bissantz’Numbers-Werte den Kreiswerten gegenüberstellt:
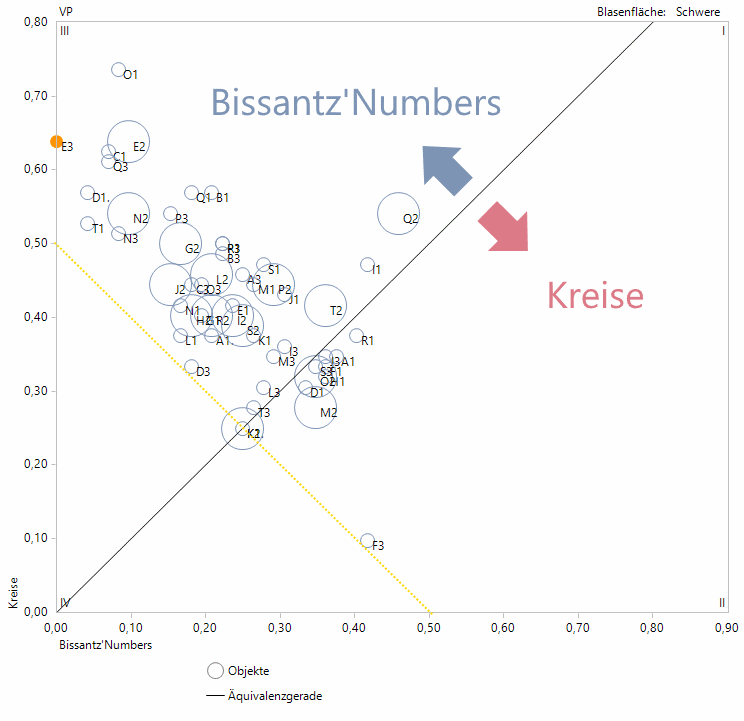
Viele Teilnehmer profitieren von den Bissantz’Numbers
Die Buchstaben A-T geben verklausuliert die 20 teilnehmenden Mitarbeiter wieder, die Ziffer steht für den Durchgang. Große Kreise kennzeichnen die schwere Datenkonstellation aus Durchgang 2.
Je besser jemand mit den Bissantz’Numbers klarkommt, desto weiter links ist seine Markierung angesiedelt. Je mehr Probleme er vergleichsweise mit Kreisen hat, desto weiter oben liegt die Markierung. Teilnehmer E hat im Durchgang 3 die sechs besten Ergebnisse durchgehend mit den Bissantz’Numbers erzielt und landet deshalb sogar auf der Ordinate. Bei Durchgängen nahe diesem Wert haben die Bissantz’Numbers geglänzt: niedrige Ränge für Zahlogramme, hohe Werte für Kreise.
Punkte oberhalb der eingezeichneten schwarzen Diagonalen (Grafikoption Äquivalenzgerade!) kennzeichnen somit Personen, die in einem Durchgang die besten Ergebnisse mit den Bissantz’Numbers erzielten, die Punkte unterhalb der Diagonalen kamen besser mit den Kreisen zurecht. Je weiter eine Markierung von der Diagonalen entfernt ist, desto eindeutiger ist der Vorteil der entsprechenden Darstellungsform.
Unterhalb der gepunkteten Linie in Orange (per Grafikprogramm eingefügt!) kann kein Tripel liegen: Ist der Bissantz-Wert 0, muss der Kreis-Wert mindestens 0.5 betragen und umgekehrt.
Ein einsamer Reiter (F3) war zumindest in einem Durchgang sehr von den Kreisen angetan.
Ohne Berücksichtigung der Größe des Effekts waren 43-mal die Bissantz’Numbers im Vorteil, 10-mal die Kreise und 2-mal herrschte Gleichstand. Im direkten Vergleich mit den Kreisen erzielen die Bissantz’Numbers einen mehr als deutlichen Punktsieg!
Mit diesem Experiment wurde ein wichtiger Teilaspekt untersucht: Wie schnell finde ich die relevanten Informationen der Tabelle?
Da das Experiment bei den Kolleginnen und Kollegen gut ankam, sind erweiterte Szenarios in naher Zukunft gut denkbar. Beispielsweise könnte geprüft werden, wie gut die Inhalte auch verinnerlicht werden, nachdem sie gefunden werden. Wir haben mit der Konzeption von passenden Testsituationen begonnen.
Auf unserer Landingpage können Sie sich übrigens umfassend zum Thema informieren, sich von Beispielen für eigene Anwendungen inspirieren lassen, Demo-Videos anschauen und auch ein kostenloses Excel-Add-In zum Selbstausprobieren herunterladen.