Ein häufig auftretendes Problem besteht darin, aus einer Menge von möglichen geographischen Orten den optimalen bezüglich des eigenen Standpunkts auszuwählen. Wir betrachten eine mögliche Strategie und ihre Darstellung in der Geo-Analyse von DeltaMaster.
In unserem Blogbeitrag Das Tool der Wahl aus dem Oktober 2017 hatten wir uns im Rahmen der Geo-Analyse unter anderem mit der automatisierten Generierung einer Markerposition innerhalb einer gegebenen Polygonfläche beschäftigt.
Es gibt ein Szenario, bei dem ein duales Problem gelöst werden muss: Gegeben sind nun die Marker und wir hätten gern jedem Marker eine Polygonfläche zugeordnet.
Bei der folgenden Problemstellung ergibt sich ein solches Polygon auf natürliche Weise: Gegeben sind feste Ortspositionen von Markern und wir möchten einer x-beliebigen (bzw. xy-beliebigen!), frei zu setzenden Ortskoordinate (x,y) die nächstgelegene Markerposition zuweisen:
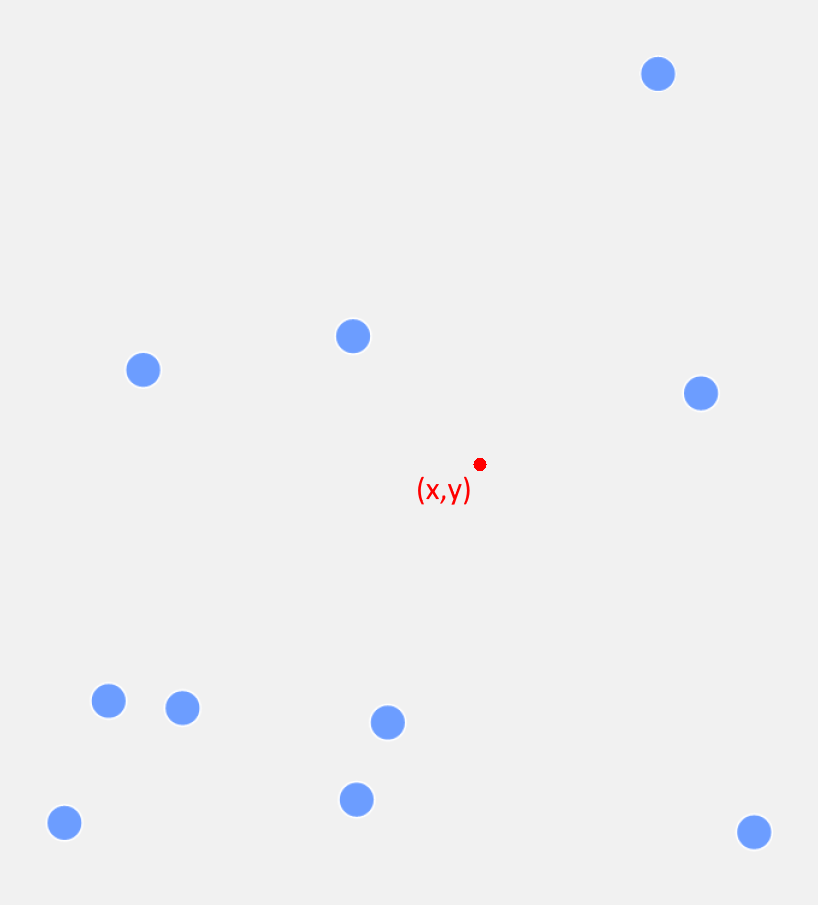
Welcher Marker (blau) liegt am dichtesten am Standpunkt (rot)?
Markerpositionen könnten etwa für Krankenhäuser, Supermärkte, Postkästen oder Wahllokale vorliegen. In diesem Falle muss man sich von der freien Ortskoordinate zu einer Markerposition bewegen.
Wir können uns aber auch leicht Beispiele vorstellen, bei denen die Bewegungsrichtung umgedreht ist. Feuerwehr- oder Notfalleinsätze kommen hier in den Sinn. Da hier aber für kürzere Distanzen auch noch das Straßennetz eine entscheidende Rolle spielt, wir aber eher die direkte räumliche Entfernung betonen möchten, seien in unserem Beispiel Standorte für Paketdrohnen gegeben, die in eher kleinstädtisch geprägten Räumen ohne störende Bauwerke oder Hindernisse eingesetzt werden sollen.
Natürlich ist Entfernung nur eine von mehreren relevanten Größen, andere wie etwa vorhandene Kapazitäten kommen ebenfalls in den Sinn.
Sicherlich möchte man das Problem, den nächsten Marker zu finden, möglichst allgemein lösen. Es existiert der Voronoi-Algorithmus, der die gesuchten Polygone generiert und jedem Marker den Bereich zuordnet, der von genau diesem Marker aus am schnellsten zu erreichen ist.
Manche Polygone erstrecken sich prinzipiell ins Unendliche; diese Polygone werden beispielsweise wie hier durch ein beschränkendes Rechteck (“bounding box”) gekappt, das so bemessen ist, dass alle relevanten frei definierbaren Ortspositionen auf jeden Fall enthalten sind.
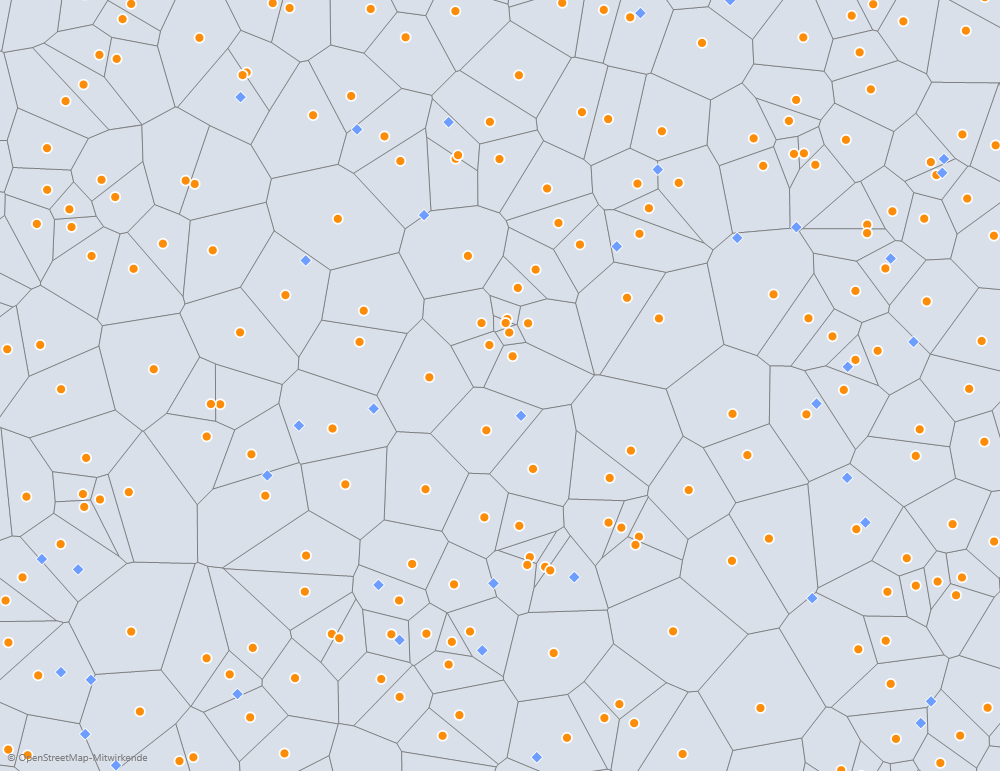
Wir haben ein Shapefile aus den Polygonen generiert, in DeltaMaster als Karte angebunden und das mit ein paar kommentierenden Elementen aus dem Grafikprogramm angereicherte Ergebnis sieht dann folgendermaßen aus:
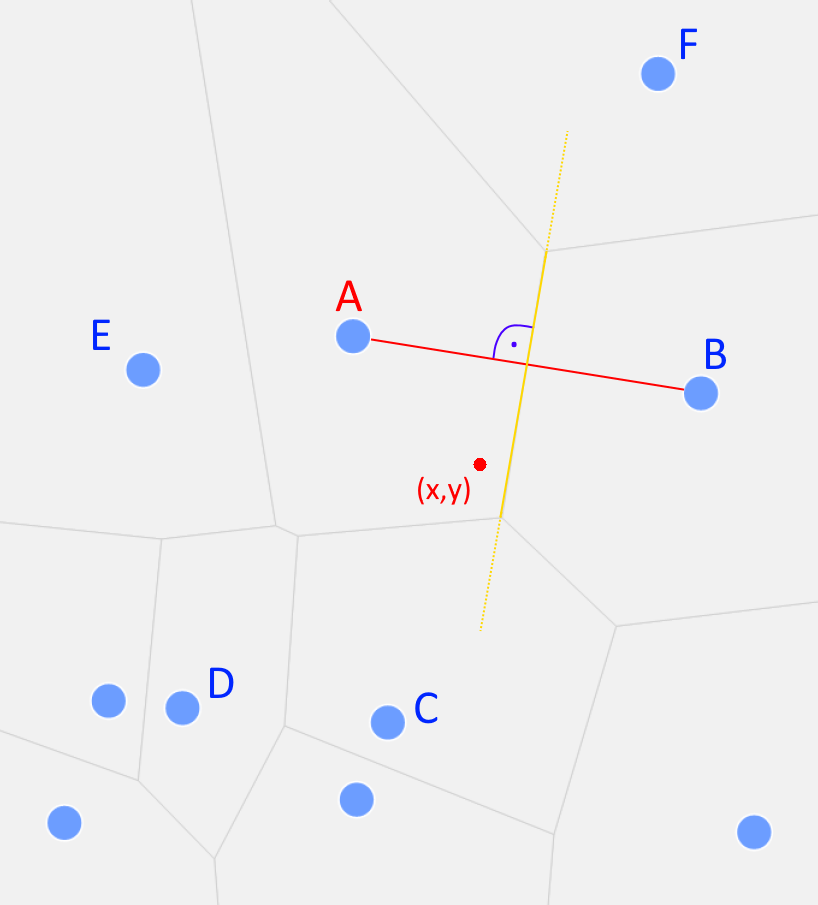
Das Voronoi-Diagramm des Beispiels
Die Drohne sollte also von A starten, da unser Standort (x,y) innerhalb des zugeordneten Polygons von A liegt.
Wodurch zeichnen sich die erzeugten Polygone aus? Ob etwa A oder B angeflogen wird, entscheidet sich aufgrund folgender Überlegungen:
Wir verbinden A und B auf direktem Wege (rote Strecke in obigem Diagramm) und errichten die Mittelsenkrechte (gelbe Linie). Alle Punkte links der gelben Linie liegen nun dichter an A, alle rechts der gelben Linie dichter an B). Analog gibt es für A relevante Grenzen mit C, D, E und F und die direkten Verbindungen mit A stehen immer senkrecht auf der zu einer trennenden Kante gehörenden Geraden.
Übrigens lassen sich die relevanten Nachbarn mit gemeinsamer Grenze aus dem Graphen der Delaunay-Triangulation ablesen:
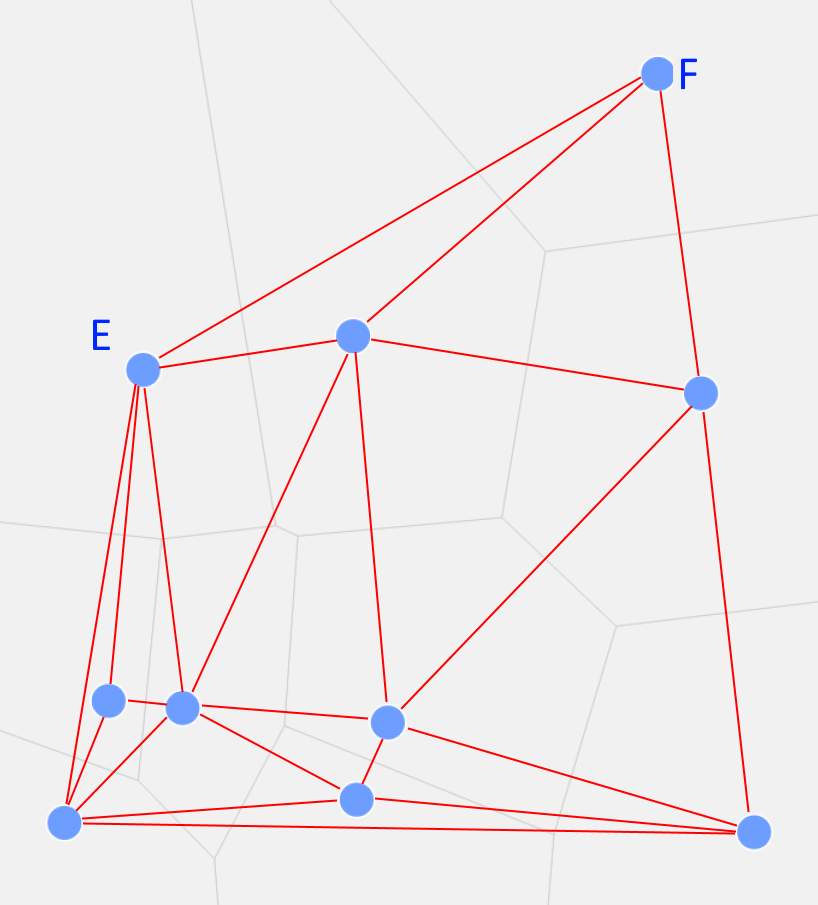
Die Delaunay-Triangulation des Beispiels
Sind in diesem Graphen zwei Marker verbunden, so besitzen sie eine gemeinsame relevante Grenze. Diese Grenze muss aber nicht zwingend von der zugehörigen roten Linie getroffen werden, sondern kann auch versetzt oder sogar außerhalb des Rechtecks – wie im Falle von E und F – liegen.
Wie sieht es aber aus, wenn wir größere Flächen abdecken, beispielsweise auf einer Welt- oder Europakarte? Die gekrümmte Erdoberfläche kann bekanntermaßen nicht verzerrungsfrei in einer zweidimensionalen Karte wiedergegeben werden, wie Leonhard Euler bereits 1777 bewies (Kapitel 1 des Werkes “Drei Abhandlungen über Kartenprojection”, Ueber die Abbildung einer Kugelfläche in einer Ebene, §9, Zitat “Damit ist auch durch Rechnung abgeleitet, dass eine vollkommen genaue Abbildung der Kugel in einer Ebene nicht möglich ist.”).
Bisher haben wir eine Ebene mit einem euklidischen Abstand angenommen; kürzeste Verbindungen sind dann durch Geraden gegeben und eine Strecke mit einer gegebenen Länge sieht immer gleich lang aus, unabhängig davon, wo und in welcher Orientierung sie gezeichnet wird.
Bei den üblicherweise verwendeten Projektionen wird die Erde durch eine Kugel – oder in den meisten Fällen sogar durch ein Ellipsoid – angenähert. Die kürzeste Verbindung auf einer Kugeloberfläche ist durch einen Großkreis gegeben. Zur Berechnung der Länge der Geodäte (diese Kurve mit dem kürzesten Abstand heißt bei einer Kugel auch Orthodrome) sei hier ein Kreis mit Umfang 40.000 km angenommen.
Man stelle sich bei dem erwähnten Großkreis am besten den Äquator als einen auf der Kugeloberfläche frei beweglichen, aber immer anliegenden Ring vor, der wieder so auf der Erde fixiert wird, dass er zwei gegebene Punkte verbindet. Dabei muss notgedrungen der Ringmittelpunkt mit dem Erdmittelpunkt identisch sein, ansonsten würde der Ring von der Erde abheben.
Man kann eine parametrische Form finden, sodass die Punkte des Großkreises durchlaufen werden. Wir schauen nun auf die Darstellung in unserer Karte.
Im folgenden Beispiel verbinden wir Hamburg und Wien auf der gezoomten Weltkarte (bitte klicken Sie auf die Grafik für eine vergrößerte Darstellung!):
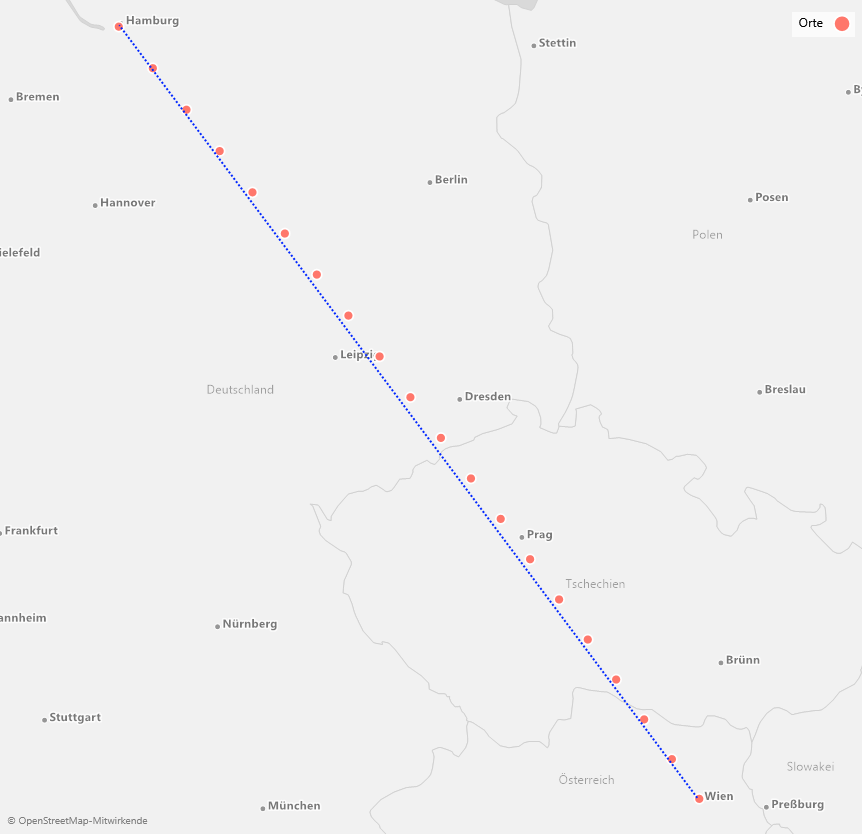
Kürzeste Verbindung auf der Karte (blau gestrichelt) und in Wirklichkeit (rote Marker)
Wien und Hamburg sind hier knapp 742 km voneinander entfernt. Die Grafik verdeutlicht, dass der kürzeste Weg über den Großkreis (rote Marker) in der Karte als gekrümmte Kurve erscheint, die aber noch relativ nahe an der direkten Verbindung auf der Karte verläuft. Vergrößern wir doch einmal die Entfernung und fliegen von Nürnberg nach Reykjavik:
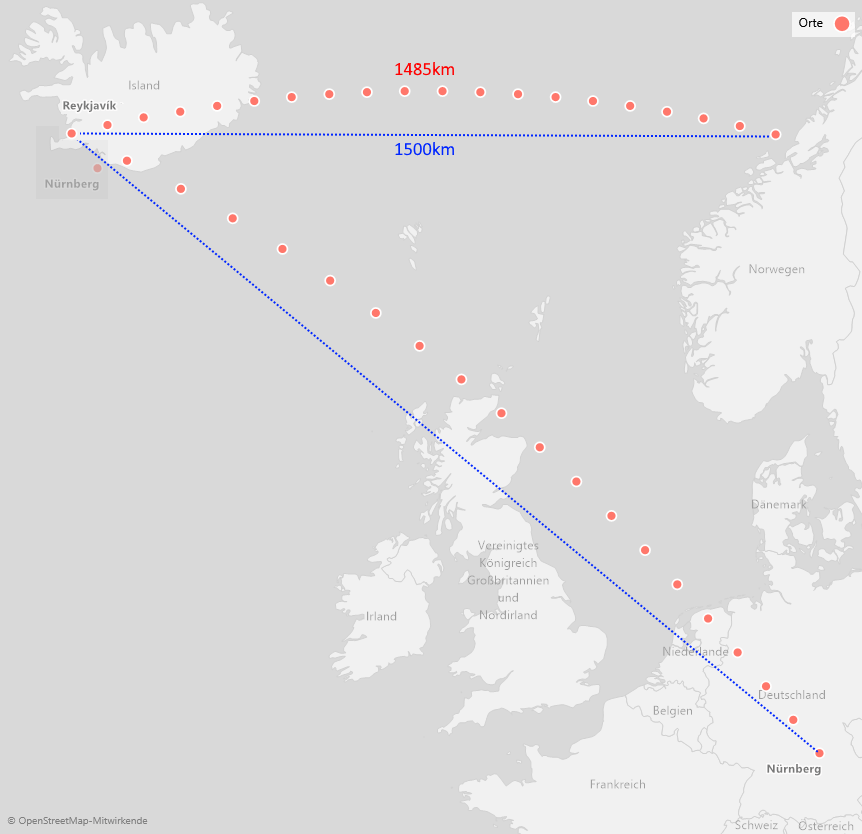
Von Nürnberg nach Reykjavik und dann 1500 km entlang des Breitengrades nach Osten
Hier wird der direkte Weg entlang der Orthodrome (rote Marker) auf der Karte durch einen stärker ausgeprägten Bogen dargestellt. Wir setzen den Flug fort und fliegen weiter, genau 1500 km entlang des Breitengrades in Richtung Osten. Alternativ hätten wir bei Verwendung der Geodäte 1485 km zurückgelegt und somit 15 km, also 1% des Weges einsparen können. Für die Navigation hingegen ist der etwas längere Weg leichter einzuhalten, da sogar ein einfacher Kompass ausreicht, um den Kurs nach Osten zu halten; für den kürzeren Weg hingegen ändert sich andauernd die einzuschlagende Himmelsrichtung und das Manövrieren ist bzw. war in früheren Zeiten deutlich schwieriger.
Die Marker von Nürnberg nach Reykjavik sind in gleichmäßigen Abständen über den Großkreis verteilt. In der obigen Grafik ist der erste Schritt vom Nürnberg-Marker bis zum nächsten Marker kopiert und transparent bei Reykjavik wieder so eingeblendet worden, dass der zweite Marker mit Reykjavik übereinstimmt. Es ist offensichtlich, dass auf der Karte die eigentlich gleich großen Abstände in der Nähe von Reykjavik größer dargestellt werden.
Werfen wir doch einen vertiefenden Blick auf das Verzerren von Abständen. Wie relevant ist die Verzerrung innerhalb Deutschlands (oder innerhalb Europas)? Bei Annahme einer Kugelgestalt bedeutet ein Unterschied von 1 Grad im Breitengrad bei gleicher Länge etwa eine Entfernung 40000 / 360 ~ 111,11 km. In der folgenden Abbildung bewegen wir uns entlang des Längengrades durch Nürnberg und tragen alle 55,556 km (dies entspricht einem halben Grad) einen Marker ein. Zusätzlich bewegen wir uns von jedem dieser Marker entlang des Breitengrades viermal jeweils 55,556 km nach Osten. Wie sieht das Ergebnis in der Karte aus?
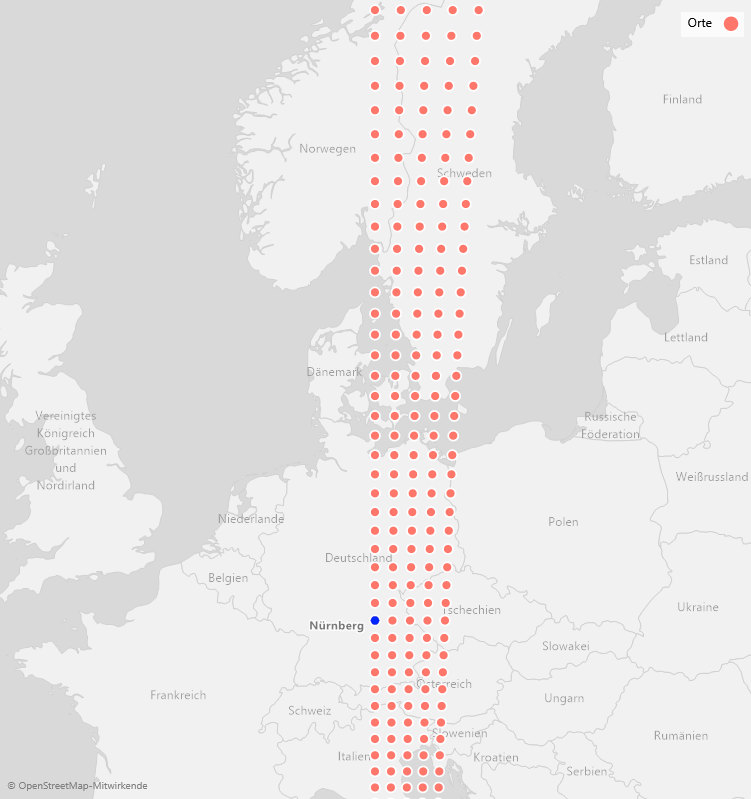
Immer 55,556 km von Gitterpunkt zum direkten Nachbarn!
Erstens stellt man fest, dass ein Meridian wie etwa der Längengrad durch Nürnberg immer senkrecht und alle Breitengrade stets waagerecht auf der Karte erscheinen.
Weiterhin ist ersichtlich, dass die rund 55,556 km von einem Marker zum direkten Nachbarn links oder rechts, bzw. alternativ unten oder oben, von Süd nach Nord auf der Karte immer größer dargestellt werden. Falls Sie bisher den Eindruck hatten, im Norden Deutschlands mit dem Auto deutlich schneller voranzukommen, liegt es nicht nur an der flachen Landschaft, sondern auch an der Projektion der Karte. 1 cm auf der Karte entsprechen im Norden einer knapp 20 % kürzeren tatsächlichen Strecke im Vergleich zum Süden!
Kürzeste Wege sind krumm und gleiche Abstände variieren auf der Karte und damit variieren auch gleich große Flächen. Ist das Erstellen des Voronoi-Diagramms hier somit ein hoffnungsloser Fall? Die Antwort ist, dass es davon abhängt, wie dicht die Marker gesät sind.
Bei spärlicher Verteilung von Markern sind die Unterschiede stärker ausgeprägt. In folgendem Beispiel ist der Großkreis in Blau eingezeichnet, dessen Punkte von Hamburg und Wien gleich weit entfernt sind.
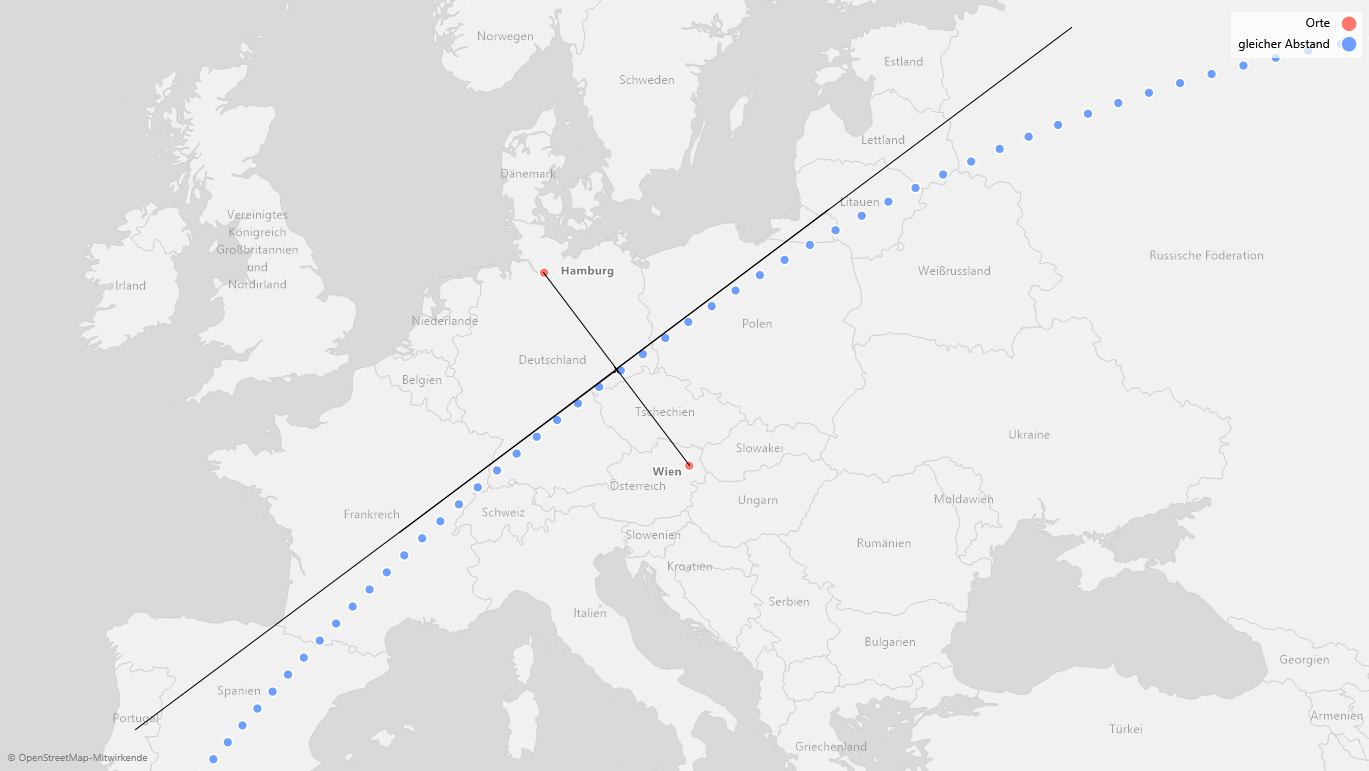
Blaue Punkte: Gleiche Abstände von Hamburg und Wien
Arbeitet man mit den sichtbaren Koordinaten nach der Projektion, also sozusagen auf dem Bildschirm, ist der Punkt auf direkter halber Strecke zwischen Wien und Hamburg (Kreuzung der schwarzen Linien) nur wenig von der wahren Mitte (der blaue Marker nebenan) entfernt. Je weiter man sich jedoch von der direkten Verbindung fortbewegt, desto größer werden die Fehler: Ein beträchtlicher Teil Spaniens und Portugals wird dichter an Wien gewähnt, obwohl eigentlich Hamburg näher gelegen ist. In der Karte schätzt man Lissabon, das ungefähr beim w von Mitwirkende im Copyright-Hinweis liegt, als etwas dichter an Wien (2300 km) gelegen ein, aber tatsächlich sind es im Vergleich nur 2200 km bis Hamburg.
Dass die Bildkoordinaten ein weiteres Manko haben, wird deutlich, wenn man sich etwa an die Ränder der Weltkarte bewegt. Von Alaska bis Kamtschatka muss man in Bildkoordinaten Nordamerika, den Atlantik und den eurasischen Kontinent überqueren, obwohl die wahre Entfernung auf der Erdkugel deutlich geringer ist und somit eine nicht genutzte Abkürzung aus dem linken Bildrand heraus zum rechten existiert.
Je kleiner der betrachtete Ausschnitt, desto weniger spielt die Erdkrümmung bei den verwendeten Projektionen eine Rolle. Zoomen wir in die Gittergrafik von eben hinein, ergibt sich das folgende Bild:
Man muss hier zweimal hingucken, um zu erkennen, dass die Gitterpunkte von unten nach oben auseinanderlaufen. Wenn also die Längenverzerrung vernachlässigbar ist, wird auch das aus den Bildschirmkoordinaten gewonnene Voronoi-Diagramm bei dichter Markerbelegung von den wahren trennenden Großkreisen wenig abweichen – die Krümmung kommt auf kurzen Distanzen noch nicht zum Tragen.
Es gibt noch einen kleinen Haken: Der Anwender besitzt normalerweise nur die Längen- und Breitenangaben und nicht die (Bildschirm-) Koordinaten nach der Projektion, wie sie von der verwendeten Komponente berechnet werden. Diese stehen normalerweise nur der Entwicklungs-Abteilung oder ausgebildeten Kartographen zur Verfügung.
Oft ist es trotzdem möglich, für Gebiete mit überschaubarer Ausdehnung direkt mit den Breiten- und Längengraden zu arbeiten, doch müssen die Werte der Längengrade vorübergehend gestaucht werden. Im Süden Deutschlands entspricht ein Unterschied von 1 Grad in der Länge einer Distanz von ca. 76 km und im Norden einer Distanz von 64 km, während ein Delta von 1 Grad im Breitengrad immer etwa 111 km ergibt. Im Süden wird der Stauchungsfaktor etwa 76/111 ~ 0.68 sein, im Norden beträgt er etwa 64/111 ~ 0.58.
Für die transformierten Punkte wird das Voronoi-Diagramm mit existierenden Algorithmen erstellt, die Ecken der generierten begrenzenden Polygone müssen allerdings dann wieder rücktransformiert, d. h. entlang der Breitengrade gestreckt werden. Die folgende Karte ist dann ein mögliches Ergebnis, das dann im Shapefile-Format in DeltaMaster angebunden werden kann:
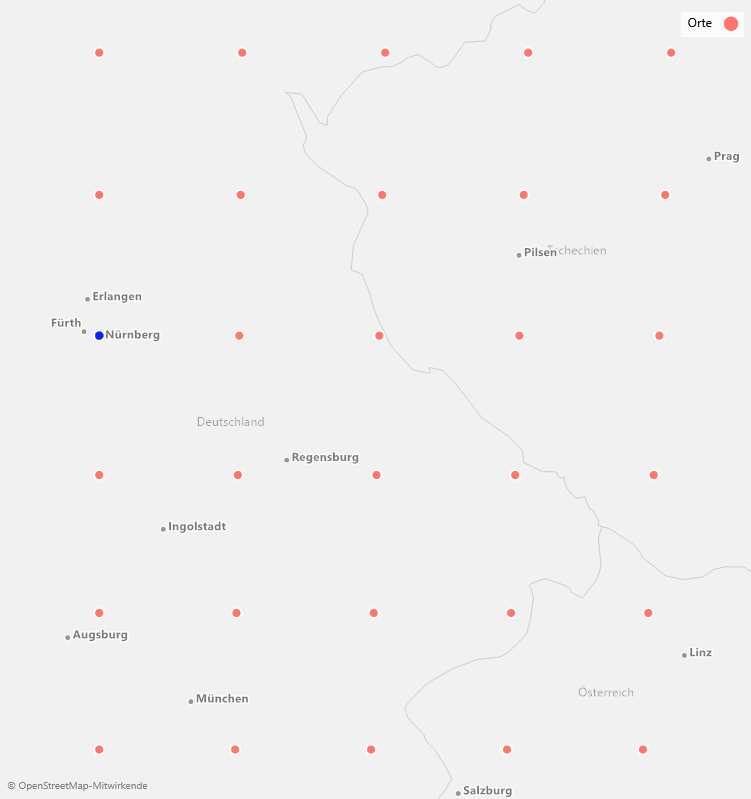
Hier bilden die orangefarbenen Marker die Grundlage für die Erzeugung des Voronoi-Diagramms. Es könnten beispielsweise Lager zur Auslieferung sein oder die bereits erwähnten Startplätze der Paketdrohnen. Gleichzeitig sind Kunden (blaue Marker) dargestellt, die beliefert werden müssen. Die Karte unterstützt somit das visuelle Verständnis zur Identifizierung des nächsten Lagers: In welchem Polygon sich ein Kunde befindet, kann mit einem Blick sehr leicht erfasst werden!
Es ist auch möglich, zusätzlich einen Kartendienst zu verwenden und durchscheinen zu lassen. Der obige Ausschnitt sieht dann folgendermaßen aus:
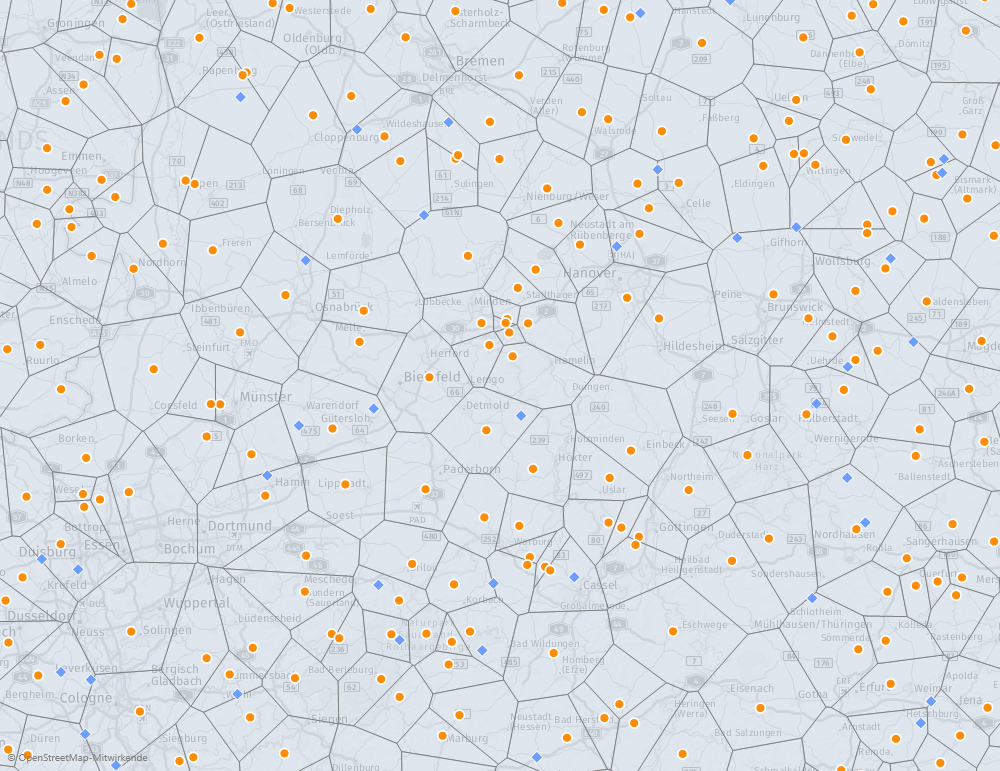
Voronoi-Diagramm mit Kartendienst
Obwohl das dargestellte Voronoi-Diagramm nur eine Näherung ist, wird es sich vom “wahren”, auf einem Ellipsoid abgeleiteten exakten Verfahren, das dann in der Projektion Bögen mit leichter Krümmung entstehen ließe, nur minimal unterscheiden. Für die Praxis reicht hier die Näherung vollkommen aus.