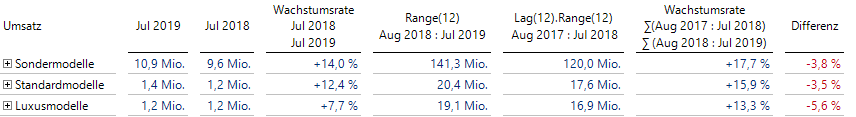In regelmäßig erstellten Berichten werden häufig aktuelle Kennzahlen – z. B. diejenigen eines betrachteten Monats – mit Werten der Vorperiode oder der Vorjahresperiode verglichen. In DeltaMaster sind – vor allem mit den Neuerungen des letzten Releases – auch in relationalen Anwendungen äußerst hilfreiche Konstruktionen mit Zeitanalyseelementen möglich, die einen spürbaren Mehrwert ergeben und den Selfservice-Anhängern gefallen werden.

Zeitanalyseelemente in relationalen Anwendungen

Grundsätzliches Vorgehen

In den letzten Releases, unter anderem auch in der neuesten Version 6.3.3 unserer Business-Intelligence-Software DeltaMaster, wurden die Möglichkeiten der Zeitanalyseelemente für relationale Anwendungen deutlich erweitert.

Die Logik der Zeitanalyseelemente ist eine relative: Etwa zu einem ausgewählten Monat möchte man weitere Kennzahlen sehen – zum Beispiel den Wert des Vormonats, den Vorjahreswert oder den kumulierten Wert im laufenden Quartal oder im gesamten aktuellen Jahr.

Während der MDX-Sprachumfang bei Verwendung von OLAP-Cubes für derartige Aufgaben sofort nutzbare Konstrukte wie zum Beispiel PeriodsToDate, ParallelPeriod, Cousin und viele weitere bereits vorhält, ist es bei rein relationalen Anwendungen schwieriger – aber nur für uns und nicht für Sie!

Das Definitionsfenster für Zeitanalyseelemente

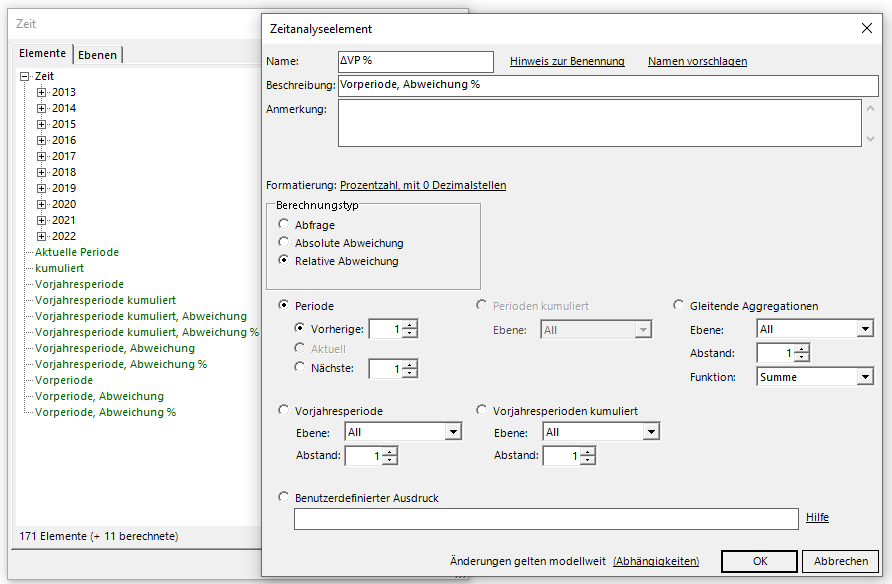
Wir gehen davon aus, dass wir eine hierarchische Zeitdimension mit Jahren, Quartalen und Monaten explizit modelliert haben, wie etwa in unserer Demo-Anwendung Chair, die wir hier verwenden möchten. In der Zeitdimension werden von DeltaMaster automatisch die am häufigsten verwendeten Zeitanalyseelemente angelegt (hier grün eingefärbt), deren Definition wir uns auch anschauen können.

In der obigen Abbildung (klicken Sie bitte auf die Grafik für eine vergrößerte Darstellung) blicken wir auf die relative Abweichung zum Vorjahreswert. Wollten wir ein solches Zeitanalyseelement selbst anlegen, müssten zwei Radio-Buttons zur Definition aktiviert werden – Berechnungstyp „Relative Abweichung“ und Periode „Vorherige“ mit eingestelltem Wert 1.

Sowohl absolute als auch relative Abweichungen beziehen sich immer auf die im Filter ausgewählte Periode (hier in unserem Datenbeispiel ist das immer ein Monat!).

Aggregationsfunktionen über Bereiche

Es ließen sich auch schon bisher gleitende Aggregationen anlegen, bei denen auf eine Reihe von Funktionen (Summe, Mittelwert, Minimum, Maximum, Standardabweichung, Varianz) zurückgegriffen werden kann:

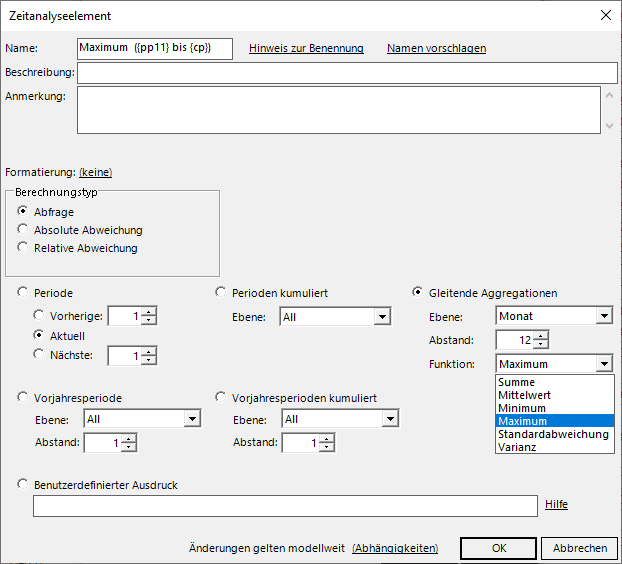
Gleitende Aggregationen: Maximum der letzten 12 Monate

Hier bestimmen wir zum Beispiel das Maximum der letzten 12 Monate. Diese Aggregationen laufen immer von einer Periode in der Vergangenheit bis zur aktuell gewählten Periode, die somit immer inkludiert ist. Wir erhalten dann in einem typischen Bericht ein Ergebnis wie das folgende:

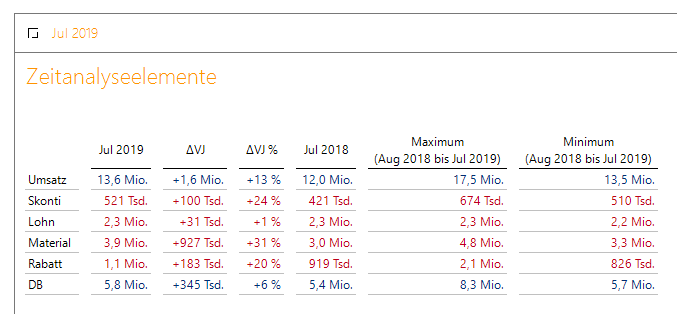
Gewählter Monat im Filter, Zeitanalyseelemente auf der Spaltenachse!

Im Filter wird der Monat ausgewählt, hier also Juli 2019. Auf der Spaltenachse wählen wir die gewünschten Zeitanalyseelemente aus – aktueller Wert, absolute und relative Abweichungen zum Vorjahreswert, der Vorjahreswert selbst und hier als Zusatz Maximum und Minimum der letzten 12 Monate. Im nächsten Monat wird im Filter August 2019 eingestellt und der Bericht aktualisiert sich von selbst.

Solchermaßen erstellte Berichte verlangen geradezu nach dem Publisher – hier kann der gewünschte Monat auch automatisiert aus dem jeweiligen Rechnerdatum gewonnen werden. Dann ist für diesen Bericht keinerlei händische Anpassung mehr notwendig.

Neuerungen in den Releases 6.3.1.1 und 6.3.3

Benutzerdefinierter Ausdruck: Referenzierte Elemente

Mit den neuesten Releases von DeltaMaster lässt sich ein benutzerdefinierter Ausdruck anlegen, den wir am unteren Ende des Definitionsfensters für Zeitanalyseelemente finden:

Benutzerdefinierter Ausdruck

Dieser Punkt wirkt sehr unscheinbar, aber eigentlich sollte hier zum Ausdruck der neu geschaffenen Möglichkeiten ständig eine Animation mit Feuerwerk und Konfettiregen ablaufen. Wir können sehr flexibel auf einzelne Elemente, aber auch auf bestimmte Mengen von Elementen in der Zeithierarchie zugreifen.

Fangen wir mit den referenzierbaren Elementen in der Zeithierarchie an. Zur Erinnerung zeigen wir hier noch einmal den Aufbau in unserem Modell:

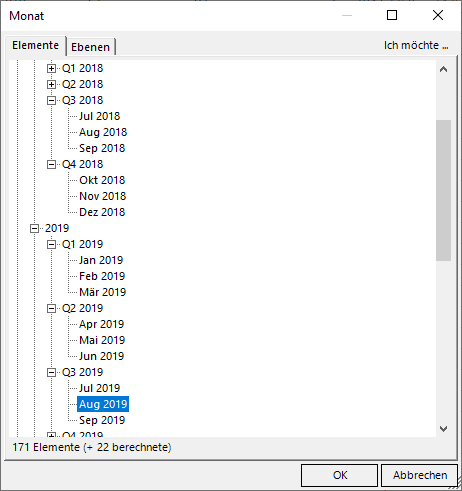
Zeithierarchie mit Jahr, Quartal und Monat

Möchte man einfach die aktuell gewählte Periode referenzieren, so geschieht dies mit dem Ausdruck „Current“. Auf der gleichen Ebene bewegt man sich mit lag(x) x Schritte in die Vergangenheit und mit lead(x) x Schritte in die Zukunft. Ist x = 1, kann ersatzweise previous bzw. next verwendet werden. Zwischen Groß- und Kleinschreibung wird übrigens nicht unterschieden.

Außerdem kann in der Hierarchie nach oben navigiert werden, entweder durch direkte Angabe des Levels (hier wären zum Beispiel noch Year oder Quarter oberhalb der Monatsebene möglich) oder auf relativem Wege über „Parent“.

Es gibt häufig mehrere Wege, um ein konkretes Element relativ zum Ausgangsmonat anzusteuern. Für die komplette Referenz verweisen wir auf die Hilfe.

Die bisherigen Befehle können nun auch kombiniert werden!

Sei nun im Filter beispielsweise der August 2019 eingestellt. Verwenden wir etwa den Ausdruck „Current.Parent.Lag(1)“, wird dieser von links nach rechts aufgelöst.

Wir haben einmal jeweils ein Zeitanalyseelement zu jedem Zwischenschritt angelegt und die Folge der Zeitanalyseelemente in der folgenden Grafischen Tabelle dargestellt. Die Zeitanalyseelemente der Zwischenschritte müssen natürlich nicht zwingend vorhanden sein und dienen hier nur der Illustration.

Dass in den Namen in der jeweils ersten Zeile auch die Definition sichtbar ist, soll hier nur einfacher vermitteln, welcher Befehl verwendet wurde. Im täglichen Einsatz verzichten wir natürlich normalerweise auf diese Angabe!

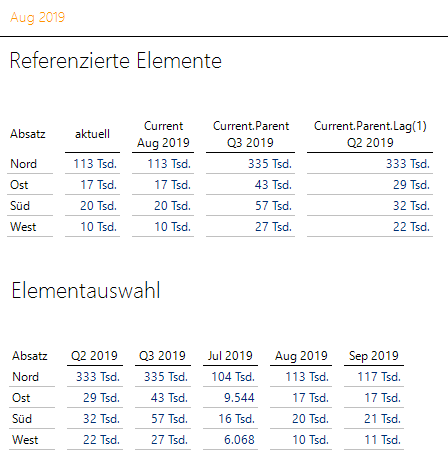
Zeitanalyseelemente können über Verkettung erstellt werden

Für Zweifler wurde unten eine Grafische Tabelle gegenübergestellt, in der wir die gewünschten Monate und Quartale per Elementauswahl direkt und somit statisch aus der Zeitdimension ausgewählt haben.

Current.Parent.Lag(1) könnte somit, falls im Filter mit August 2019 der aktuell laufende Monat angegeben ist, das letzte komplett vorliegende Quartal „Q2 2019“ bezeichnen.
Ein Current am Beginn eines Ausdrucks kann übrigens auch weggelassen werden.

Benutzerdefinierter Ausdruck: Referenzierte Mengen und Aggregationsfunktionen

Bereiche mit flexibler Länge

Mit der im letzten Abschnitt vorgestellten Technik kann man von einer gegebenen Periode aus jede andere Periode erreichen, die auf der gleichen oder höheren Ebene liegt wie die im Filter eingestellte Periode; diese kann auch in der Zukunft liegen.

Ausgehend von diesem Referenzelement (dieses kann auch das unveränderte „Current“ sein), das auch bereits für sich hilfreiche Information liefert, können nun Bereiche bzw. Mengen definiert werden, die vom Referenzelement aus in die Vergangenheit reichen. Auf die Mengen wiederum kann dann eine Aggregatsfunktion aus dem Pool (Summe, Mittelwert, Minimum, Maximum, Standardabweichung, Varianz) angewendet werden. Die zu verwendenden Kürzel lauten dabei Sum, Avg, Min, Max, StdDev und Var.

Zunächst gibt es die Mengenbefehle, die meist der Ermittlung kumulierter Werte dienen; häufig wird als Anfang der Jahresbeginn gewählt. Befindet man sich zum Beispiel mitten im August 2019 und möchte den aggregierten Wert aller abgeschlossenen Monate dieses Jahres ermitteln, so lautet ein möglicher Befehl „Current.Lag(1).YearToDate“ oder vereinfacht „Lag(1).YearToDate“, da das „Current“ gegebenenfalls am Anfang automatisch hinzugefügt wird.

Möchte man die kumulierten Werte nur in diesem Quartal sehen, inklusive des aktuellen Monats, so kann man „QuarterToDate“ oder auch kürzer „QtD“ nehmen:

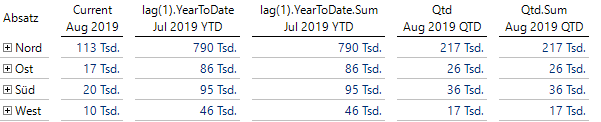
Kumulierte Werte im Jahr oder im Quartal

Solange man keine Aggregatsfunktion angibt, wird diese aus dem Aggregationstyp der jeweiligen Kennzahl abgeleitet. Bei Absatz ist dieser normalerweise durch die Summe gegeben, sodass sich die Ergebnisse hier nicht verändern, wenn explizit noch ein „Sum“ angefügt wird. Der Vorteil, auf den Aggregationstyp verzichten zu können, wird dann sichtbar, wenn mehrere Kennzahlen mit unterschiedlichem Aggregationsstyp vorliegen. Hier reicht dann ein einziges Zeitanalyseelement aus, das sich an das gewünschte Aggregationsverhalten der Kennzahl anpasst.

Es gibt in unserer Hilfe Empfehlungen, wie der Anwender den Namen eines solchen Elementes mittels DeltaMaster-Variablen aufbauen sollte. Im Falle der ersten Aggregation seit Jahresbeginn bis zum abgeschlossenen Vormonat steht hier (in der zweiten Zeile verwendet!) beispielsweise „{pp1} YTD“ und im anderen Fall des Quartals „{cp} QTD“.

Range: Bereiche mit fester Länge

Besonders geeignet für rollierende Summen oder Mittelwerte ist der Range-Befehl. In der einfachen Variante setzt man die Anzahl der Perioden ein, die inklusive des Referenzelements in Richtung Vergangenheit verwendet werden soll.

Ist August 2019 im Filter, so berechnet „Range(12).Avg“ zum Beispiel den Mittelwert der Monate September 2018 bis August 2019 und „Lag(1).Range(12).Avg“ den Mittelwert der Monate August 2018 bis Juli 2019.

Mit dem neuesten Release 6.3.3 von DeltaMaster gibt es hier eine Erweiterung mit einem zweiten Parameter „Abstand“, sodass die ausgewählten Elemente nicht zwingend aufeinanderfolgen müssen, sondern einen beliebigen festen Abstand haben können. Ist wie bisher August 2019 im Filter, so ergibt „range(3,12).avg“ den Mittelwert der 3 Monate August 2017, August 2018 und August 2019.

Wie und wo solche und bisher noch nicht erwähnte weitere Konstruktionen eingesetzt werden können, zeigen wir nun direkt im folgenden Abschnitt der Beispielanwendungen.

Beispielanwendungen

Rollierende Wachstumsrate

Fangen wir mit einem Beispiel an, das sich nun sehr einfach mit dem neuesten Release umsetzen lässt. Wir möchten gerne die Umsätze der letzten 12 Monate mit den 12 Monaten zuvor vergleichen und eine Wachstumsrate ausrechnen.

Mit dem neuesten Release lässt sich nun auch aus Zeitanalyseelementen ein neues berechnetes Element zusammensetzen, das ebenfalls auf der Spaltenachse verwendet werden kann. Deshalb brauchen wir nur zwei Zeitanalyseelemente „Range(12)“ und „Lag(12).Range(12)“ zu definieren und dann ein berechnetes Element, das eine relative Abweichung dieser beiden Elemente enthält. Die erste Summe könnte alternativ auch als „Gleitende Aggregation“ definiert werden, da sie mit dem aktuell gewählten Monat endet:

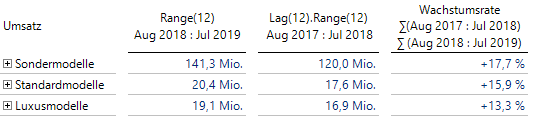
Wachstumsrate auf rollierenden 12-Monats-Zeiträumen

Wir spinnen dieses Beispiel weiter und vergleichen diese Wachstumsrate mit der Wachstumsrate nur für den gewählten Monat im Vergleich zum Vorjahresmonat.

Außerdem legen wir noch ein berechnetes Element mit der Differenz der beiden Wachstumsraten an:

Einfache Wachstumsrate im Vergleich zur rollierenden Wachstumsrate

Nun sehen wir, dass die 14.0 % Zuwachs für Sondermodelle im Juli 2019 zwar recht hoch aussehen, aber im Jahresvergleich der Zuwachs mit 17.7 % noch höher ausfiel.

Wir verbinden den Umsatz mit dem Zeitanalyseelement Differenz zu einem Filterwert gleichen Namens und können diesen z. B. in PowerSearch nutzen, um Regionen/Produktgruppen-Kombinationen zu finden, bei denen die Wachstumsrate im aktuellen Monat besonders stark von der rollierenden 12-Monats-Wachstumsrate abweicht:

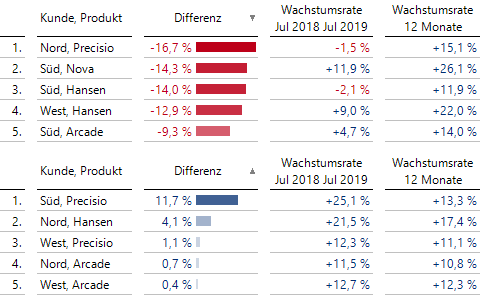
Auffällige Wachstumsraten des Monats, relativ gesehen zur rollierenden Wachstumsrate

Nord/Precisio fällt in diesem Monat besonders negativ, Süd/Precisio besonders positiv auf!

Performance-Maß eines Monats im Vergleich zu Vorjahres-Monaten

Die Annahme ist, dass wir den Absatz eines ausgewählten Monats nur mit den gleichen Monaten vorangegangener Jahre vergleichen wollen. Als Maß wählen wir das Verhältnis des aktuellen Monats zum Maximum der Vergleichswerte.

Mit „Range(3,12).Max“ erhalten wir das Maximum der letzten drei Jahre für den ausgewählten Monat – inklusive des aktuellen Monats.

Nun wird ein Quotient aus dem aktuellen Wert und dem Maximum der letzten drei Jahre (nur für den gewählten Monat, aktueller Wert inklusive) berechnet:

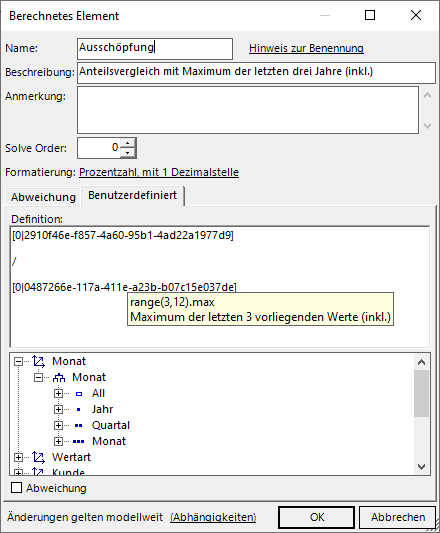
Berechnetes Element als Quotient aus Aktuell und dem Maximum

Die etwas kryptischen Bezeichnungen werden durch die verständliche Beschreibung ersetzt, wenn man mit gedrückter Alt-Taste mit der Maus über den Text fährt.

Übrigens muss man bei den Berechnungen speziell bei benutzerdefinierten Quotienten etwas aufpassen, da der neue zugewiesene Typ implizit von der Datenbank (und unterschiedliche Datenbanken verhalten sich nicht zwingend gleich!) aus den Typen der beteiligten Variablen abgeleitet wird. Sollten in der Datenbank Nenner und Zähler als Integer definiert sein z. B. 3 / 5, dann darf man sich nicht wundern, wenn das Ergebnis auf einmal 0 und nicht 0.6 heißt. Um auf der sicheren Seite zu sein, könnten Sie eine Variable x immer als Cast(x as float) verwenden.

Nun lässt sich die folgende Grafische Tabelle erstellen:

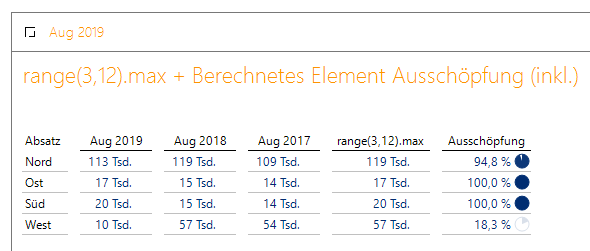
Vergleich aktueller Monat zu den letzten drei Werten

Hier sieht man nun, dass in Ost und Süd in diesem Jahr der maximale Absatz erzielt wurde, in West hingegen geschwächelt wird: Hier werden nur magere 18.3 % eines bereits erzielten Absatzes von August 2018 erreicht.

Ein kleiner Wermutstropfen muss an dieser Stelle erwähnt werden. Die Möglichkeit, berechnete Elemente in der Zeitdimension anzulegen, gibt es nur, wenn die Zeithierarchie explizit mit allen Ebenen modelliert wurde, aber (noch) nicht, falls eine virtuelle Zeitdimension verwendet wird.

Alternativ lässt sich auch eine relative Abweichung zum Maximum der letzten 3 identischen Monate ohne den aktuellen Monat berechnen. Dazu legen wir ein Zeitanalyseelement „Lag(12).Range(3,12).Max“ an.

Diese Verkettung bedeutet, dass wir vom aktuellen Monat (hier nehmen wir einmal März 2020) startend 12 Monate zurückgehen (also zu März 2019) und dieses Referenzelement und seine beiden Vorgänger im Abstand von jeweils 12 Monaten (also letztendlich März 2019, März 2018 und März 2017) betrachten. Schließlich berechnen wir auf diesen drei Elementen das Maximum.

Dann können wir ein berechnetes Element mit einer relativen Abweichung des aktuellen Wertes zum Maximum definieren:

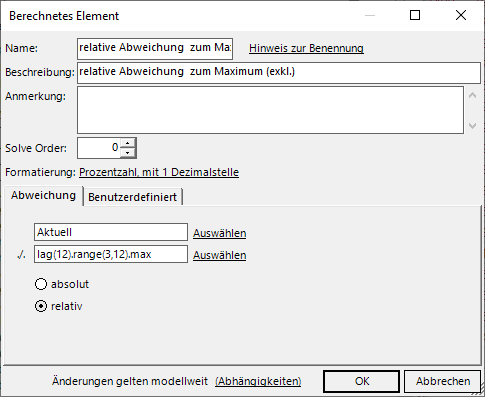
Berechnetes Element mit relativer Abweichung des aktuellen Monats zum Maximum der vorhergehenden drei Werte

In der folgenden Grafischen Tabelle sehen wir den aktuellen Wert und seine drei Vorgänger, das Maximum der drei Vorgänger und die relative Abweichung des aktuellen Wertes zum Maximum:

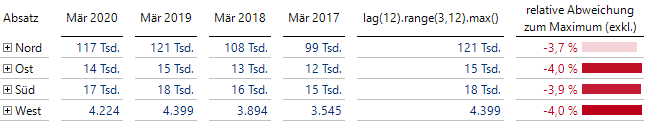
Vergleich aktueller Monat mit Maximum der vorhergehenden drei Werte

Hier gab es also für jede Region in der Vergangenheit leicht höhere Absatzwerte im März. Die Maxima kommen immer aus dem Vorjahr 2019.

Lineare Regression mit Prognose

Daten ohne Saisonkomponente

Es gibt mit LinRegSlope einen interessanten Befehl, mit dem man in einem benutzerdefinierten Ausdruck eine einfache lineare Regression nachbilden kann. Mit „Range(13).LinRegSlope“ wird etwa die Steigung der Regressionsgeraden auf den letzten 13 Werten der Kennzahl inklusive des aktuellen Wertes berechnet.

Steigung der Regressionsgeraden mit LinRegSlope ermitteln

Bei Zeitreihen ohne Saisonkomponenten lassen sich die auch aus unserem Trendbarometer bekannten durchschnittlichen Änderungen in einem eigens erstellten Zeitanalyseelement nutzbar machen.

Mit dessen Hilfe lassen sich dann auch Prognosen erstellen.

Im Regressionsmodell sind die y-Werte durch die Kennzahl gegeben. Bei den x-Werten haben wir aber noch einen Freiheitsgrad in der Längsrichtung. Wir könnten die x-Werte 0 bis 12 nennen oder aber auch 1 bis 13 oder 7 bis 19.

Besonders einfach werden aber die Schätzer der Steigung und des Achsenabschnitts der Regressionsgeraden, wenn wir eine um 0 symmetrische Darstellung wählen, also hier x = -6, -5, …, 0, …, 5, 6 verwenden. Es lässt sich dann zeigen, dass der geschätzte Achsenabschnitt b der Regressionsgeraden y = ax + b dem Mittelwert der Beobachtungen entspricht, den wir aber auch einfach mit „Range(13).Avg“ berechnen können. Eine 1-Schritt-Prognose in die Zukunft ist dann zum Beispiel an der Stelle x = 7 zu finden.

Wir legen ein berechnetes Element an, das zum Mittelwert das 7-fache der Steigung addiert, und schon können wir unsere Vorschauwerte auch selbst berechnen und weiterverwenden:

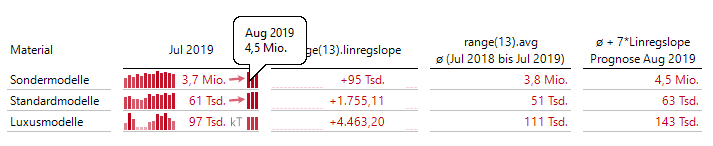
Vorschauwerte selbstgemacht

Für eine Prognose des übernächsten Monats müssten wir das 8-fache der Steigung addieren.

Daten mit Saisonkomponente

Liegen Zeitreihen mit Saisonkomponenten vor, ist die Nachbildung der Vorschauwerte immer noch relativ einfach möglich, wenn der betrachtete Zeitraum ein ganzzahliges Vielfaches (2, 3, …) der Periodenlänge ist. Man kann dann die Steigung der Regressionsgeraden immer noch in einer überschaubaren Formel ausdrücken und muss zum Mittelwert der passenden Perioden der vergangenen Jahre ein bestimmtes Vielfaches der Steigung addieren.

Hat man beispielweise Daten von Januar 2018 bis Dezember 2020, also von 36 Monaten, und steht dabei auch auf dem Monat Dezember 2020 und benötigt nun die Prognose für Januar 2021, so lauten die notwendigen Bestandteile, die als Zeitanalyseelemente definiert werden: „Lag(24).Range(12).Sum“, „Range(12).Sum“ und „Lag(11).Range(3,12).Avg“.

„Lag(24).Range(12).Sum“ entspricht den ersten 12 Monaten, hier bei Stand auf Dezember 2020 also dem Jahreswert 2018, „Range(12).Sum“ dem Jahreswert 2020 und die Differenz, geteilt durch 288 (= 12 * 24), ergibt die Steigung pro Monat. Der Mittelteil 2019 hat aus Symmetriegründen keinen Einfluss auf die Steigung, nur auf den Achsenabschnitt. „Lag(11).Range(3,12).Avg“ ist hier der Mittelwert der bekannten Januare 2018, 2019 und 2020.

Ich addiere zum Mittelwert das 24-fache der Steigung (24 ergibt sich, weil der Januar 2018 36 Monate vom Prognosemonat Januar 2021 entfernt ist, Januar 2019 24 Monate und Januar 2020 12 Monate, das macht dann im Durchschnitt 24) und erhalte die Prognose, die auch bei den Vorschauwerten steht:

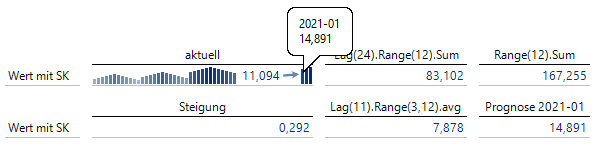
Prognose für Januar 2021

Obwohl die Kennzahl zum Jahresende immer fällt, kann der positive Sprung zum Januar vorhergesagt werden. Für die Vorschauwerte muss dabei der Zyklus auf 12 eingestellt sein.

Es ließe sich auch ein „Nowcast“ erstellen, indem nur die Monate bis zum Vormonat für eine Prognose des aktuellen Monats benutzt werden und Auffälligkeiten könnten als Differenz zwischen Nowcast und tatsächlichem Wert definiert werden. Wie anfangs versprochen öffnen die benutzerdefinierten Zeitanalyseelemente – in Kombination mit daraus abgeleiteten berechneten Elementen – ein Tor zu einem neuen Universum mit vielen Möglichkeiten!