Unternehmen, die für ihren Vertrieb die Nachfrage von Produkten oder für die Lagerhaltung und Produktion den Verbrauch von Materialien genauer vorhersagen können, sparen Kosten und haben Vorteile im Wettbewerb. In Projekten zum Thema „Predictive Analytics“, wie Prognosen heute heißen, beschäftigen uns immer wieder die Maße, mit denen man Vorhersagbarkeit misst. Heute widmen wir uns der Frage, was der Variationskoeffizient in XYZ-Analysen kann.

Beispielsweise in der Lagerhaltung werden benötigte Materialien nach der Regelmäßigkeit des Verbrauchs klassifiziert. Die XYZ-Analyse verwendet den Variationskoeffizienten, also den Quotienten aus Standardabweichung und Mittelwert, um die Konstanz des Verbrauchs zu beurteilen. Nahezu konstante Entnahmen landen in der X-Klasse, mittelmäßig schwankende Verbräuche in der Y-Klasse und der zu stark variierende Rest in der Z-Klasse. Die folgende Abbildung zeigt mögliche Verläufe dieser drei Fälle:

Mögliche Verläufe der drei XYZ-Klassen

In DeltaMaster lassen sich die Variationskoeffizienten über den Menüpunkt Spaltenaggregationen einfach berechnen:

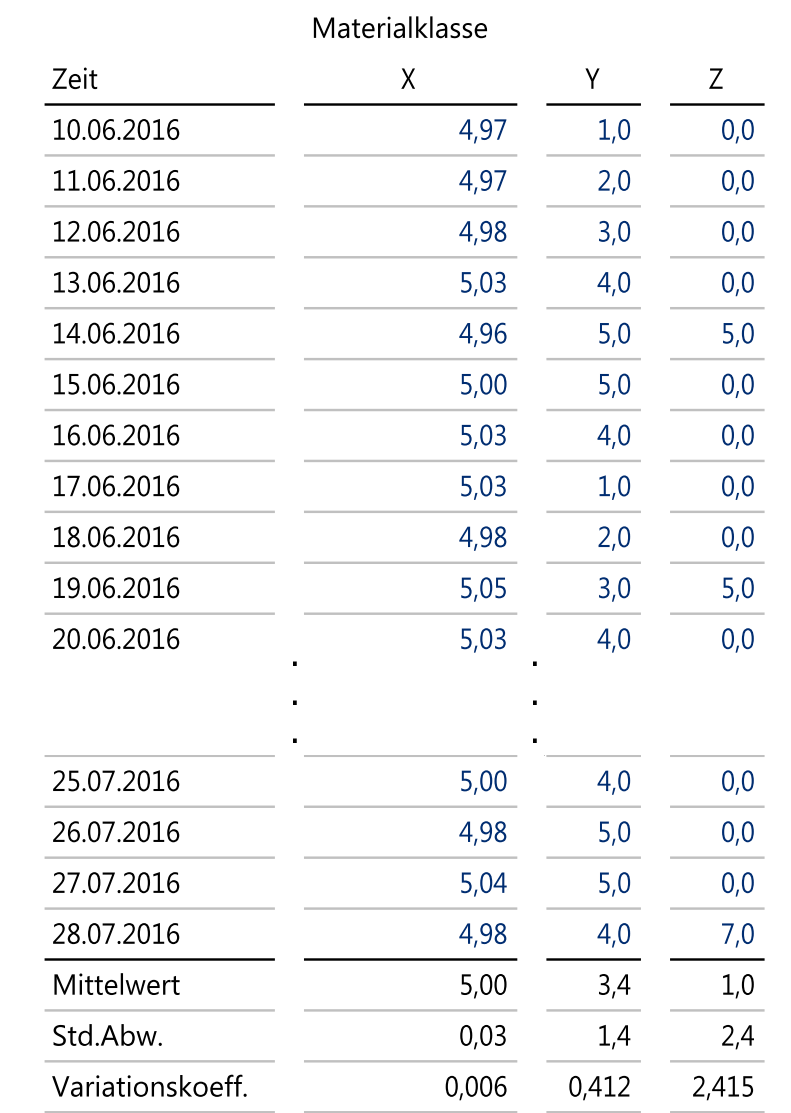
Variationskoeffizienten

Im Rahmen der XYZ-Analyse und im Zusammenhang mit der Planung werden diese Klassen gerne einmal in direkte Beziehung zum Grad der Vorhersagbarkeit gesetzt.

Zwei Fragen stellen sich hier sofort: Ist der Variationskoeffizient ein hinreichend informativer Indikator für die Verlaufsform wie z. B. die der Y-Klasse zugewiesenen “Schwankungen aus saisonalen Gründen” und hat er etwas mit der Vorhersagbarkeit der Zeitreihe zu tun?

Auf jeden Fall gilt, dass ein sehr niedriger Variationskoeffizient in der Tat aussagekräftig ist und auf einen relativ konstanten Verbrauch (im Vergleich zum Durchschnittsverbrauch!) hindeutet. Eine Zeitreihe, die nahezu konstant ist, lässt sich natürlich auch mit geringem Fehler gut vorhersagen.

Im Fall unseres Y-Materials ist festzustellen, dass hier der Verbrauch nicht konstant ist, wie auch der Variationskoeffizient richtigerweise erkennt. Jedoch lässt sich der Verbrauch perfekt vorhersagen, da er sich im Wochenrhythmus (1-2-3-4-5-5-4) ohne jegliche Veränderung identisch wiederholt.

Wenn man die beobachteten Y-Werte sortiert (YS) oder zufällig permutiert (YP), ergibt sich das folgende Bild:

Permutation (YP) und Sortierung (YS) von Y – der Variationskoeffizient bleibt gleich!

Sämtliche drei Zeitreihen führen jedoch zum gleichen Wert des Variationskoeffizienten. Das heißt, der hier gegebene, mittelgroße Variationskoeffizient trifft sowohl auf eine perfekt vorhersagbare Zeitreihe (Y), auf eine relativ gut vorhersagbare ZTR (YS) und eine nur mit großer Streuung vorhersagbare Zeitreihe (YP) zu.

Bleibt das Z-Material der ersten Grafik zu betrachten: Auf den ersten Blick gibt es unterschiedlich große Ausschläge, die auch noch in unterschiedlich langen zeitlichen Abständen erfolgen. Hier ist wohl tatsächlich nichts zu machen – oder?

Stellen wir uns einmal vor, dass es sich hier um Bestellmengen eines einzelnen Kunden handelt. Um den Leser nicht allzulang auf die Folter zu spannen, verraten wir hier die Generierung der Daten:

Es wird angenommen, dass der Kunde jeden Tag den gleichen Verbrauch hat, nämlich genau eine Einheit. Er füllt den Vorrat aber nicht jeden Tag auf, sondern die Abstände der Bestellungen sind zufällig. Im obigen Beispiel ist also doch eine gewisse Stabilität – trotz des großen Variationskoeffizienten – vorhanden, wenn man das System durchschaut hat:

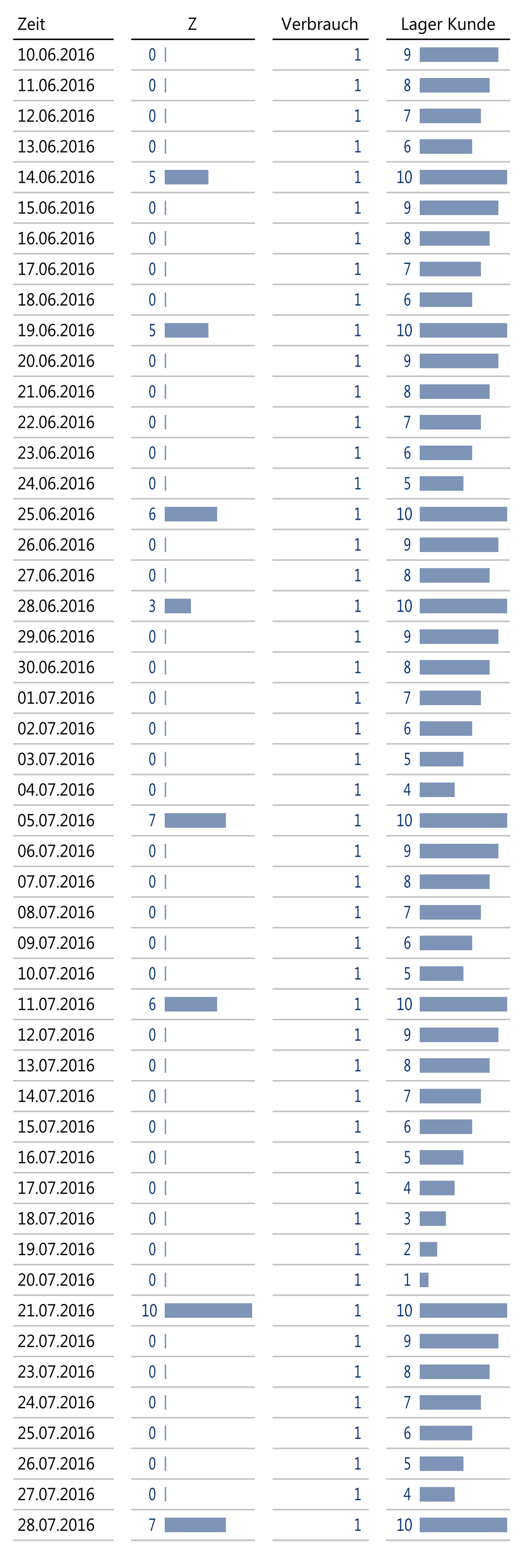
Planungssicherheit auch in der Z-Klasse

Der Kunde kommt somit in unterschiedlich großen zufälligen Abständen an, kauft aber immer die Menge ein, die seinen Lagerbestand am Ende des Tages auf 10 bringt. Diese Menge entspricht exakt der Anzahl der Tage seit dem letzten Besuch.

Natürlich kann man sich über diese Einkaufsstrategie allein durch Beobachtung nie sicher sein, aber als Arbeitshypothese geht man nun so vor, dass für jeden Tag der Verbrauch von 1 in der Planung berücksichtigt wird. Es gibt dann zwar die Unsicherheit über den Tag des Erscheinens des Kunden, aber die von ihm verlangte Menge kann immer exakt zur Verfügung gestellt werden.

Somit kann auch trotz eines hohen Variationskoeffizienten Planungssicherheit vorherrschen. Es ist sicherlich auch interessant, Bestellmuster der Kunden zu erkennen und zu gruppieren, aber dieses Thema sollte in einem zukünftigen Blogbeitrag behandelt werden.

Bei der XYZ-Methode bleibt zu vermelden, dass nur die Konstanz der X-Klasse ein hinreichendes Argument für gute Vorhersagbarkeit darstellt. Aber selbst hier muss die Annahme stimmen, dass sich die Struktur der Zeitreihe nicht oder zumindest nur sehr langsam ändert.

Im allgemeinen Fall bedeutet ein komplexes Aussehen allein jedenfalls noch nicht, dass keine gute Vorhersage möglich ist – vielleicht hat man ja bloß noch nicht die richtige Formel gefunden!