Process Mining erlaubt die Analyse von Geschäftsprozessen, die im Zeitalter der Digitalisierung häufig in Form von computergenerierten Log-Files protokolliert werden. Wir zeigen im heutigen Beitrag einige Szenarios, in denen DeltaMaster einen Mehrwert bei der Interpretation der Prozesse liefert.
Process Mining auf Basis von Log-Files
Jeder Geschäftsprozess besteht im Grunde genommen aus einer Abfolge von Aktivitäten, die zu bestimmten Zeitpunkten beginnen und enden, unterschiedliche Ressourcen binden und weitere sonstige Eigenschaften besitzen können. Häufig liegt ein Log-File vor, in dem die Schritte in einer einheitlichen Form automatisch abgespeichert werden.
Entweder wird dieses direkt erzeugt oder es kann aus anderen Aufzeichnungen abgeleitet werden.
Zu Illustrationszwecken verwenden wir in diesem Beispiel – per Simulation generierte! – Daten aus dem Supportcenter eines fiktiven Unternehmens. Im Log-File könnten die Schritte in der folgenden Form erscheinen:
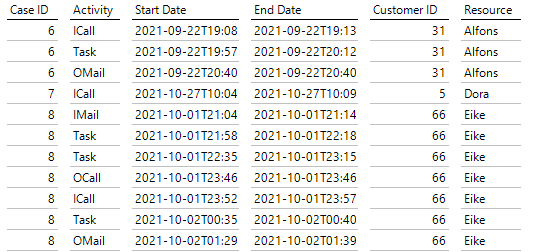
Ein Log-File als Ausgangspunkt des Process Mining
Unentbehrlich sind hier die Case ID, die einen Vorgang eindeutig beschreibt, die zugehörigen Aktivitäten und schließlich die Zeitstempel, die diese Aktivitäten zu einem Fall in eine zeitliche Reihenfolge bringen. Hier wurde vereinfachend angenommen, dass die Aktivitäten zu einem Supportfall jeweils nur von einer Person stammen und deshalb keine Überlappungen vorliegen können.
Dazu gibt es optional Angaben über gebundene Ressourcen – hier der zuständige Mitarbeiter aus dem Support – und weitere Angaben, etwa über den Kunden. Insgesamt liegen im Datensatz 2000 Supportfälle vor.
Im Beispiel gibt es keinen eigenen Eintrag für den Abschluss eines Supportfalls. Dies kommt bei Log-Files häufiger vor; zum Beispiel meldet sich der Besucher einer öffentlichen Webseite auch nicht explizit ab.
Es gibt bei diesem Beispiel insgesamt 5 Aktivitäten ICall, IMail, OCall, OMail und Task. ICall und IMail bezeichnen eingehende Anrufe oder E-Mails des supportsuchenden Kunden, OCall und OMail stehen für die ausgehenden Entsprechungen und Task sei die Beschäftigung mit einem vom Kunden geschilderten Problem ohne dessen Anwesenheit.
Die vorliegende Analyse konzentriert sich auf den Netto-Aufwand an Zeit für einen Supportfall; somit betonen wir die interne Sicht des Unternehmens. Alternativ oder zusätzlich könnte man auch die Bruttozeit von Beginn bis Ende des Supportfalls betrachten.
Process Maps
Im vorliegenden Blog-Beitrag möchten wir unseren Supportprozess erst einmal verstehen: Wir schauen auf einen wichtigen Teilaspekt im Process Mining, nämlich herauszufinden, in welcher Form typische Supportfälle ablaufen oder welche Abfolgen am häufigsten auftreten. Bevor wir auf Möglichkeiten der Analyse in unserer Business-Intelligence-Software DeltaMaster schauen, werfen wir einen Blick auf grafische Darstellungen, wie sie bei Process Mining häufiger auftreten.
Hierzu habe ich einmal die bestehenden Möglichkeiten der Programmiersprache R eruiert und das R-Package bupaR (Business Process Analytics in R, Quelle am Seitenende) hergenommen. Zu der typischen Ausgabe gehört die Process Map:
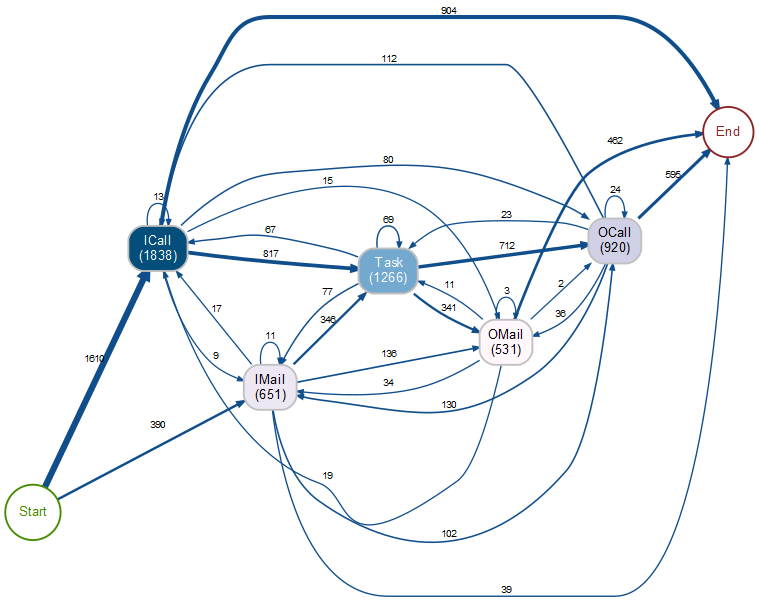
Process Map in bupaR
In dieser Darstellung geben die Zahlen in den Knoten an, wie häufig Aktivitäten stattfinden, und die Zahlen an den Kanten besagen, wie häufig die zwei benachbarten Aktivitäten in der gegebenen Reihenfolge aufeinanderfolgen.
Auch wenn diese Darstellung hilfreich sein kann, sagt sie nicht aus, wie oft bestimmte komplette Folgen von Aktivitäten stattfinden. In der Abbildung ist ersichtlich, dass 1610 der 2000 Fälle mit einem ICall beginnen und 904 Fälle mit einem ICall enden, aber es ist hier nicht ablesbar, wie viele Fälle exakt aus einem einzigen ICall bestehen.
Ein weiteres Beispiel: 341-mal folgt auf Task eine ausgehende OMail, aber 462-mal ist eine OMail die letzte Aktivität in einem Fall, also deutlich mehr. Wir können aber aus der Abbildung nicht die Vorgeschichte dieser 462 Fälle ablesen.
Woran liegt es, dass wir aus den sichtbaren Zahlen nicht die Fallzahlen mit einem gegebenen Verlauf wie etwa ICall → Task → OMail ermitteln können?
Verantwortlich sind hier Stränge, die sich in einem Knoten wieder treffen und – noch hinterhältiger – Aktivitäten, die mehrfach ausgeführt werden. Hier müssen dann Rückverbindungen existieren, die wieder auf einen bereits durchlaufenen Knoten zeigen.
Um die Problematik zu illustrieren, schauen wir einmal auf die folgenden zwei Beispiele.
Grenzen der Process Map
Das erste Beispiel A sieht so aus:
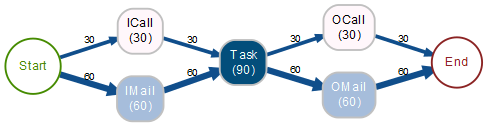
Irreführende Process Map A
Bei Betrachtung dieses Graphen glaubt man, dass es wohl zwei typische Folgen “ICall → Task → OCall” und “IMail → Task → OMail” gibt, wobei 30 Fälle zu der ersten Kategorie gehören und 60 Fälle zur zweiten. In Wirklichkeit habe ich aber sämtliche 30 Fälle, die über ICall nach Task gelangen, mit OMail fortsetzen lassen und die 60 Fälle, die über IMail in Task münden, je zur Hälfte auf OCall und OMail verteilt.
Die Process Map, wie sie hier vorliegt, hat kein Gedächtnis und kann die Vorgeschichte nicht berücksichtigen.
Oder betrachten wir den folgenden, vermeintlich einfachen Graphen:
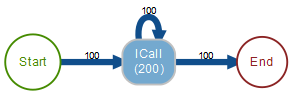
Irreführende Process Map B
Hier könnte man annehmen, dass es 100 Fälle gab, die jeweils mit 2 ICalls erledigt waren. Aber auch 99 Fälle mit einem ICall und 1 Fall mit 101 ICalls wären möglich.
Übrigens waren es tatsächlich 51 Fälle mit 1 x ICall, 20 Fälle mit 2 x ICall, 19 Fälle mit 3 x ICall, 5 Fälle mit 4 x ICall, 1 Fall mit 5 x ICall, 2 Fälle mit 6 x ICall und jeweils 1 Fall mit 7 x ICall und 8 x ICall: 51*1 + 20*2 + 19*3 + 5*4 + 1*5 + 2*6 + 1*7 + 1*8 = 51 + 40 + 57 + 20 + 5 + 12 + 7 + 8 = 200.
Es gibt nur eine Konstellation, bei der die Process Map immer die vollständige Information liefert: wenn ein Baum vorliegt!
Process Mining bei einem Baum
Bei einem Baum wie im folgenden Beispiel werden im Zeitverlauf nur Knoten angesteuert, die sich auf einem einzigen Weg erreichen lassen (der aggregierende End-Knoten, der den Abschluss der Folgen signalisiert, wird hier nicht mitgezählt!):
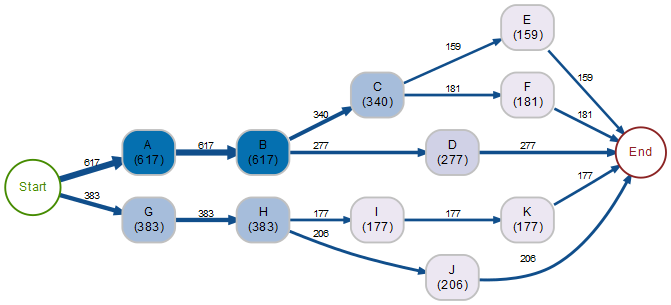
Sämtliche Prozessschritte lassen sich klar ablesen
617 Fälle beginnen mit der Kombination A → B, davon werden 340 mit C und hiervon 159 mit E fortgesetzt. Die Folge A → B → C → E liegt somit in 159 Fällen vor.
Durch einen Trick lässt sich nun jede Process Map in einen Baum verwandeln.
Process Map in einen Baum transformieren
Wenn man anstelle einer Aktivität die gesamte Vorgeschichte mit in die neue “Aktivität” aufnimmt, ergibt sich automatisch ein Baum. Liegt eigentlich eine Folge A → B → A → C vor, betrachten wir nun ersatzweise die Folge A → AB → ABA → ABAC. Die tatsächlichen Aktivitäten lassen sich immer noch ablesen (es ist das letzte Element im String), es kann keine Schleifen geben, da die Folge mit jedem Schritt immer länger wird und zwei Folgen können nur in einem gemeinsamen Knoten landen, wenn die Vorgeschichte übereinstimmt. Dann sind sie sogar bis zu diesem Schritt identisch.
Wendet man nun diese Transformation etwa auf das Beispiel A an, so sieht man meine erwähnte Manipulation:
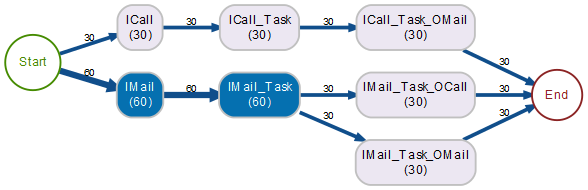
Auf ICall folgt immer OMail
Auch beim Beispiel B lässt sich nun leicht ablesen, wie viele ICalls denn tatsächlich stattgefunden haben. Da es nur um ICalls geht, genügt eine Bezeichnung “n. ICall”, mit n = Anzahl der ICalls:
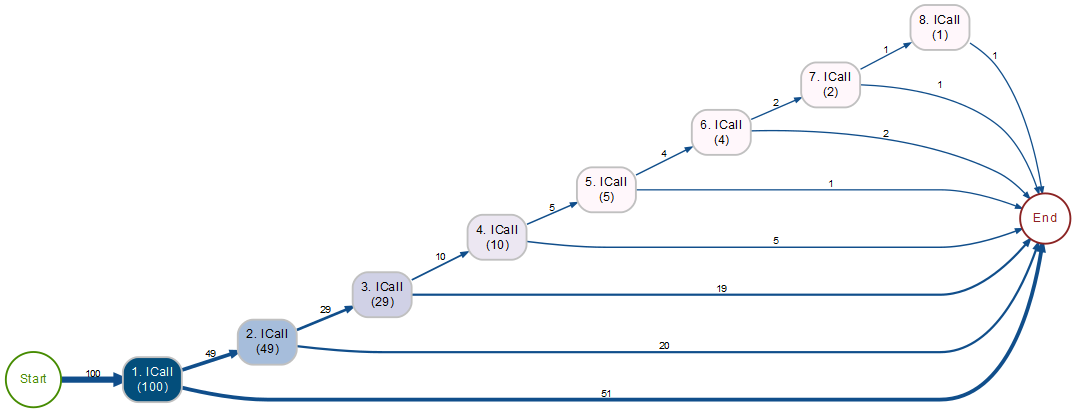
Ablesen, wie oft ICalls vorkamen
51 Fälle waren nach dem 1. ICall beendet, 49 Fälle benötigten weitere ICalls. Mit dem 2. ICall waren 20 Fälle erledigt usw.
Einschränkungen für das Process Mining
Allerdings gibt es bei diesem Ansatz auch unwillkommene Änderungen: Die Häufigkeit einer Aktivität lässt sich nicht mehr so schnell ablesen, sondern muss aus mehreren Knoten addiert werden. Bestimmte Operationen wie das Eliminieren seltener Aktivitäten für die Analyse oder das Einschränken auf Folgen, die etwa eine Aktivität A enthalten und später eine Aktivität B, werden nun schwieriger.
Auch steigt die Anzahl der Knoten schneller an, sodass ein Graph für reale Beispiele zu unübersichtlich wird.
Es gibt auch Anwendungen, bei denen jeder Zweig nach ein paar Schritten nur noch jeweils einen Fall beschreiben würde, das heißt, jede Prozessfolge kann ein Unikat sein.
Wenn aber wie in unserem Supportbeispiel wenige Aktivitäten vorliegen, die allesamt für die Analyse relevant sind, und wir davon ausgehen können, dass bestimmte Prozessfolgen doch gehäufter auftreten werden, dann bietet der Ansatz Vorteile.
Allerdings wollen wir die Analyse ohne graphische Darstellung durchführen (sie ließe sich über gespeicherte Prozeduren im SQL-Durchgriff wie im Beitrag Bilder in Berichten beschrieben mit etwas Aufwand hinzufügen).
Die zwei Varianten, die ich gleich vorstellen werde, bauen aber beide auf dem Baumansatz auf.
Process Mining mit Parent-Child-Hierarchien
Für die interne Darstellung zur Modellierung verwende ich hier in unserer BI-Software DeltaMaster die folgende Zuordnung von Buchstaben zu den Aktivitäten: A (IMail), B (OMail), C (ICall), D (OCall) und E (Task). Dazu kommt noch ein Z für einen abgeschlossenen Fall.
Ein noch nicht abgeschlossener Fall mit ICall und Task wird daher intern mit “CE” identifiziert und ein bereits mit einem einzigen ICall abgeschlossener Fall ist als Element “CZ” gespeichert. Dazu kommen Elementeigenschaften für die Anzeige. Hier bieten sich als Bezeichner einmal die letzte Aktivität und einmal die komplette Folge an.
Im folgenden SQL-Durchgriff sind exemplarisch einige Zeilen der Definition der Parent-Child-Hierarchie zu sehen:
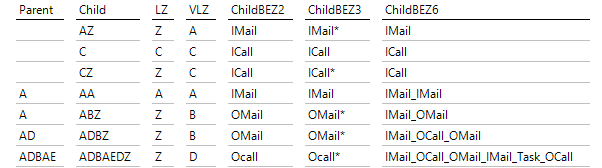
Definitionen der PC-Hierarchie
Die Elemente in der Child-Spalte sind dann in DeltaMaster zu sehen. Ein Element, das ja einer Teilfolge entspricht, wird unter demjenigen Element eingehängt, das der vorhergehenden Teilfolge entspricht, bei der die letzte Aktivität noch fehlt. LZ steht hier für das letzte Zeichen und dient zur Fallunterscheidung, um die letzte Aktivität (in VLZ) anzuzeigen.
Mehr zum Vorgehen der Modellierung der PC-Hierarchie gibt es im Beitrag Parent-Child-Hierarchien im Selfservice nachzulesen.
Process Mining – die Analysen
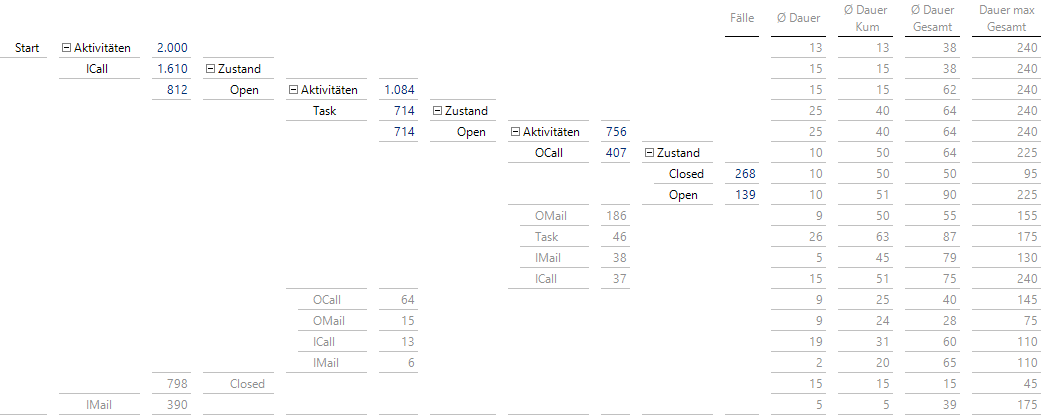
Nun lassen sich die einzelnen Folgen analysieren: Wie viele gibt es jeweils von einer Sorte und wie lange dauern die Vorgänge im Schnitt oder maximal:
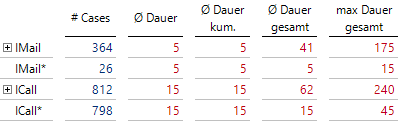
Anzahl und Dauer von Vorgängen
Hier müssen kumulierte Dauer bis zur gezeigten Aktivität und Gesamtdauer vorberechnet sein, da eine Einzelzeitdauer einem Knoten zugeordnet wird und sich nicht durch Aggregation von Werten der Blätter des Hierarchiebaumes ergibt. Die automatische Aggregation ist somit in den Hierarchieeigenschaften deaktiviert. Ein “*” kennzeichnet einen abgeschlossenen Supportfall; wir benutzen hier als Alias den Bezeichner ChildBEZ3 aus dem obigen SQL-Durchgriff.
Mit etwas mehr Aufwand hätte man die vier gezeigten ersten Aktivitäten auch noch unter einem gemeinsamen Knoten verankern können.
Hier sieht man nun, dass 798 Supportfälle mit einem einzigen ICall erledigt waren, der im Schnitt 15 min dauerte. Es gab aber auch Fälle, die 45 min dauerten.
Wenn man sehen will, welche Folgen am häufigsten vorkommen, bietet sich eine ABC-Analyse an, auf die man die unterste Ebene (hier sind es 15 Ebenen) der Child-Dimension zieht. Dazu muss man wissen, dass Blätter von vorzeitig endenden Ästen intern als 1:1-Kopie an die nachfolgende Ebene weitergereicht werden. Sie stehen dann auch in der untersten Ebene zur Verfügung. Weiterhin hat man so sichergestellt, dass alle Folgen abgeschlossen sind, also in der internen Darstellung mit Z enden.
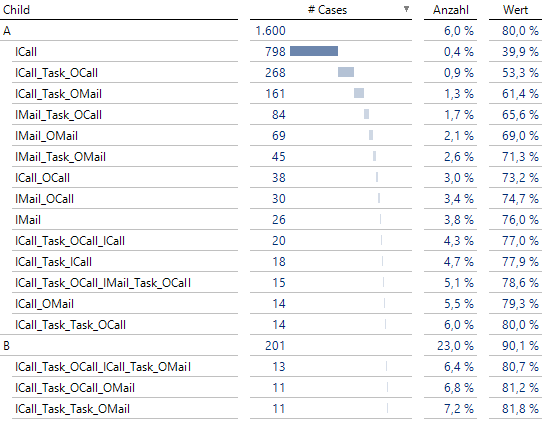
ABC-Analyse mit den häufigsten Folgen
Hier haben wir in den Einstellungen bei den Elementeigenschaften als Alias die lange Bezeichnung ChildBEZ6 als Beschriftung gewählt.
Neue Option bei der ABC-Analyse
Übrigens lassen sich seit dem Release 6.4.1.1 die Klassengrenzen auch selbst einstellen (Optionsmenu mit F4 aufrufen und Reiter Klassen anwählen):
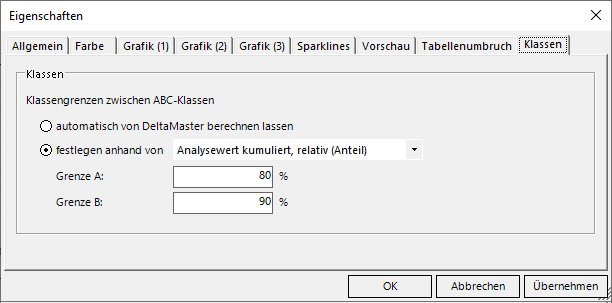
ABC-Analyse; A-Klasse mit 80 Prozent
Process Map in bupaR
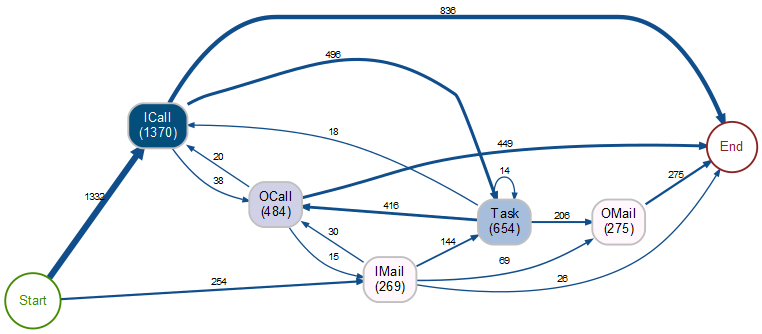
Auch das bupaR-Paket bietet als Option an, eine vereinfachte Process Map nur der am häufigsten auftretenden Prozessketten (die hier ebenfalls 80 % der Fälle abdecken) zu erzeugen:
Wie bupaR die häufigsten Prozessfolgen sieht
Wie bereits beschrieben, lassen sich aus diesem Graphen nicht die Fallanzahlen einzelner Folgen rekonstruieren. Schauen wir hingegen auf die ABC-Analyse, so sehen wir, dass zum Beispiel die 836 Fälle in der Process Map, die mit einem ICall enden, durch die Folgen ICall (798), ICall_Task_OCall_ICall (20) und ICall_Task_ICall (18) gegeben sind.
Auch die sichtbaren 206 Übergänge von Task nach OMail lassen sich nun erklären: Sie stammen aus den Folgen ICall_Task_OMail (161) und IMail_Task_OMail (45).
Nun lässt sich mit Multiples und Verknüpfungen eine kleine Anwendung bauen:
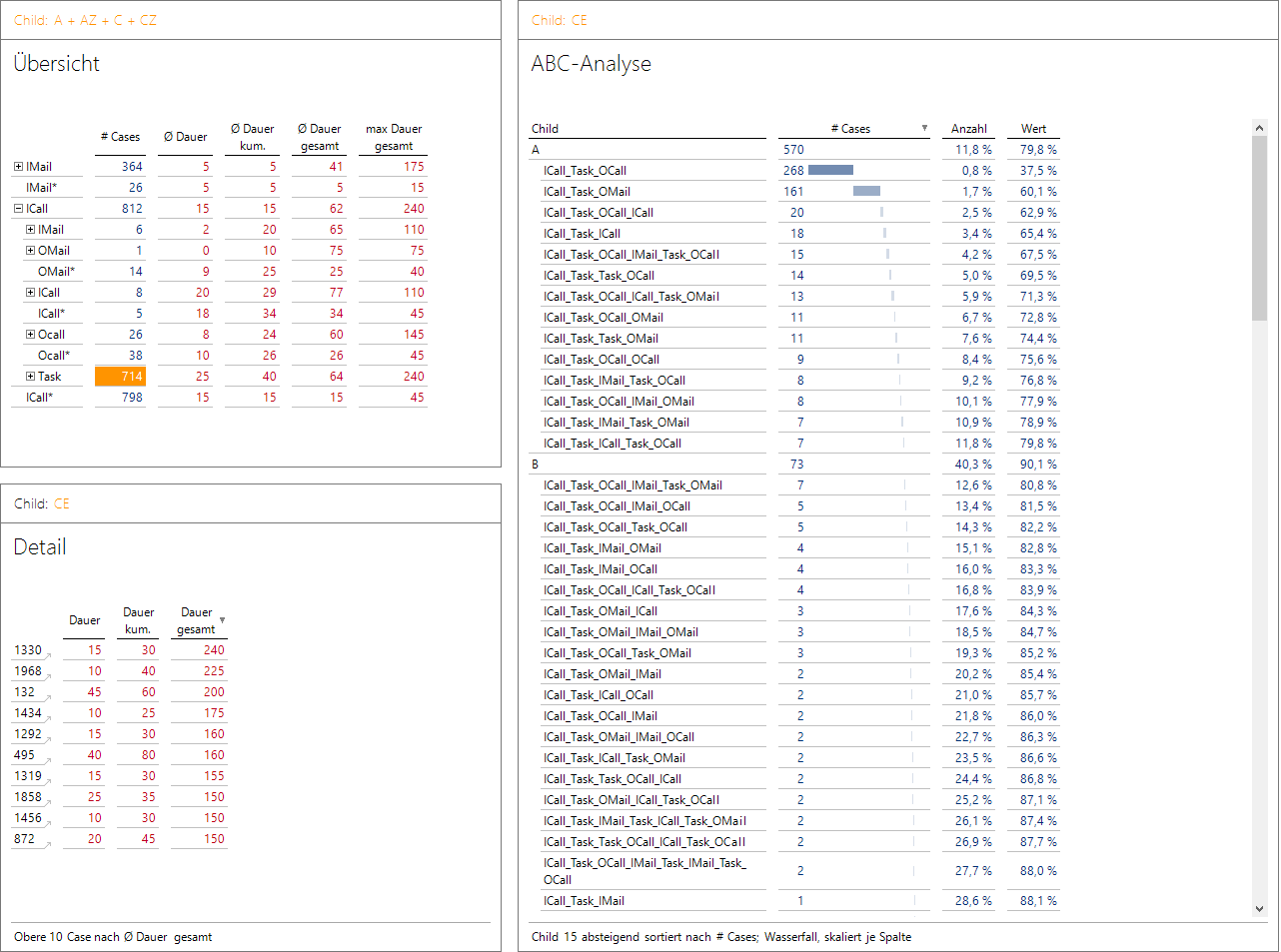
Analyse des Support-Prozesses
In der Übersicht sehen wir, dass Supportfälle, die mit ICall_Task anfangen, mit 64 Minuten im Schnitt doch recht lange dauern und auch mit 240 Minuten den längsten Fall aufweisen. Ein Strg + Linksklick markiert die Zelle und überträgt den Filter (intern CE für ICall_Task) auf die anderen Berichte. Die ABC-Analyse zeigt nun die Häufigkeiten der möglichen Fortsetzungen.
Die meisten Fälle sind mit dem folgenden OCall oder der versandten OMail beendet. Mit 2 von 119 (= 1,7 %) möglichen Prozessfolgen werden bereits 429 von 714 Fällen (= 60,1 %), die mit ICall_Task beginnen, abgedeckt.
Links unten werden die 10 Fälle mit der längsten Dauer angezeigt. Ein Klick auf die Verknüpfung bei Fall 1330 zeigt uns die Liste der Aktivitäten:
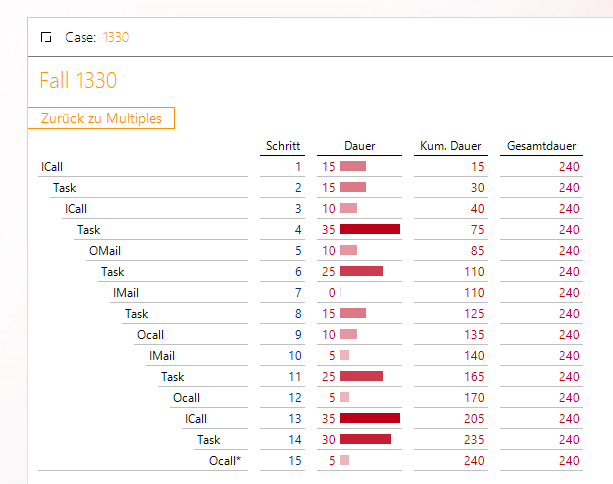
Die einzelnen Schritte des Falls 1330
In diesem Fall haben wir eine Grafische Tabelle genutzt, möglich wäre auch ein SQL-Durchgriff.
Auch in bupaR existiert mit “traces” ein Befehl, der die Häufigkeiten von Folgen berechnet, allerdings gibt es dort nicht die Interaktion wie in unserem schönen Multiples-Beispiel.
Navigation im Netzwerk
Ein weiterer interessanter Ansatz ist durch die Netzwerknavigation gegeben, die seit dem Release 6.3.3 auch für relationale Anwendungen – eine solche verwende ich in diesem Beispiel – zur Verfügung steht. Dazu werden die vordefinierten Schritte einer Navigation in einer Grafischen Tabelle verwendet.
Das Datenmodell muss bestimmte Eigenschaften aufweisen: Wir brauchen eine Quell- und eine Zieldimension, die aber beide eigentlich inhaltlich gleiche Elemente beschreiben; nur die Rolle in einem Paar zweier Elemente wird unterschiedlich interpretiert.
Zum Beispiel könnten es Start- und Endpunkte von Transporten sein, die beide durch Orte gegeben sind. Die Kennzahl beschreibe hier Stückanzahlen oder Mengen.
Dazu benötigen wir eine weitere Dimension, die hier den Typ der Beziehung weiter differenziert. Im Transportbeispiel könnte dies die Transportart sein – Bahn, LKW, Flugzeug… – oder die eingesetzte Spedition oder die Produktgruppe usw.
Process Mining mit Netzwerknavigation im Supportbeispiel
In unserem Supportbeispiel werden wir die Parent- und die Child-Dimension – wie oben bereits eingesetzt – als Quell- und Zieldimension verwenden, bloß modellieren wir keine Parent-Child-Hierarchie, sondern bleiben bei zwei flachen Listen in eigenen Dimensionen. Man hätte Parent/Child hier auch Source/Sink, Quelle/Ziel oder Von/Nach nennen können.
Dazu kommt die Aktivität als dritte Dimension.
Typische Zeilen zu einem Vorgang sehen dann so aus:
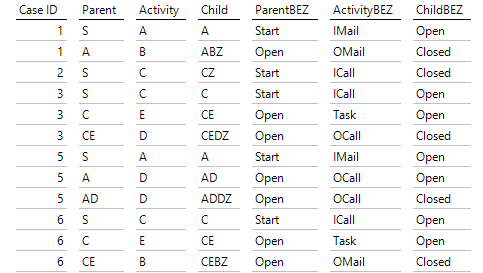
Die drei benötigten Dimensionen und Bezeichner für die Anzeige
Parent, Activity und Child definieren die drei benötigten Dimensionen und in den rechten Spalten stehen sprechende Bezeichner, die wir für die Anzeige verwenden werden. Die Grundidee der Navigation ist nun, dass ein Child eines Vorgangs als Parent einer Fortsetzung erscheinen kann:
Zum Beispiel startet Case 3 mit der Aktivität C und endet in Child = C. In der nächsten Zeile wird aus diesem C ein Parent und mit der Aktivität E entsteht ein Child CE. Dieses kann wieder als Parent interpretiert werden und mit Aktivität D erhalten wir zunächst ein Child CED. Da die Folge hier beendet ist, fügen wir ein Z an. Jedes Child mit Ende “Z” erhält den Bezeichner ChildBEZ = Closed.
In einer Grafischen Tabelle starten wir nun mit dem Start-Element aus der Parent-Dimension und führen zwei Navigationsschritte nach Activity und Child aus. Rechts unter Editieren finden wir den Punkt Navigation und wir speichern auf dem Reiter “Vordefinierte Navigationsschritte” diese zwei Schritte als Default ab. Anschließend aktivieren wir die Checkbox “Vordefinierte Navigationsschritte als Netzwerk behandeln”:
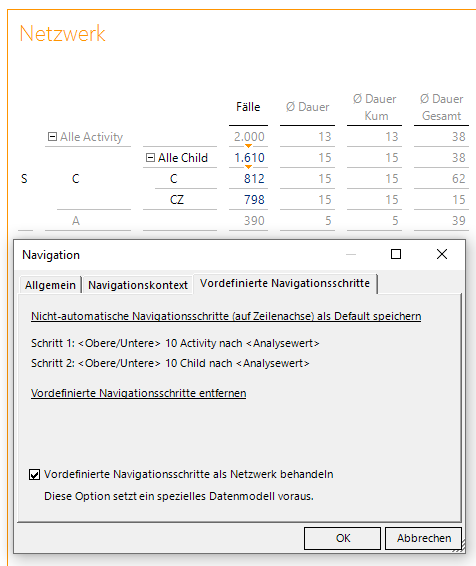
Vordefinierte Navigationsschritte als Netzwerk behandeln
Danach klappen wir den Baum wieder zu und verschönern die Ansicht, indem wir ab jetzt die Bezeichner verwenden und “Alle Activity” durch “Aktivitäten” und “Alle Child” durch “Zustand” ersetzen.
Interaktives Process Mining mittels Netzwerknavigation
Im Navigationsmodus können wir uns nun durch einfache Doppelklicks auf die Zahlenwerte durch das Netzwerk bewegen:
Ausgangssituation mit Überblick aller Fälle
Klicken wir doppelt auf die 2000 Fälle, werden automatisch die möglichen Aktivitäten ausgeklappt, die hier im 1. Schritt nur aus ICall und IMail bestehen können:
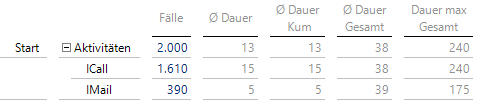
Supportfälle beginnen mit ICall oder IMail
Ein weiterer Doppelklick auf die 1610 zu ICall führt zu einem Zwischenstand der geöffneten und abgeschlossenen Fälle:
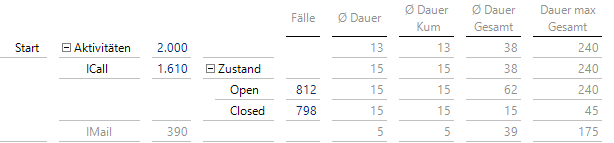
798 Supportfälle sind mit einem ICall abgeschlossen
Für die internen, abgeschlossenen Child-Elemente (sie erhalten ein “Z” als Ende) existiert kein analoges Element in der Parent-Dimension, da diese nur offene Fälle enthält, und somit ist eine weitere Navigation nicht möglich. Es erscheint eine Warnung:
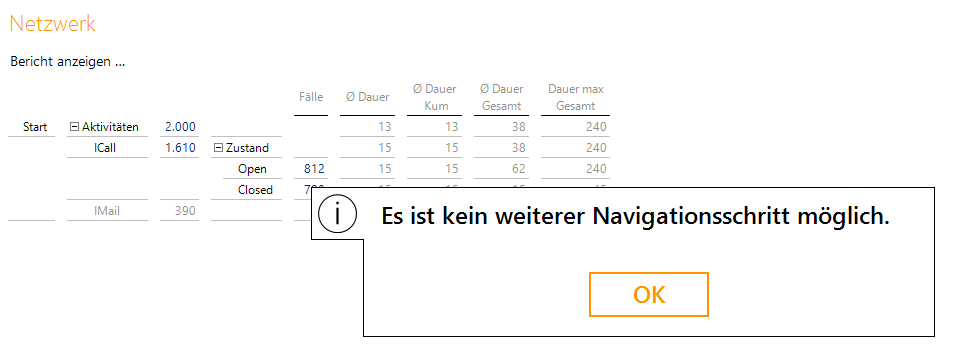Warnung, wenn der Pfad das Ende erreicht hat
Auf offenen Pfaden lässt sich die Navigation durch Doppelklicks beliebig fortsetzen:
Jeder Pfad kann einfach verfolgt werden
Da durchschnittliche und maximale Gesamtdauern immer sichtbar sind, können länger dauernde Aktivitätsfolgen einfach identifiziert werden.
Transitionsmatrix
Es lassen sich auch einfach Anzahlen von Übergängen berechnen (also ohne Berücksichtigung der Vorgeschichte), durch Anlegen zweier weiterer Dimensionen “Von” und “Nach”:
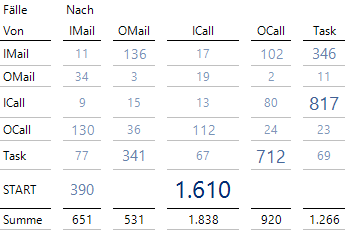
Die Matrix der Übergänge
Die Zahlen geben an, wie häufig Übergänge zwischen zwei Aktivitäten stattfinden und sind somit identisch zu den Werten an den Kanten der ersten Process Map ganz oben in diesem Artikel. Die Spaltensummen entsprechen den Werten in den Knoten und geben an, wie häufig eine Aktivität stattgefunden hat.
Dazu kann man eine kurze Tabelle der geschlossenen Fälle angeben, die dann den Werten an den Kanten zum End-Punkt entsprechen:
Geschlossene Fälle nach letzter Aktivität
Diese beiden Tabellen haben zusammen den gleichen Informationsgehalt wie die Process Map, die mit allen Fällen angelegt wurde.
Unter Einsatz des Zeileneditors lassen sich auch alle gezeigten Werte in einer Grafischen Tabelle unterbringen:
Alle Werte auf einen Blick
Die ersten 6 Zeilen zeigen die Häufigkeiten von Übergängen zwischen den Knoten inklusive Startknoten, die vorletzte Zeile gibt die Häufigkeiten einzelner Aktivitäten an und die letzte Zeile entspricht den Häufigkeiten der Übergänge zum Endknoten.
Quelle des R-Pakets bupaR
Gert Janssenswillen (2018). bupaR: Business Process Analysis in R. R package version 0.4.1. https://CRAN.R-project.org/package=bupaR
