In Zeitreihen erkennt das menschliche Auge beinahe mühelos, wenn Werte sich auf einem neuen Niveau einpendeln. Das gilt jedenfalls für sehr deutliche Muster. Können wir dem Rechner diese visuelle Kompetenz einhauchen? Werden sogar schwierigere Muster erkannt?

Gegeben sei eine Zeitreihe, die aus 42 Werten besteht. Wenn wir versuchen, sie in Segmente zu unterteilen, die sich durch unterschiedliche Niveaus auszeichnen, stellen sich zwei Fragen: Wie viele Segmente sollten wir nehmen und an welchen Stellen sollte die Zeitreihe zerlegt werden? Wir widmen uns hier der zweiten Frage, nehmen also die Anzahl der Segmente als gegeben an.

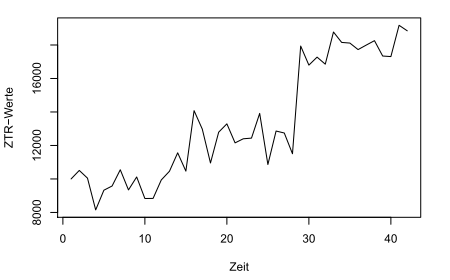
Mit bloßem Auge erkennen wir in diesen 42 Werten mehrere Phasen mit unterschiedlichen Wertniveaus

W. D. Fisher hat für dieses Problem 1958 folgendes vorgeschlagen (*): Trenne die Zeitreihe so, dass sich Werte innerhalb eines Segmentes möglichst ähnlich sind, d.h. wenig um den Mittelwert des Segments schwanken. Versuche dabei, die Summe der quadrierten Abweichungen zu minimieren.

Wie weit käme man allein durch systematisches Probieren? Bei 42 Werten gibt es 41 Stellen, an denen die Zeitreihe in 2 Segmente „aufgetrennt“ werden kann (zwischen 1 und 2, 2 und 3,…, 41 und 42). Nehmen wir eine Anzahl von 3 Segmenten als gegeben an, so benötigen wir 2 Trennstellen, die wir aus diesen 41 möglichen Trennstellen auswählen müssen. In unserem Beispiel gibt es dann genau

Möglichkeiten, die Zeitreihe aufzuspalten. Zur Berechnung der Aufteilung mit der kleinsten Summe der quadrierten Abweichungen hätte man den Algorithmus von Fisher noch nicht gebraucht. Unsere zweite  Grafik zeigt diese Aufteilung mit dem jeweiligen Mittelwert und jeweils +/- einer Standardabweichung.

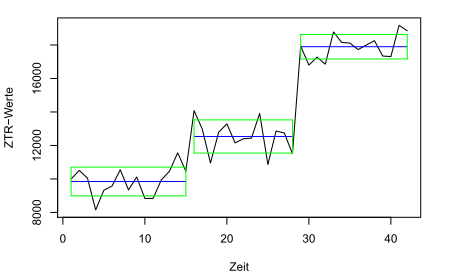
So wird die Zeitreihe segmentiert, wenn wir uns eine Aufteilung in 3 Segmente wünschen.

Bei 8 statt 3 Segmenten existieren bereits

Wahlmöglichkeiten für die 7 Trennstellen. Fishers Algorithmus ist schnell und findet in etwa einer Zehntelsekunde eine Lösung. Das Ergebnis sieht man in unserer dritten Grafik. Für diese Zeitreihe sind 8 Segmente wohl etwas zu viel (Dreiecke kennzeichnen singuläre Abschnitte mit nur einem Zeitpunkt).

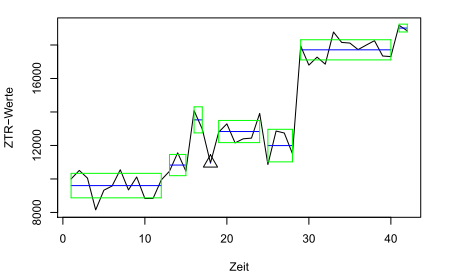
Die beste Aufteilung in 8 Segmente

Die Rechenzeit hängt vor allem von der Anzahl der Beobachtungen und der Anzahl der Segmente ab, weniger von den Werten der Zeitreihe. Die Trennung einer Zeitreihe mit z.B. 120 Monatswerten in 10 Segmente benötigt weniger als 1 Sekunde für die optimale Auswahl unter immerhin fast 10 Billionen möglicher Segmentierungen.

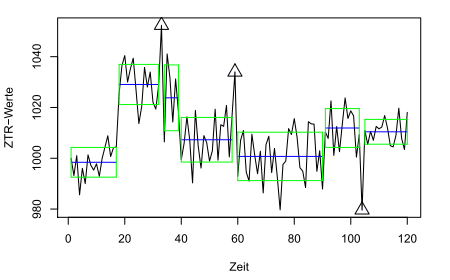
10 Jahre in 10 Segmenten in 1 Sekunde

In unserem Verfahren müssen wir die Anzahl der Segmente vorgeben. Das macht die Methode vor allem für interaktives Data Mining interessant. Die Rechenzeit steigt polynomial mit der Anzahl der Werte. Zeitreihen mit einer Länge von weniger als 200 Werten benötigen einige Sekunden für die Aufteilung. Eine Zeitreihe mit 1100 Werten (z.B. tägliche Daten für 3 Jahre) braucht etwa 90 Sekunden für eine Einteilung in 10 Segmente.

Daumen hoch oder runter? Mindestens als Assistent hat sich der Rechner qualifiziert. Die gefundenen Segmentierungen sind nachvollziehbar und leuchten ein.

Wir finden Fishers Idee sehr gut. Der Rechner hat visuelle Kompetenz bewiesen. Die Rechenzeit und das mathematisch nachvollziehbare Kriterium sprechen für sich. Können wir noch einen Schritt weitergehen und uns die Anzahl der Segmente errechnen lassen? Ein anderes Mal mehr dazu.

(*) W. D. Fisher. On grouping for maximum homogeneity. Jrnl. Am. Stat. Soc., 53:789,798, 1958