In sozialen Netzwerken wünscht sich der User, dass die von ihm veröffentlichten Beiträge möglichst weite Verbreitung finden. Wovon hängt es ab, wie viele Personen erreicht werden? Wann versandet eine Aktion?
Der Beitrag vom April 2017 Gute Freunde kann niemand trennen beschäftigte sich bereits mit sozialen Netzwerken, legte aber eher Wert auf die statischen Eigenschaften eines Netzwerks.
Hier wollen wir einmal auf die dynamischen Aspekte schauen und untersuchen, wie sich denn geteilte Beiträge verbreiten.
Im folgenden einfachen Netzwerk veröffentlicht die Person 7 eine Nachricht:
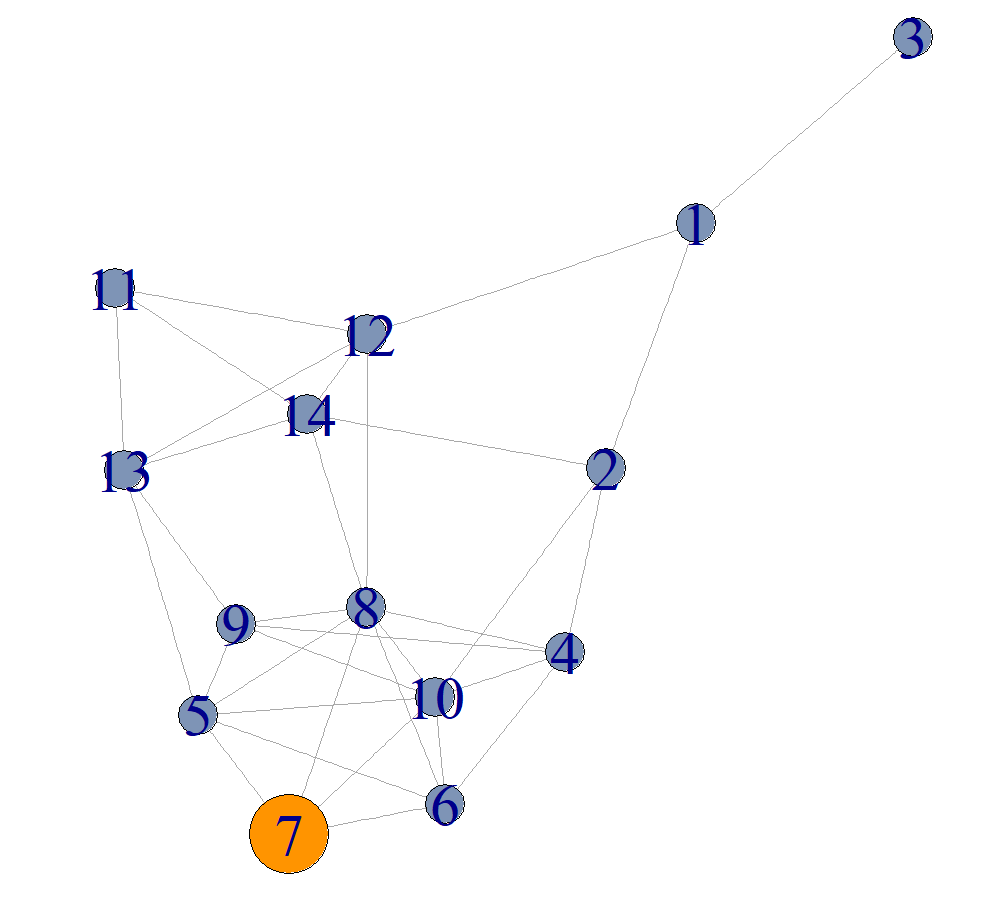
Person 7 möchte einen Beitrag verbreiten
Für die hier dargestellten Simulationen wählen wir die folgenden vereinfachenden Annahmen:
- Ein veröffentlichter Beitrag wird jedem Freund präsentiert.
- Jeder Empfänger teilt die Nachricht zu einem Zeitpunkt mit einer festen Wahrscheinlichkeit p, d. h.
- die Anzahl der eingehenden Verbindungen spielt keine Rolle; hier könnte man alternativ auch annehmen, dass die Wahrscheinlichkeit, einen bestimmten Beitrag zu teilen, mit der Anzahl der Verbindungen sinkt, da dieser dann leichter in der Informationsfülle untergeht.
- der Inhalt spielt hier keine Rolle; für eine komplexere Simulation müsste man Inhalt des Beitrags und Interessen des Empfängers berücksichtigen. Die Letzteren sind aber höchstens dem Betreiber des Netzwerks bekannt. Es gibt somit auch keine Werbeaktionen, die fremde Personen erreichen könnten.
- die Anzahl der Freunde, die diesen Beitrag geteilt und somit einer Person sichtbar gemacht haben, spielt keine Rolle: Eine Person wird weiterhin mit der festen Wahrscheinlichkeit p teilen. In einer aufwändigeren Simulation hätte man diese Anzahl auch noch berücksichtigen können.
- Die Aktivitäten erfolgen getaktet und synchron für alle Betroffenen:
- Phase 1: Die Nachricht trifft ein.
- Phase 2: Die Nachricht wird möglicherweise geteilt.
- Phase 3 ( = Phase 1 der nächsten Iteration): Geteilte Beiträge treffen bei den Freunden ein.
- …
Hier hätte man auch ein asynchrones Modell ansetzen können, das aber in der Simulation aufwändiger zu behandeln ist.
- Eine Person teilt einen Beitrag maximal einmal.
- Es gibt in diesem einfachen Modell keine Gruppen.
Schauen wir bei unserem Beispiel einmal an, wie sich der Beitrag verbreitet. Zunächst werden die Freunde aller Personen, die einen Beitrag erstellt/geteilt haben, in Grün dargestellt:
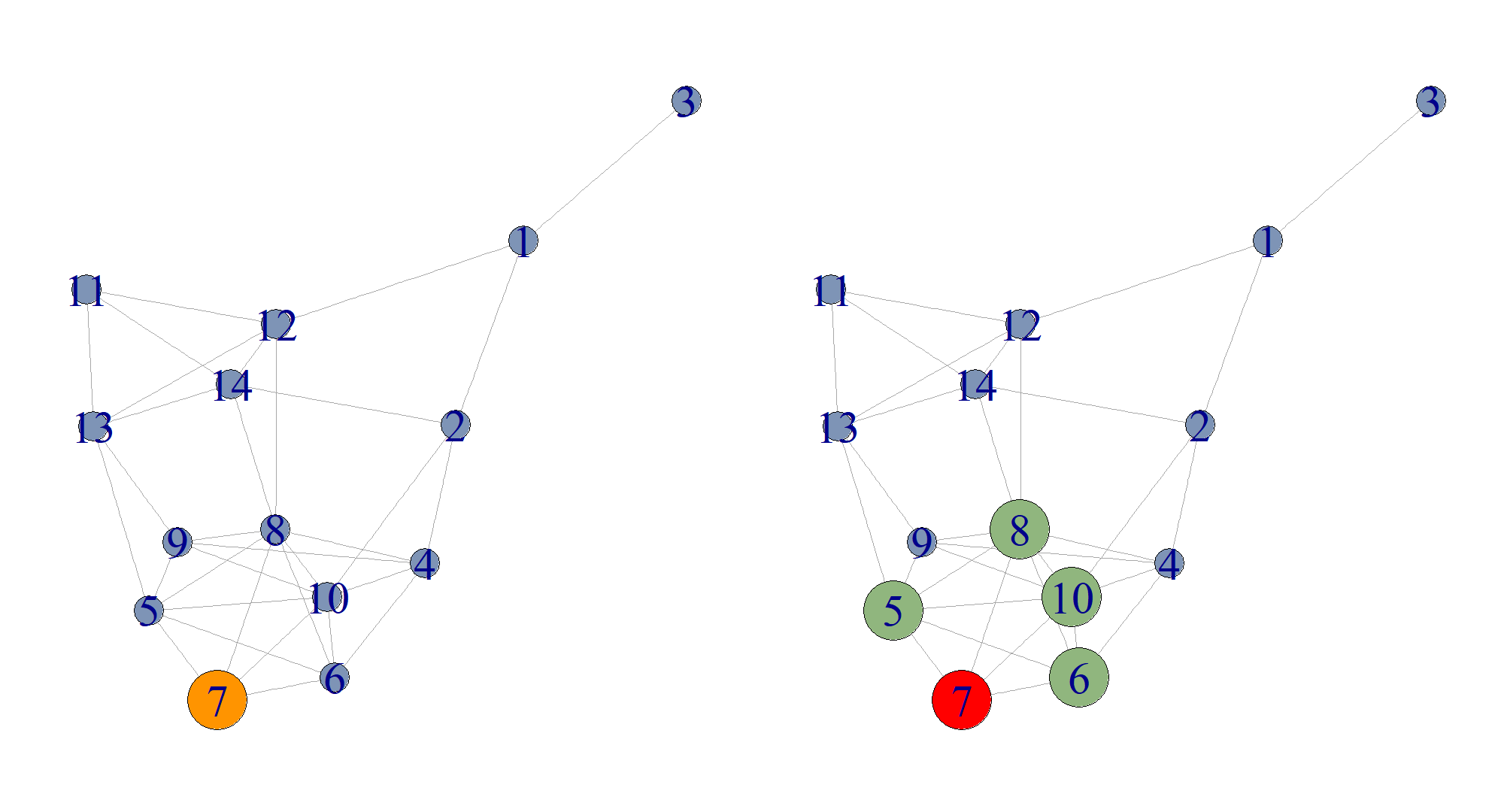
Potenzielle Verbreiter des Beitrags von Person 7 sind in Grün dargestellt
Eine Person, die eine Nachricht erstellt bzw. geteilt hat, ist verbraucht und wird diese Nachricht nicht mehr teilen und erhält die Farbe Rot.
Wie geht es weiter? Von den grün markierten Personen wird ein Anteil, der ungefähr der Wahrscheinlichkeit p entspricht, den Beitrag teilen. Diese Personen sind nun wieder in Orange dargestellt:
Tatsächliche Verbreiter des Beitrags von Person 7 sind in Orange dargestellt
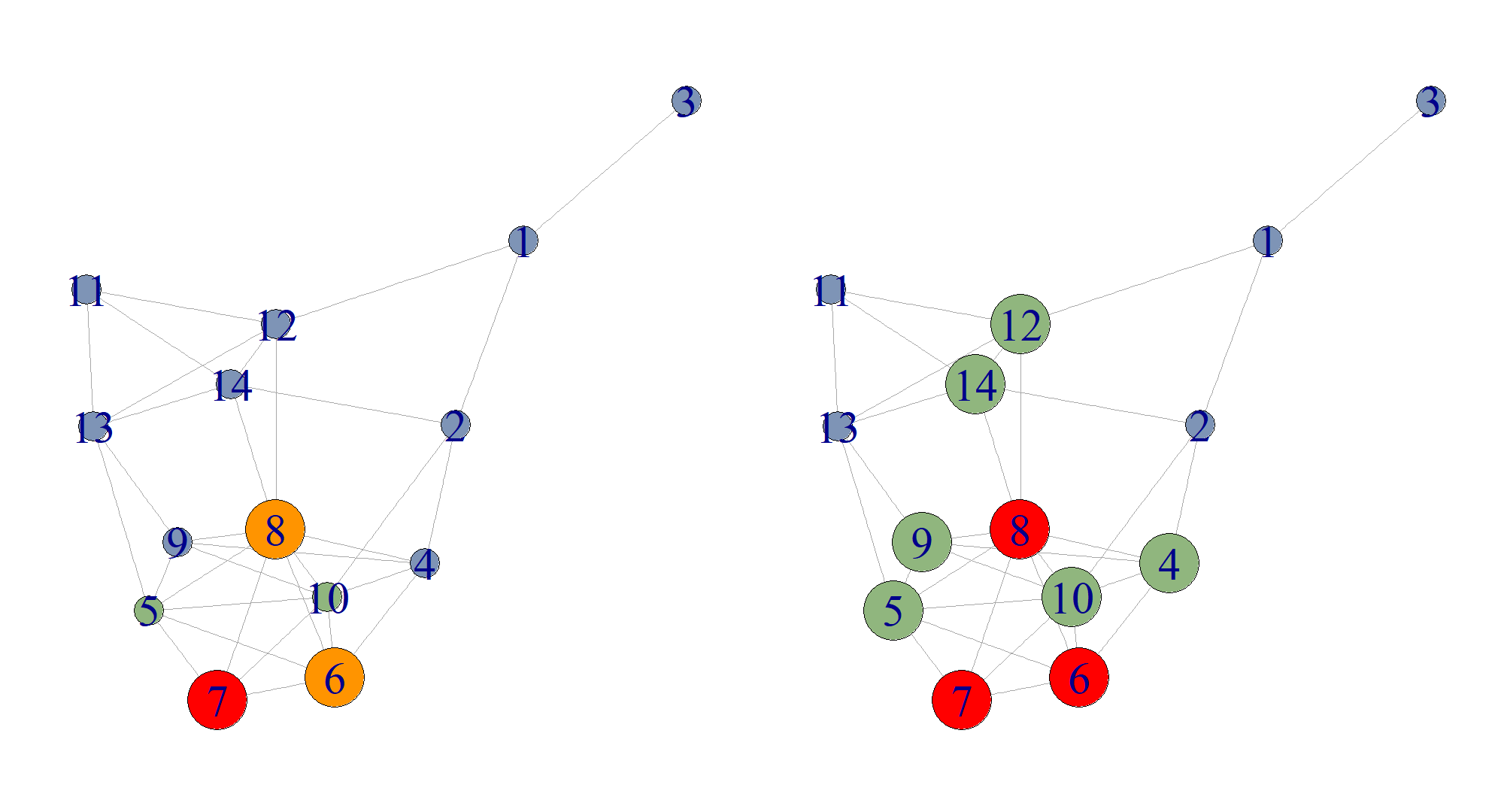
Die Freunde der Teiler werden bestimmt und stellen nun die möglichen Verbreiter der nächsten Runde dar (rechte Seite im obigen Diagramm).
Es ist übrigens zu sehen, dass die Personen 5 und 10 in der zweiten Runde erneut zu den Kandidaten gehören, die den Beitrag verbreiten könnten, obwohl sie dies in der ersten Runde nicht getan hatten. Hier hätte man das Modell alternativ auch so ansetzen können, dass ein einmalig gezeigtes Desinteresse dauerhaft besteht und somit später eintreffende Nachrichten zum gleichen Thema weiterhin ignoriert werden.
Schauen wir dich nun einmal, welchen Einfluss der Parameter p, der die Bereitschaft zur Beitragsteilung beschreibt, auf die Verbreitung einer Nachricht hat. Wir wählen dazu ein etwas größeres Netzwerk.
Das nun in den folgenden Simulationen benutzte Netzwerk haben wir generiert, indem wir zunächst 20 zufällige Mengen mit einer mittleren Anzahl von etwa 10 Personen erzeugt haben. Innerhalb einer Menge wurde die Existenz von verbindenden Kanten zwischen Personen mit hoher Wahrscheinlichkeit angesetzt. Bei zwei Personen aus verschiedenen Mengen existiert eine solche Verbindung nur mit sehr kleiner Wahrscheinlichkeit.
Dermaßen generiert entstehen Cluster, die beispielsweise Cliquen oder Firmen darstellen könnten. Innerhalb der Cluster ist die Vernetzung stark, zwischen den Clustern vergleichsweise schwach ausgeprägt.
Person 1 hat der Welt etwas mitzuteilen
Nun veröffentlicht Person 1 einen Beitrag.
Nehmen wir zunächst an, dass der Beitrag auf eher geringes Interesse stößt, d. h. die Bereitschaft des Teilens sei sehr niedrig angesetzt, z. B. mit einem p = 0.03 (klicken Sie bitte auf die Grafik für eine vergrößerte Darstellung!).
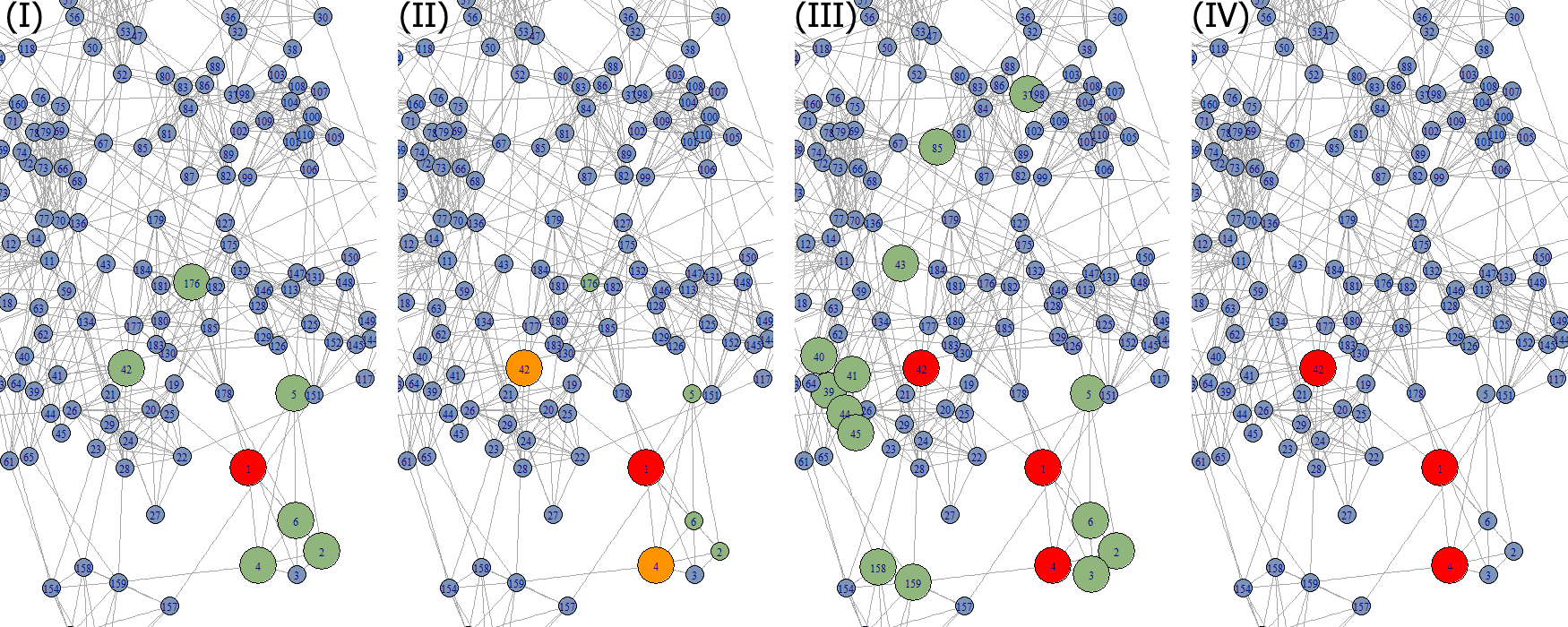
Der Traum ist schnell ausgeträumt!
Teilbild (I) zeigt, dass Person 1 sechs Freunde besitzt, davon 2 außerhalb ihres eigenen Clusters. Vor allem diese beiden Fälle sind die Hoffnungsträger, die für eine weitergehende Verteilung sorgen könnten. Tatsächlich und etwas glücklich teilen sogar zwei der sechs Personen den Artikel (II), trotz der generell geringen Teilungsbereitschaft, wobei sich mit Person 42 vielleicht ein neuer Cluster erschließt. Nun erhalten 14 Personen die Nachricht; von diesen bekommen drei Personen (2, 5 und 6) für die Verbreitung des Beitrags bereits die zweite Chance.
Nichtsdestotrotz und etwas unglücklich ist keine der 14 Personen zur Teilung bereit und somit endet hier bereits der Traum, sehr viele der 185 Personen erreichen zu können.
Das genaue Gegenstück tritt ein, wenn eine Sensationsnachricht an die Freunde verschickt wird, bspw. mit einer Akzeptanz zur Weiterverbreitung von p = 0.99. Betrachten Sie das folgende Video:
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Wenn eine Nachricht so gut wie sicher verbreitet wird, ist bereits nach kurzer Zeit fast jeder informiert. Die Welt ist ja angeblich ein globales Dorf und eine Hypothese lautet, dass jede Person von jeder anderen Person über im Schnitt 6 Freundschaftsbeziehungen erreichbar ist. Für Facebookmitglieder wird sogar behauptet, dass diese Zahl irgendwo zwischen 3 und 4 liegt.
Eine Sensationsnachricht ist also nach kurzer Zeit jedem bekannt und die Aktivitäten verstummen schnell, solange sie nicht künstlich durch Zusatzinformationen am Leben erhalten werden.
Interessanter sind Nachrichten, deren Weiterverbreitungswahrscheinlichkeit nahe einer kritischen Grenze liegt.
Ist die Wahrscheinlichkeit zu klein, sind die Teilungen bald beendet. Ist das p sehr groß, walzt sich die Information ebenfalls innerhalb kürzester Zeit durch das Netzwerk.
Irgendwo dazwischen existiert ein Grenzbereich, sodass zwar nur ein gewisser Prozentsatz der Benachrichtigten zur Teilung des Beitrags bereit ist, aber trotzdem immer genügend viele Freunde verbleiben, die den Informationsfluss am Leben erhalten.
Für das folgende Video haben wir p = 0.25 verwendet:
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Wie man sieht, werden zwar nicht alle Mitglieder des Netzwerkes erreicht, aber die Zeitspanne, in der das Thema irgendwo eine Rolle spielt, ist deutlich größer geworden. Liegt nun ein reales Netzwerk mit Millionen von Mitgliedern vor, kann man sich leicht vorstellen, dass eine Nachricht für gefühlte Ewigkeiten im Netz unterwegs sein kann.
Es existiert ein ganzer Wissenschaftszweig, die Perkolationstheorie, der sich mit der Bildung von zusammenhängenden Clustern (hier der Cluster der Verbreitungswilligen) beschäftigt. Von besonderem Interesse ist dabei die Perkolationsschwelle, also hier die Grenzwahrscheinlichkeit, bei deren Erreichen oder Überschreiten eine positive Wahrscheinlichkeit existiert, dass sich eine Nachricht in einem als unendlich groß angenommenen Netzwerk beliebig lange weiterverbreitet.
Diese Perkolationsschwellen lassen sich nur in Spezialfällen theoretisch ableiten.
Sind bspw. alle Netzwerkteilnehmer wie Perlen auf einer Schnur aufgereiht, sodass eine eintreffende Nachricht von einem Nachbarn nur an den jeweils anderen Nachbarn weitergegeben werden kann, muss die Wahrscheinlichkeit p und damit die Schwelle sogar 1 sein, damit der Nachrichtenfluss mit einer positiven Wahrscheinlichkeit nicht abbricht.
Zum Abschluss seien Personen betrachtet, die auf einem Gitter angeordnet sind und nur Kontakt zu ihren direkten räumlichen Nachbarn haben. Das folgende Video könnte die Verbreitung eines Gerüchts beschreiben:
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Wenn Ihnen der Blog-Beitrag gefallen hat, so teilen Sie ihn doch bitte in einem oder mehreren der unten aufgeführten Netzwerke, damit er so schnell wie möglich viral gehen kann!
Zur Erzeugung der Graphen wurde das igraph-Package verwendet:
Csardi G, Nepusz T: The igraph software package for complex network research, InterJournal, Complex Systems 1695. 2006. http://igraph.org
