Wenn es darum geht, Nachrichten zu verbreiten oder Einfluss auszuüben, ist eine gute Vernetzung stets förderlich. Egal ob wir von Freundschaften in einem sozialen Netzwerk reden oder Links zwischen Webseiten betrachten: Die auftretenden Beziehungen können in einem Graphen dargestellt und analysiert werden.
Beginnen wir doch einmal mit dem World Wide Web, dessen phänomenaler Erfolg sicherlich zum Großteil der Möglichkeit zu verdanken ist, Hyperlinks auf andere Webseiten setzen zu können.
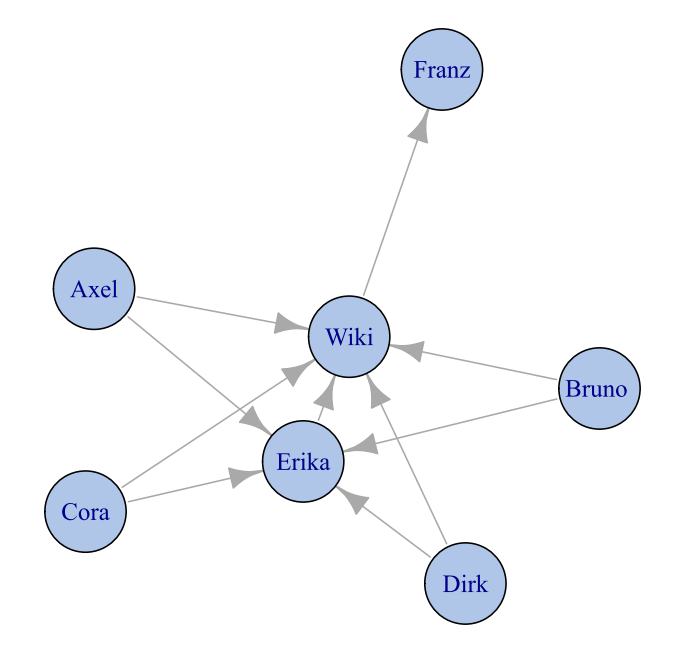
In unserem Beispiel sei ein spezielles Fachgebiet betrachtet. Hier gibt es eine Expertin Erika, deren Webseite von den vier Amateuren Axel, Bruno, Cora und Dirk gern gelesen wird und deshalb verlinkt wurde. Die gleiche Ehre gebührt dem Wikipediaeintrag, der zusätzlich auch noch von Erikas Seite aus erreichbar ist. Die Wikipedia-Seite hingegen verweist auf die Seite von Franz. Die folgende Abbildung – es handelt sich hier um einen sogenannten gerichteten Graphen – zeigt die entstandenen Beziehungen zwischen den Webseiten:
Wer verweist auf wen?
Wer ist in diesem Netzwerk besonders wichtig?
Gäbe es nur ehrliche und rechtschaffene Webbürger, könnte ein erster Ansatz sein, die Wichtigkeit in der Zahl der eingehenden Verbindungen zu sehen. Je mehr Links auf eine Seite zeigen, desto interessanter sollte der Inhalt sein. Definieren wir also Wichtigkeit beispielsweise über die Anzahl eingehender Links, wird hier die Wikipedia-Seite mit fünf eingehenden Links zur wichtigsten Seite erklärt, dicht gefolgt von Erika mit ihren vier Links:
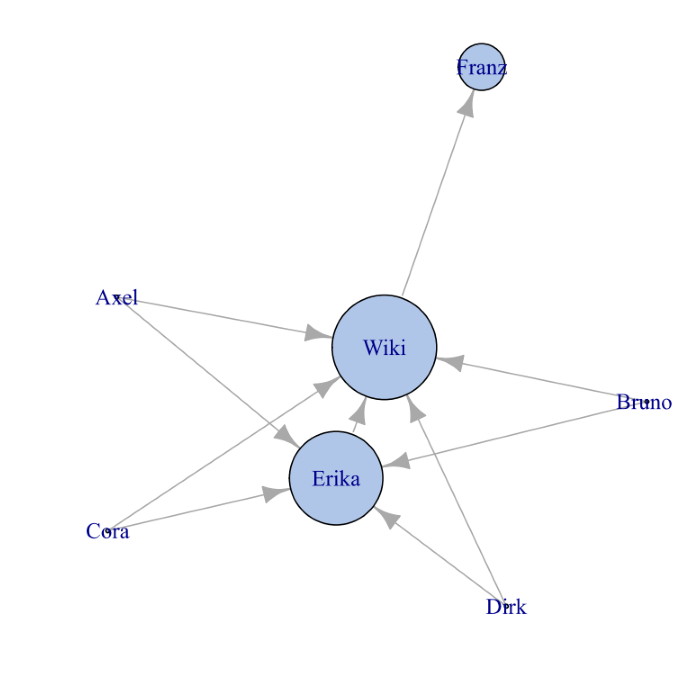
Wichtigkeit durch viele eingehende Links
Linkfarmen unterlaufen nun diesen schönen Ansatz und dienen nur dazu, auf vielen künstlichen Seiten Links auf ausgewählte, zu pushende Webseiten zu erzeugen, um deren angebliche Wichtigkeit zu erhöhen.
Eine Inkonsistenz stört darüber hinaus: Wenn die vier Fans von Erika unwichtig sind, da sie selbst ja keine eingehenden Verlinkungen aufweisen können, wieso kann dann Erika wichtig sein, da sie sich ja nur auf die Hyperlinks von diesen “unwichtigen” Personen berufen kann? Wenn aber auch Erika keine Bedeutung besitzt, dann gilt dies ebenso für die Wikipediaseite und für Franz – letztendlich wären dann alle Seiten unwichtig.
Aus diesen Gründen sollte ein stabileres Maß hergenommen werden, das jedem Knoten eine Wichtigkeit zuordnet und trotzdem in sich konsistent ist.
Von den Google-Gründern Larry Page und Sergei Brin stammt der passend benannte PageRank-Algorithmus, der versucht, diesen Anforderungen Rechnung zu tragen. Es gibt eine Random-Surfer-Interpretation des Ansatzes: Angenommen, eine Person wird auf einer beliebigen Seite ausgesetzt und bewegt sich dann mit gleichen Wahrscheinlichkeiten zu einem der jeweils vorhandenen ausgehenden Links, dann ist die zugewiesene Wichtigkeit des Knotens gleich der Wahrscheinlichkeit, eine Person nach einer Weile des Surfens auf der zugehörigen Seite anzutreffen.
Es muss noch eine Erweiterung geben, damit immer eine vernünftige Lösung existiert: Da in die Knoten von Axel, Bruno, Cora und Dirk keine Links eingehen, gäbe es erst einmal keine Möglichkeit, auf diesen Seiten über Hyperlinks zu landen. Deshalb wird angenommen, dass der Surfer von jedem Knoten aus mit einer kleinen Wahrscheinlichkeit zu einem beliebigen Knoten teleportiert werden kann und somit auch diese vier Knoten erreichbar sind und damit tatsächlich eine positive Wichtigkeit erhalten.
Ebenso stellt Franz eine Sackgasse dar, da er auf keine anderen Seiten verlinkt. In einem solchen Fall wird dann ebenfalls zufällig zu einem der insgesamt 7 Knoten gesprungen – der Sprung könnte also auch wieder bei Franz selbst landen.
Der PageRank-Algorithmus ermittelt somit die generelle Relevanz einer Webseite allein aus der Verlinkungsstruktur. Diese Relevanz kann dann bei Suchergebnissen nach Wörtern bei der Anordnung der Ergebnisse mitberücksichtigt werden.
Bei Verwendung des PageRank-Algorithmus ergeben sich für unser Beispiel-Netzwerk die folgenden Wichtigkeiten:
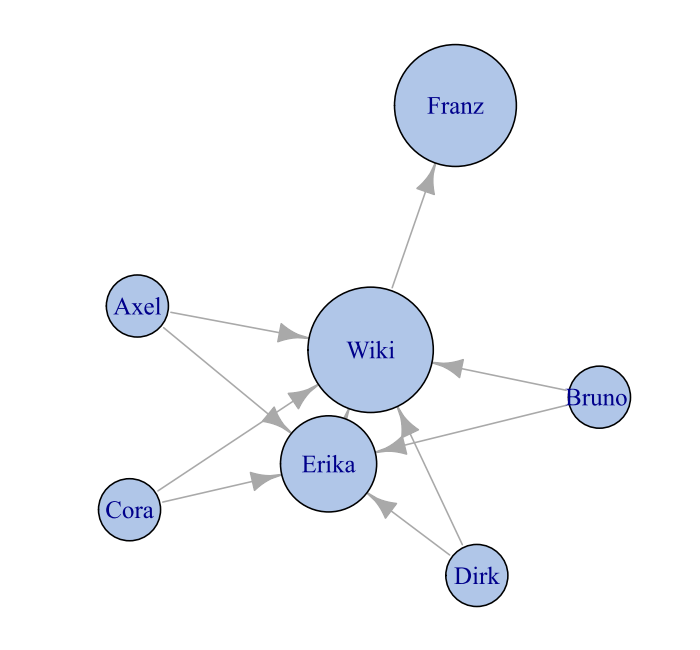
Wichtigkeit nach PageRank-Algorithmus
Da Franz im Falle der Nutzung des einzigen ausgehenden Links das gesamte Gewicht der Wikipediaseite erhält, ist nun seine Wichtigkeit etwa in der Größenordnung der Wikipediaseite selbst anzusiedeln. Die eigene Wichtigkeit ist somit hoch, wenn entweder viele unbedeutende oder wenige bedeutende Webseiten auf die eigene Seite verweisen.
Noch besser sind natürlich viele bedeutende Seiten, die auf uns verlinken.
Am Ende dieses Blogbeitrags gibt es noch eine animierte Visualisierung des PageRank-Algortihmus, aber schauen wir nun erst einmal auf einen anderen Anwendungsbereich: Bei sozialen Netzwerken wie LinkedIn, Xing oder Facebook bestehen Verbindungen oder “Freundschaften” zwischen den Personen. Veröffentlichte Beiträge erscheinen bei den Verbindungen und können geteilt werden.
Kann man aus der Netzwerkstruktur, die natürlich erst einmal nur dem Betreiber des sozialen Netzwerks in ihrer Vollständigkeit bekannt ist, die Bedeutung von Personen für die Weitergabe von Nachrichten oder den generellen Einfluss eines Teilnehmers ablesen?
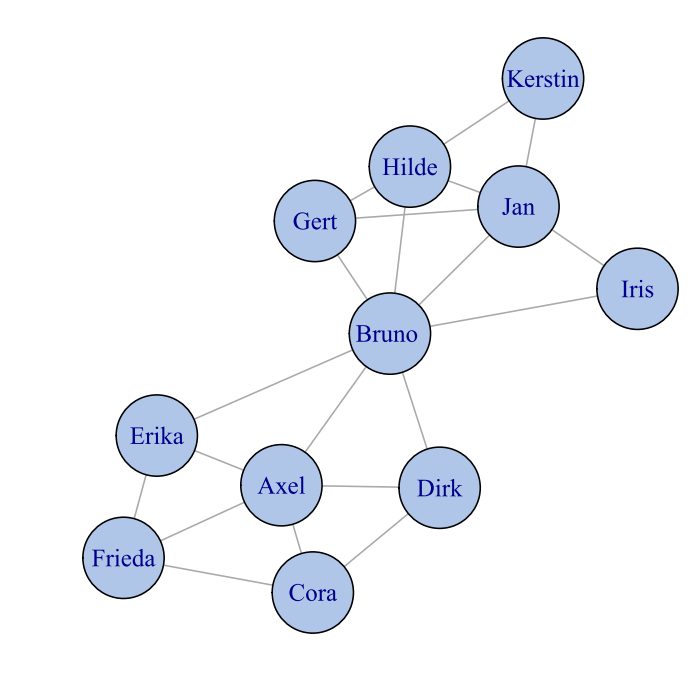
Betrachten wir dazu die folgende Struktur, die die Freundschaften zwischen elf Personen abbildet. Hier handelt es sich übrigens um einen ungerichteten Graphen, da die Freundschaft keine bestimmte Richtung aufweist (die gäbe es bei einer einseitigen Beziehung, bei der wir einer Person folgen, diese aber uns nicht!):
Freundschaften
Es existieren nun eine Reihe von Kennzahlen, die versuchen, bestimmte Eigenschaften des Netzwerks berechenbar zu machen.
Beispielsweise drückt die Kantendichte (edge density) aus, welcher Anteil von möglichen Freundschaften tatsächlich realisiert ist. In kleinen Netzwerken sollten tendenziell höhere Werte anzutreffen sein. In unserem Beispiel liegt ein Wert von 0.36 vor. Im Extremfall kann dieser Wert 1 sein, wenn jede Person mit jeder Person befreundet ist.
Ein hoher Wert deutet bspw. auf kurze Wege hin, die Nachrichten zur Verbreitung brauchen.
Ein einfaches Maß für die Bedeutung ist der Grad (node degree) eines Knotens: Er zählt einfach die Kontakte einer Person. Hiernach ist Bruno die wichtigste Person, allein aufgrund der Anzahl der direkten Verbindungen:
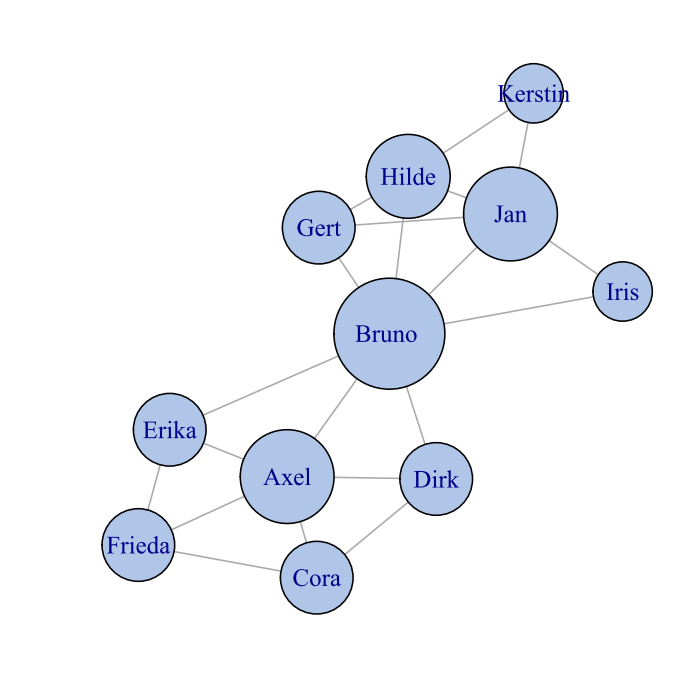
Bruno kennt die meisten Leute!
Bruno ist aber auch noch aus einem anderen Grunde wichtig: Alle Nachrichten, die aus dem unteren Bereich in den oberen gelangen sollen, werden zwangsläufig von Bruno kontrolliert. Hierfür gibt es das Maß der Zwischenzentralität (betweenness centrality).
In einer von mehreren möglichen Definitionen werden kürzeste Wege zwischen jedem Paar von Personen untersucht. Beispielsweise gibt es mehrere kürzeste Wege der Länge 4, um von Cora aus Kerstin zu erreichen. Ein möglicher kürzester Weg lautet Cora – Axel – Bruno – Jan – Kerstin, ein anderer ist Cora – Dirk – Bruno – Hilde – Kerstin.
Personen, die nun häufiger auf solchen kürzesten Wegen liegen (wie etwa Bruno) erhalten einen hohen Wert. Im Gegensatz sind beispielsweise Iris, Kerstin und Gert für Verbreitung von Nachrichten und Gerüchten nicht ganz so wichtig, da Jan und Bruno, bzw. Jan und Hilde, als auch Hilde und Bruno auf direktem Wege verbunden sind. Werden die Flächen proportional zur Zwischenzentralität angesetzt, ergibt sich der folgende Graph:
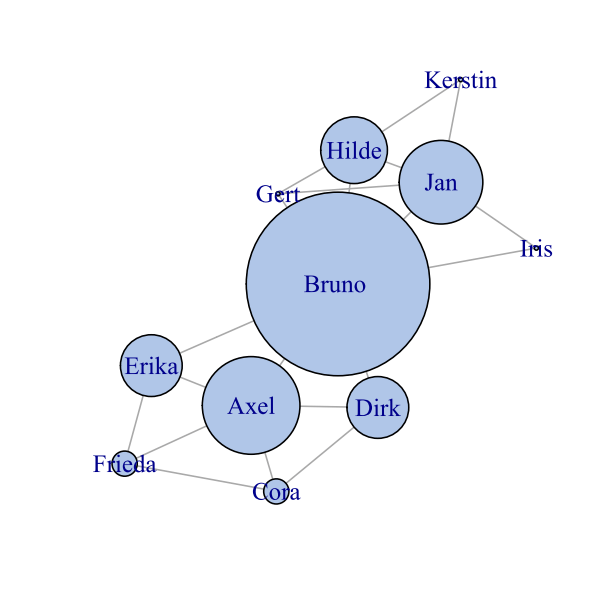
Bruno verbindet oder trennt zwei Welten!
Es wird mehr als deutlich, dass die Machtposition in diesem Netz von Bruno eingenommen wird. Gibt es zwischen zwei Personen eine direkte Verbindung, kann diese logischerweise durch keine andere Person blockiert werden – gute Freunde kann niemand trennen!
Letztendlich gibt es auch ein Clusterverfahren, das Gemeinschaften erkennen kann und auf der Zwischenzentralität aufbaut:
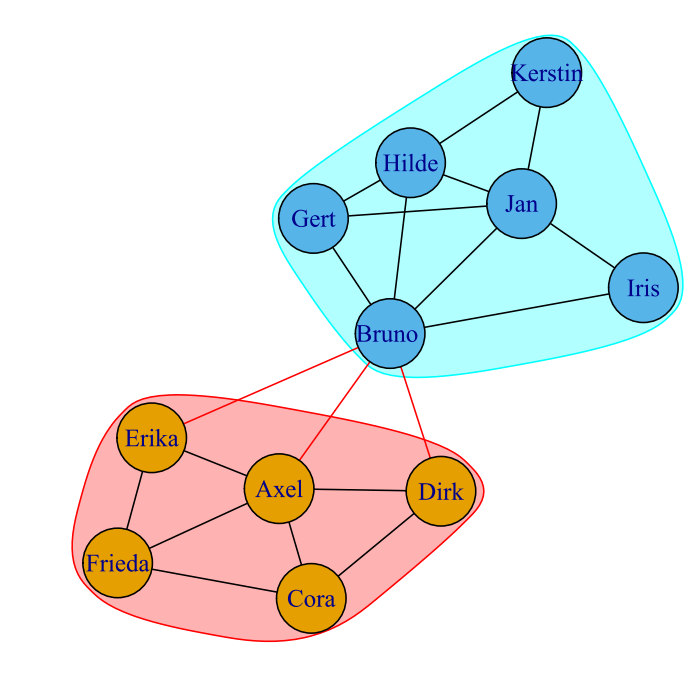
Zwei Gruppen mit Bruno als Kontaktmann
Hier erwies sich eine Aufteilung in zwei Cluster als optimal.
Besonders interessant wird es, wenn die Ausbreitung einer Nachricht verfolgt wird. Leider sind solche Informationen für außenstehende Nutzer kaum einzusehen.
Damit eine Nachricht viral werden kann, muss das vorhandene Netzwerk stimmen, also eine große Reichweite erst einmal prinzipiell möglich sein. Es hilft nichts, viele Freunde zu besitzen, wenn diese ihrerseits schlecht vernetzt sind und eine Botschaft sofort versandet. Zusätzlich muss dann auch die Bereitschaft vorhanden sein, das Empfangene zu teilen.
Jetzt befinden wir uns aber schon auf dem Gebiet der Perkolationstheorie, die interessant genug ist für einen eigenen Blogbeitrag!
Zum Abschluss noch das versprochene kleine Schmankerl:
Unsere Netzwerkanhänger betreiben natürlich auch Webseiten und haben sich bei vorhandener Sympathie jeweils gegenseitig verlinkt. Das folgende Video verdeutlicht die Idee des PageRank-Algorithmus.
Der Zufallssurfer startet hier auf Axels Seite und besucht entweder einen der Nachbarn (orange) oder teleportiert sich zufällig zu einer der elf Seiten (rot). Im Bar-Chart rechts wird mitgezählt, wie häufig die jeweiligen Seiten besichtigt wurden und die Größe der Knotenkreisflächen ist proportional zur Anzahl (und wird im Video so skaliert, dass die größte Fläche der 11 Knoten unverändert bleibt!).
Mit dem Laden des Videos akzeptieren Sie die Datenschutzerklärung von YouTube.
Mehr erfahren
Die relativen Häufigkeiten streben dann gegen die Werte, die für die Bedeutung der Knoten beim PageRank-Algorithmus ermittelt werden. Das Endergebnis nach 1000 Surfschritten sieht dann folgendermaßen aus und wieder wird deutlich, dass (B)runo auch beim PageRank die Nase vorn hat:
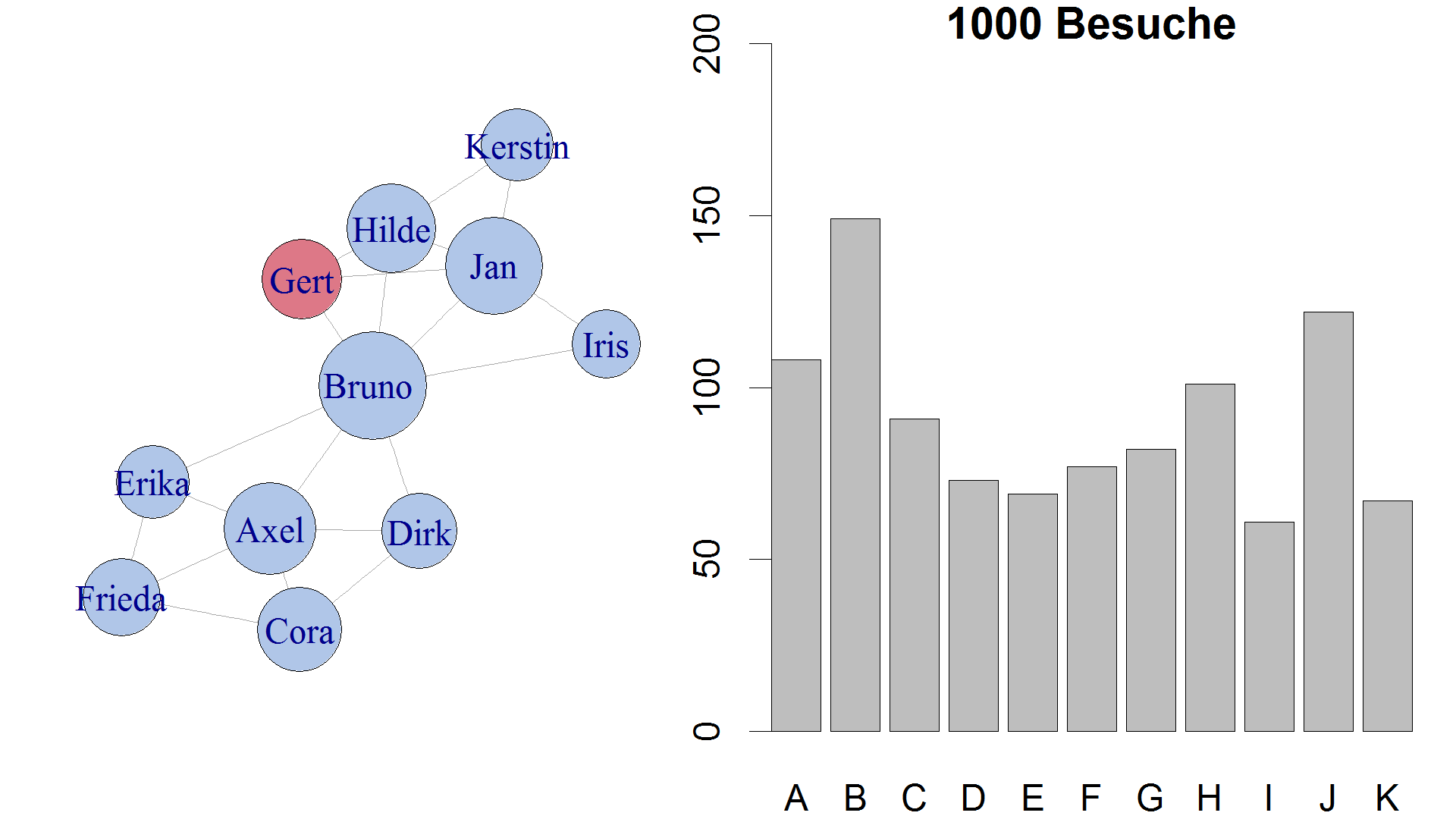
Das Endergebnis nach 1000 Schritten
Zur Erzeugung der Graphen und Berechnung der Kennzahlen wurde das igraph-Package verwendet:
Csardi G, Nepusz T: The igraph software package for complex network research, InterJournal, Complex Systems 1695. 2006. http://igraph.org
