Werden hochwertige Gebrauchsgüter oder Maschinen verkauft, erwartet der Kunde Angaben zur mutmaßlichen Lebensdauer. Im laufenden Betrieb ist jedoch bei der Interpretation der Angaben Vorsicht geboten, um nicht die falschen Schlüsse zu ziehen!
Im Beitrag Keine Angst vor Faltungen hatten wir uns bereits mit der Lebensdauer von Maschinenteilen beschäftigt. Dort stand jedoch eher die Frage im Mittelpunkt, wie lange wohl ein großer Vorrat von relativ schnelllebigen Verbrauchsgütern halten wird.
Nun betrachten wir Geräte, die üblicherweise länger in Betrieb sind. Beispielsweise sei die Lebensdauerverteilung einer durchgehend betriebenen Maschine durch die folgenden Werte gegeben:

Lebensdauerverteilung (Angabe in vollendeten Jahren)
Bei Geräten, die im Laufe eines Jahres einen Defekt erleiden, gehen bei uns nur die vollständig absolvierten Jahre in die Berechnung der Lebensdauer ein. Wir haben somit die Lebensdauer diskretisiert – in diesem Falle auch, um eine einfachere Darstellung mittels Pivottabellen zu ermöglichen.
Ungeachtet der Tatsache, dass hier wohl ein Qualitätsproblem vorliegt, da eine Maschine mit 30-prozentiger Wahrscheinlichkeit das erste Jahr nicht überlebt, suchen wir nun nach einfachen Kennzahlen, die es dem Kunden ermöglichen, die Lebensdauer besser einschätzen können.
Die einfachste Größe ist durch die erwartete Lebensdauer gegeben, also die Lebensdauer, die sich im Mittel bei sehr vielen baugleichen Geräten ergeben wird. Jede mögliche Lebensdauer wird mit ihrer Wahrscheinlichkeit gewichtet und die entstehenden Terme werden aufaddiert. Die folgende Tabelle zeigt die Berechnung mit dem Ergebnis:
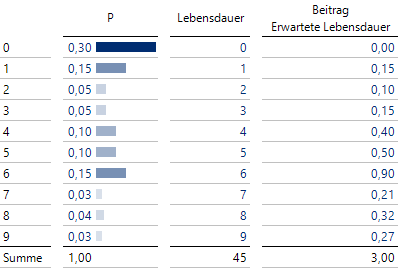
Berechnung der erwarteten Lebensdauer
Hier in diesem Beispiel beträgt die erwartete Lebensdauer exakt 3 Jahre.
Was passiert, wenn jemand eine solche Maschine erworben hat und zu den Glücklichen gehört, die das verflixte erste Jahr schadlos überstanden haben? Kann er nun auf zwei weitere sorglose Jahre des reibungslosen Betriebs hoffen? Wie ändert sich also unter der Annahme “Erstes Jahr schadlos überstanden” die Erwartung?
Dazu müssen Wahrscheinlichkeiten eben unter dieser Annahme berechnet werden: Wird die Wahrscheinlichkeit für den Fall Lebensdauer = 0 gestrichen, der ja nun nicht mehr auftreten kann, ergibt die Summe der übrigen Wahrscheinlichkeiten P_vorläufig1 0.7.
Dies entspricht genau der Wahrscheinlichkeit, das erste Jahr unbeschadet zu überstehen. Um wieder eine korrekte Wahrscheinlichkeitsverteilung mit einer Summe von 1 zu erhalten, müssen alle vorläufigen Wahrscheinlichkeiten durch 0.7 dividiert werden, um die bedingten Wahrscheinlichkeiten P_Update1 zu erhalten:
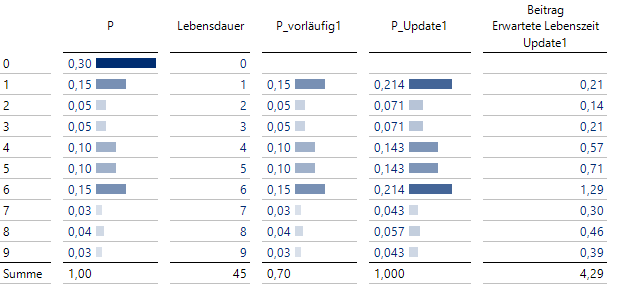
Update der erwarteten Lebensdauer nach 1 Jahr
Mit diesen Wahrscheinlichkeiten P_Update1 wird die Erwartung nun zu 4.29 berechnet. Da bereits 1 Jahr verstrichen ist, heißt das, dass die nun verbleibende erwartete Restlebensdauer von 4.29 – 1 = 3.29 zum einen deutlich größer als die oben fälschlicherweise vermuteten 2 Jahre und zum anderen sogar größer als die ursprünglich zu erwartende Gesamtlebensdauer von 3 Jahren ist.
Man kann übrigens zeigen, dass die erwartete Gesamtlebensdauer nach jedem verstrichenen Jahr ohne Ausfall, in dem aber ein Ausfall hätte passieren können, steigen muss.
Eine höhere Ausfallwahrscheinlichkeit zu Beginn ist nicht zwingend untypisch und deutet unter Umständen auf einen schwierigen Produktionsprozess hin, bei dem sich nicht unmittelbar erkennbare Schwachstellen ergeben können, die sich erst nach einer gewissen kurzen Zeit der Nutzung bemerkbar machen. Um das Auftreten solcher Enttäuschungen beim Kunden zu vermeiden, wird häufig Burn-in betrieben, d. h. die Maschinen laufen bereits eine gewisse Zeit beim Hersteller, um die Wackelkandidaten auszufiltern.
Auch bei unserem Beispiel wäre es somit zumindest in der Theorie überlegenswert, Burn-in in Betracht zu ziehen, da ja eine 1 Jahr alte, bis dahin fehlerfrei gelaufene Maschine im Schnitt noch länger hält als ein brandneues Gerät.
Wenn bereits exakt 3 Jahre ohne Schaden verstrichen sind, sieht die passende Tabelle folgendermaßen aus:
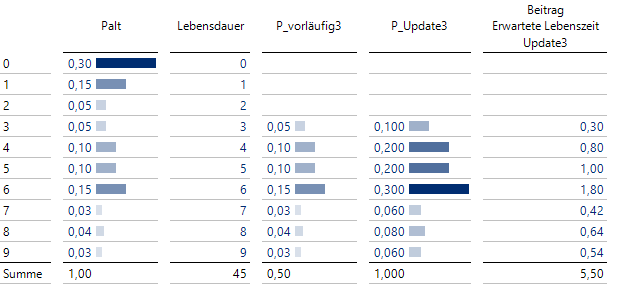
Update der erwarteten Lebensdauer nach 3 Jahren
Hier wird wiederum deutlich, dass sich nach 3 Jahren ohne Schaden erneut die nun zu erwartende Gesamtlebensdauer erhöht, die jetzt 5.5 Jahre beträgt.
Der Kunde sollte nun vor allem nicht glauben, dass im laufenden Jahr der Fluch in Gestalt der ursprünglichen Erwartung von 3 Jahren zuschlagen wird. Die Wahrscheinlichkeit, dass das Gerät vor Vollendung des vierten Jahres den Geist aufgibt, beträgt inzwischen nur noch 10 %, im Gegensatz zu den 55 %, die bei Inbetriebnahme der Maschine galten.
Neben der Erwartung kann somit auch die Angabe einer Wahrscheinlichkeit, dass ein bestimmter Threshold übertroffen wird, nützlich sein. Auch diese Werte verändern sich mit jedem bereits absolvierten Jahr. Beispielsweise lassen sich jedes Jahr Wahrscheinlichkeiten aktualisieren, dass die Maschine mindestens 3 Jahre halten wird:
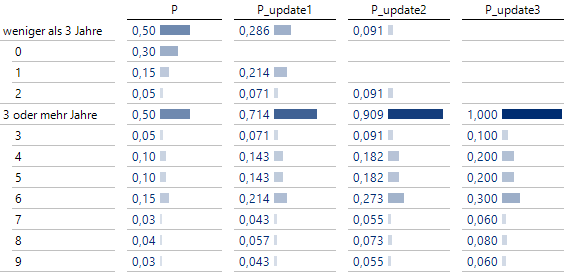
Hält die Maschine mindestens 3 Jahre?
Steht es zu Beginn fifty-fifty, steigt nach einem absolvierten Jahr die Wahrscheinlichkeit auf 71 %, nach 2 Jahren sind es bereits 91 % und bei 3 oder mehr Jahren ist die Bedingung logischerweise immer erfüllt.
Nehmen wir etwa an, dass die Ingenieure unserer Maschine ob der hohen Ausfallwahrscheinlichkeit im ersten Jahr nicht ruhen konnten und vor drei Jahren ein verbessertes Nachfolgemodell präsentiert haben, für das jedoch noch keine Langzeitprognosen vorliegen.
Das Modell hat sich gut verkauft und immerhin können wir die Anteile für Lebensdauern von 0 bis 2 Jahren mit hoher Genauigkeit benennen:
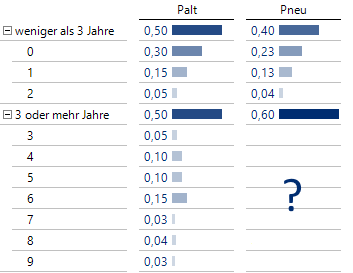
Gesicherte Daten für das neue Modell
Da der Rest der Maschinen noch in Betrieb ist, weiß man immerhin schon, dass eine Maschine mit einer Wahrscheinlichkeit von 60 % mindestens volle drei Jahre halten wird (eigentlich liegen hier relative Häufigkeiten vor, bei denen wir aber eine große Grundgesamtheit annehmen, sodass die Werte schon stabil sind).
Die exakte Lebensdauer dieser noch im Betrieb befindlichen Maschinen ist noch ungewiss – es handelt sich hierbei um sogenannte zensierte Daten, denen wir lieber einen eigenen, ausführlichen Blogbeitrag widmen sollten.
Die Frage ist deshalb nun, wie sich die 60 % auf die Jahre 3, 4, 5,… aufteilen, damit wir beispielsweise die erwartete Lebensdauer ausrechnen können. Ohne zusätzliche Annahmen geht es hier nicht weiter.
Wir werfen einen Blick auf Survivalfunktion und die Ausfallrate, weitere Größen, die möglicherweise nützlich sein können.
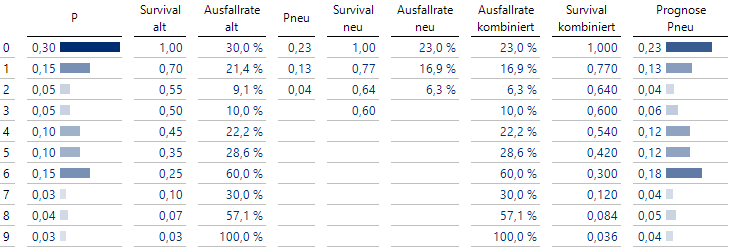
Herleitung einer Lebensdauerverteilung für das neue Modell
Kleine Randbemerkung: Alle in diesem Blogbeitrag benötigten Berechnungen erfolgten zur Gänze in DeltaMaster!
Die Ausfallrate gibt die Wahrscheinlichkeit an, dass die Maschine im laufenden Jahr ausfällt, gegeben dass sie seit Beginn des Betriebs bis zum Anfang des Jahres reibungslos lief. Die Wahrscheinlichkeit, dass die Maschine mindestens bis zum Anfang eines Jahres t fehlerfrei lief, nennt man auch Survival-Funktion S(t).
Der Wert S(t) für das Jahr t lässt sich einfach berechnen – dazu wird von 1 die Summe der Ausfallwahrscheinlichkeiten P der Vorperioden abgezogen. Zum Beispiel ergibt sich der Wert S(2) im Jahr 2 als 1 – 0.3 – 0.15 = 0.55.
Die Ausfallrate ist nun einfach der Quotient aus P(t) und S(t) und zeigt somit an, wie viel Prozent der am Anfang eines Jahres noch funktionierenden Maschinen im Laufe dieses Jahres ausfallen.
Für das neue Modell sind nun diese Werte nur am Anfang bekannt. Um Vorhersagen für spätere Jahre zu erhalten, kann man beispielsweise parametrische Modelle für die Lebensdauerverteilung, die Survivalfunktion oder eben für die Ausfallrate anpassen.
Ist eine dieser Funktionen gegeben, lassen sich die jeweils anderen beiden daraus ableiten.
Wir versuchen hier eine einfache pragmatische Lösung, die der Kategorie “konservativ optimistisch” zuzuordnen ist. Dazu übernehmen wir die Ausfallraten des neuen Modells, soweit bekannt. Ansonsten belassen wir es bei den Ausfallraten des alten Modells (optimistische Annahme: “Das neue Modell verhält sich bei den unbekannten Werten zu keinem Zeitpunkt schlechter …”, konservative Ergänzung: “… aber auch nicht besser!”).
Hieraus lassen sich die kombinierten Ausfallraten und Survivalfunktionen berechnen und aus diesen auch wieder die Lebensdauerverteilung (siehe letzte Spalte) rekonstruieren.
Übrigens hätten sich identische Resultate ergeben, wenn die Wahrscheinlichkeiten des alten Modells für Lebensdauern >= 3 proportional gestreckt worden wären, sodass die Summe anstatt 0.5 wie vorher nun 0.6 wie beim neuen Modell ergeben hätte.
Schaut man sich die Survivalfunktion des alten Modells (schwarz) und den bekannten Ausschnitt für das neue Modell an (durchgezogener roter Linienzug), so zeigt die gestrichelte rote Funktion unsere Schätzung der fehlenden Teile der neuen Funktion an.
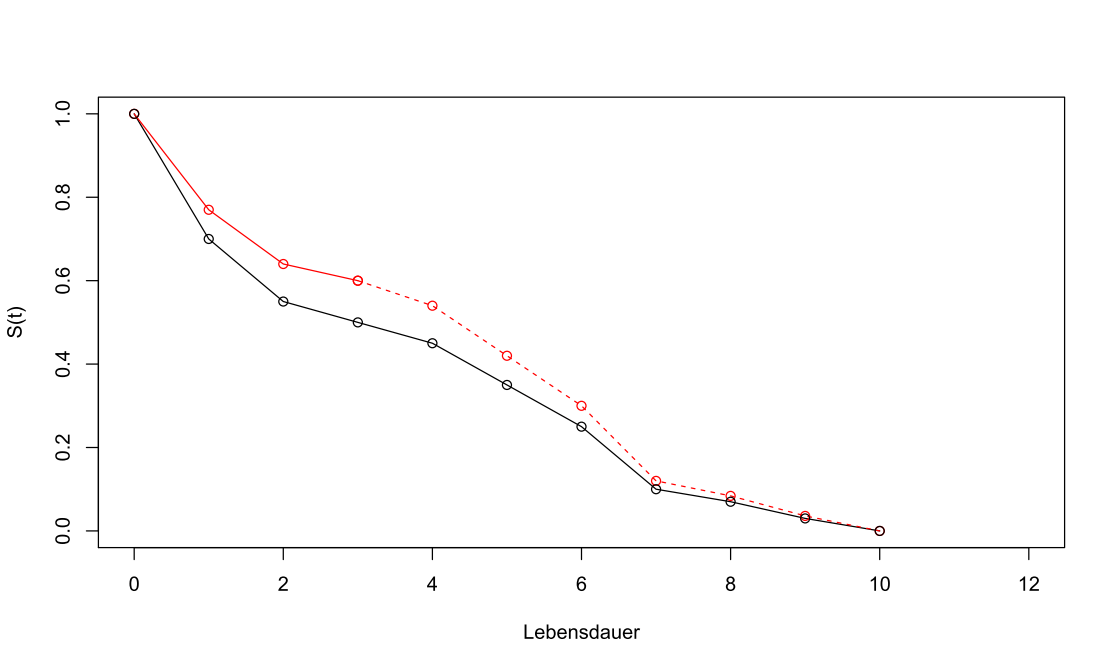
Geschätzte Survivalfunktion des neuen Modells (rot)
Jetzt lässt sich die erwartete Lebensdauer des neuen Modells schätzen, die nun ca. 4.5 anstelle der 3 Jahre des alten Modells beträgt.
Bei den genannten Annahmen wird das neue Modell aber weiterhin nicht die maximalen 9 Jahre des alten Modells überstehen. Ein parametrisches Modell könnte sich hier anders verhalten, aber zur Festlegung einer bestimmten parametrischen Modellfamilie bietet das hier bisher nur einzige komplett vorliegende Modell relativ wenige Anhaltspunkte.
