Wenn ein Klassifikator gesucht wird, muss der Anwender oft Abstriche bei der Performanz in Kauf nehmen, falls eine leichte Interpretierbarkeit des Modells gewünscht ist. Es gibt aber eine verblüffend gut funktionierende Methode, der Güte der Prognose auf die Sprünge zu helfen!

In unserem Szenario, das für Projekte aus dem Bereich Predictive Analytics typisch ist, lautet die Aufgabe, Objekte aufgrund ihrer Eigenschaften einer von zwei Klassen zuzuweisen. Uns stehen etliche Beispiele zur Verfügung, bei denen die Klasse (“Rot” oder “Grün”) bekannt ist. Im verwendeten Beispiel sieht die Datenlage folgendermaßen aus:

Die Ausgangslage

Anwendungen aus der Praxis haben natürlich meistens viel mehr als diese zwei Inputs, die wir hier der Anschaulichkeit halber verwenden. Außerdem kann es Überlappungen der Klassen geben. Man sollte sich also vorstellen, dass üblicherweise der Zusammenhang zwischen Inputs und Klasse nicht so leicht und eindeutig zu erkennen ist wie in diesem Beispiel.

Die verantwortliche Person verwendet einen Entscheidungsbaum als Klassifikator. Damit dieser leicht interpretierbar bleibt, ist die Tiefe des Baumes, also die maximale Anzahl von aufeinanderfolgenden Fragen auf 2 beschränkt:

Der angepasste Entscheidungsbaum

In jeder Abfrage wird nur nach einem der beiden Inputs gefragt. Als Ergebnis wird der Inputraum in Flächen eingeteilt, die durch waagerechte und senkrechte Geraden getrennt werden. Da die Tiefe des Baumes auf 2 beschränkt ist, können maximal 4 solcher Flächen auftreten, die dann der jeweils vorherrschenden Klasse zugeordnet werden. Die vorhergesagten Klassen für jeden der Bereiche – in unserem Beispiel sind es 3 – sind in der folgenden Grafik visualisiert:

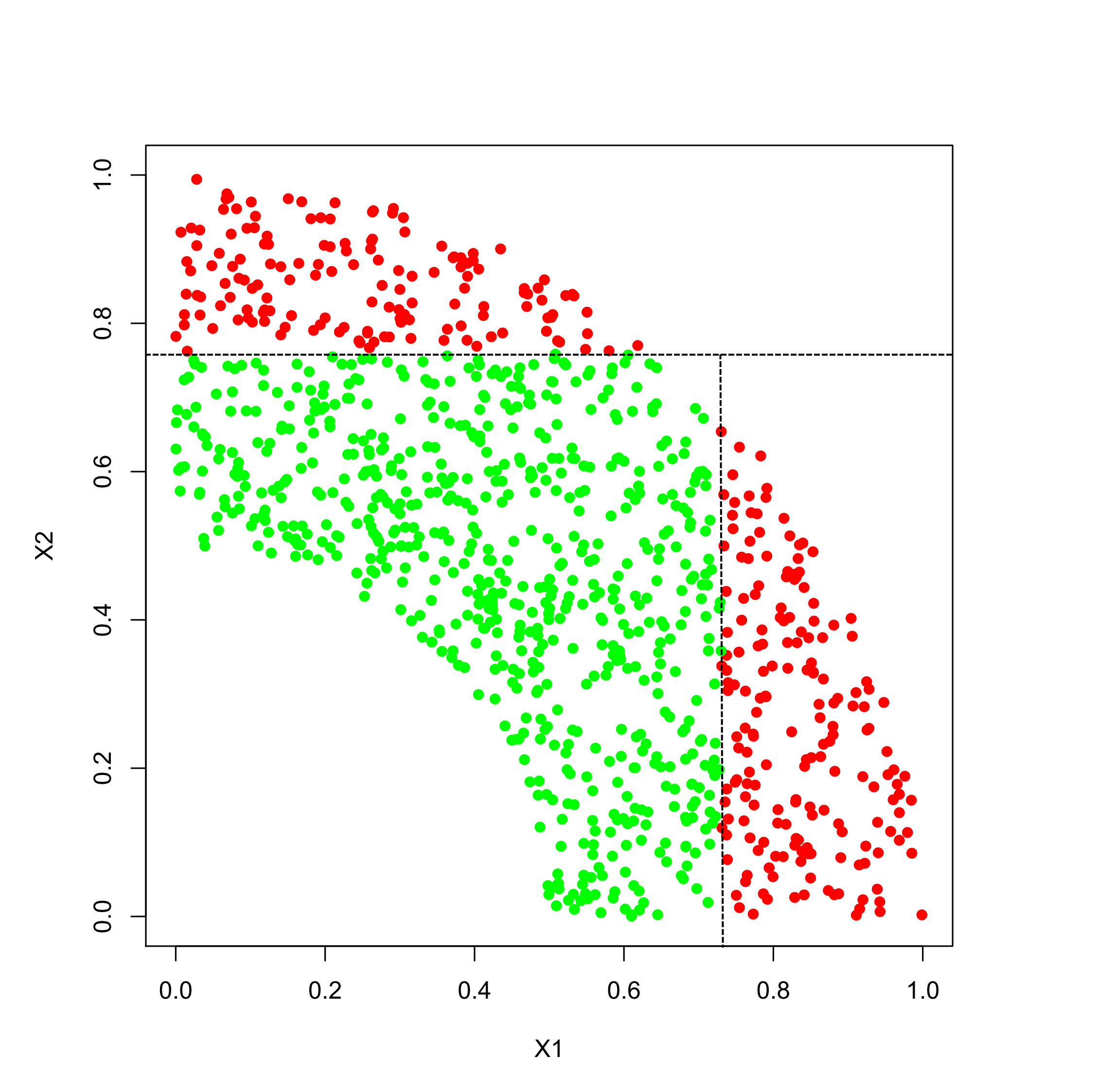Vorhersagen des angepassten Entscheidungsbaums

Ein solcher Entscheidungsbaum ist leicht interpretierbar. Angenommen, X1 sei ein Längengrad und X2 bezeichne die Breite, dann kann die Klassifikationsvorschrift kurz beschrieben werden:

• Alle Fälle nördlich von 0.76 sind “Rote”
• Fälle südlich von 0.76 sind “Rote”, falls sie östlich von 0.73 liegen
• Fälle südlich von 0.76 sind “Grüne”, falls sie westlich von 0.73 liegen

So einfach die Vorschriften auch sind, sie haben einen gravierenden Nachteil: Etwa 16 % der Fälle werden mit diesen Regeln fehlklassifiziert. Die falsch zugewiesenen Fälle sind in der folgenden Grafik markiert:

Störende Fehlzuweisungen

Es existiert nun ein geniales Meta-Verfahren, Boosting genannt, das mit der vorhandenen Datenmasse sehr clever und ökonomisch umgeht. Die Idee ist, die zur Verfügung stehenden Daten wiederholt mit unterschiedlicher Gewichtung der einzelnen Datensätze zu verwenden, jeweils das einfache Verfahren, also hier den Entscheidungsbaum anzuwenden und dann aus den Einzelvorhersagen eine Gesamtvorhersage zu erzeugen.

Eine Möglichkeit, eine Gewichtung einzubauen, geht über das Ziehen von Stichproben mit Zurücklegen. Jeder der hier 1000 Datensätze hat anfangs die gleiche Wahrscheinlichkeit, gezogen zu werden. Da wir Ziehen mit Zurücklegen betrachten, können in der Stichprobe, die ebenfalls 1000 Datensätze enthält, manche Datensätze mehrfach vorkommen, dafür andere gar nicht. Mit diesen neu erzeugten Daten wird ein Entscheidungsbaum generiert.

Nun folgt die erste Eigenschaft, die als wesentlich für den Erfolg des Boosting-Ansatzes angesehen werden kann: Diejenigen Fälle aus dem Originaldatensatz, die mit einem Baum falsch klassifiziert werden, erhalten im nächsten Iterationsschritt eine leicht erhöhte, die korrekt klassifizierten eine leicht verminderte Ziehungswahrscheinlichkeit. Es wird also automatisch dafür gesorgt, dass sich der Algorithmus mehr um die momentanen Problemfälle kümmert.

Die zweite Zutat zum erfolgreichen Boosting-Ansatz besteht in der abschließenden Gewichtung aller Vorhersagen. Hier wird die Höhe des Gewichtes raffiniert (und theoretisch begründbar) über die Fehlerquote auf dem ursprünglichen Datensatz gesteuert: Durchläufe mit geringer Fehlerquote werden höher, Durchläufe mit hoher Fehlerquote werden niedriger gewichtet.

Es kann passieren, dass bei einem Durchlauf mehr falsch als richtig gemacht wird und die Fehlerquote über 50% liegt. Ein solcher Durchlauf wird ignoriert und die Ziehungswahrscheinlichkeiten werden wieder auf die Ausgangsposition gebracht.

Die folgende Abbildung (bitte klicken Sie auf die Grafik für eine vergrößerte Darstellung!) zeigt den möglichen Ablauf eines Boostingvorgangs:

Alles perfekt dank Boosting

In der ersten Spalte ist die momentan generierte Stichprobe zu den Iterationen 1, 2, 3, 4, dann 20 und schließlich 40 dargestellt. Hier gilt es, eine kleine Hürde bei der Visualisierung zu überwinden: Wie macht man deutlich, dass ein gewählter Datenpunkt mehrfach vorhanden ist? Wird ein Punkt immer auf die gleiche Stelle geplottet, sieht er immer noch unverändert aus. Wir behelfen uns mit einer kleinen addierten Zufallsgröße, um einen mehrfach vorhandenen Punkt “zu verschmieren”.

Die zweite Spalte zeigt das Vorhersageergebnis auf den Originaldaten – und zwar dasjenige des Entscheidungsbaumes, der mit den Daten aus der ersten Spalte gewonnen wurde. Die zusätzliche angegebene Fehlerquote A wird ebenfalls auf dem Originaldatensatz berechnet.

Die dritte Spalte stellt das gewichtete Vorhersageergebnis aller bisherigen Durchläufe dar. B bezeichnet hier den Gesamtfehler auf dem Originaldatensatz und C den Gesamtfehler auf einem unabhängig generierten Testdatensatz.

Betrachten wir einmal die erste Zeile. Das Ergebnis in der mittleren Spalte ist sehr ähnlich zu unserer anfangs dargestellten Entscheidungsbaumprognose. Da nur eine Iteration vorliegt, ist das Gesamtergebnis der dritten Spalte natürlich identisch.

Die Fälle, die falsch klassifiziert wurden, erhalten nun eine höhere Ziehungswahrscheinlichkeit. Die Grafik in der ersten Spalte der zweiten Zeile zeigt einen verstärkten roten Block oben in der Mitte und einen analogen grünen Cluster rechts unten. Wenig überraschend werden Fälle aus diesen Bereichen vom Entscheidungsbaum dieser Runde (Zeile 2, Spalte 2) auch korrekt vorhergesagt.

Wieso sieht das Gesamtergebnis nach der 2. Iteration noch unverändert aus? Dies liegt daran, dass die Prognose des 1. Durchlaufes aufgrund des geringeren Fehlers A=0.164 höher gewichtet wird als die Prognose des 2. Durchlaufes (A=0.205). Wenn der erste Durchlauf “Grün” vorhersagt und der zweite “Rot”, setzt sich somit “Grün” durch.

Verfolgt man nun die Iterationen, sieht man, dass immer dort, wo ein Klassifikator Fehler macht, die Ziehungswahrscheinlichkeit in der folgenden Iteration ansteigt. Der Klassifikator der 2. Iteration sagt bspw. “Grün” für die Gegend bei (0.8, 0.5) vorher, wo eigentlich “Rot” hingehört: Sofort erhält dieser Bereich eine erhöhte Berücksichtigung in der Stichprobe (Zeile 3, Spalte 1).

Hier bei diesem Beispiel ist offensichtlich und auch leicht nachvollziehbar, dass die Fälle nahe der Trennkurve prinzipiell mehr Probleme bereiten. Fälle, die weiter entfernt sind, werden tendenziell eher richtig vorhergesagt und gelangen somit auch seltener in die generierten Stichproben.

Für die abschließende Beurteilung des Boosting-Ansatzes ist natürlich das Gesamtergebnis entscheidend. Bereits nach 40 Iterationen liefert der gewichtete Klassifikator ein überzeugendes Ergebnis ab – nur drei der 1000 Fälle der Originaldaten werden noch falsch klassifiziert. Selbst der Fehler auf der unabhängigen Testmenge beträgt nur 2.1 %.

Obwohl jeder einzelne Entscheidungsbaum nur ein simples Vorhersagemuster erzeugen kann, das mit maximal 4 Rechtecken generiert werden könnte, ist der Gesamtklassifikator in der Lage, die gekrümmte Trennkurve nahezu perfekt nachzubilden – aus den einzelnen schwachen Klassifikatoren wurde in der Tat ein starker, nahezu fehlerloser Klassifikator generiert.