Die Beschreibung von Verteilungen geht oft über die Angabe von Mittelwert und Standardabweichung hinaus. Wir erläutern, was sich bei den hierfür wichtigsten Analysemodulen Boxplot und Verteilungsanalyse im neuen Release getan hat. Zusätzlich wird für das Verständnis nützliches Hintergrundwissen vermittelt.
Boxplot und Verteilungsanalyse
Wenn ein Unternehmen beispielsweise einen bestimmten Gesamtumsatz erzielt, ist dieser sicherlich eine relevante Größe. Genauso – oder noch mehr! – interessiert aber bei der Analyse, ob die einzelnen Kunden zum Umsatz in etwa gleich viel beitragen, oder ob es womöglich nur einen einzigen Großkunden gibt, dessen Ausfall sich auf die Unternehmenssituation spürbar negativ auswirken würde. Mit der Verteilungsanalyse und Boxplots – beide Verfahren habe ich zuletzt im Beitrag Stromerzeugung in Deutschland eingesetzt und in der Anwendung beschrieben – stehen uns in DeltaMaster geeignete Instrumente zur Verfügung.
Mit dem neuen DeltaMaster-Release 6.6.1 lassen sich nun auch für relationale Modelle univariate statistische Analysewerte anlegen. Damit ist es jetzt möglich, auch in relationalen Modellen Quartile – und den Median – berechnen und somit Boxplots verwenden zu können. Die Verteilungsanalyse zeigt mehr Details und liefert weitere Kennzahlen. Auch sie hat ihre Daseinsberechtigung:
Die Details in der Verteilungsanalyse und das Wesentliche im Boxplot
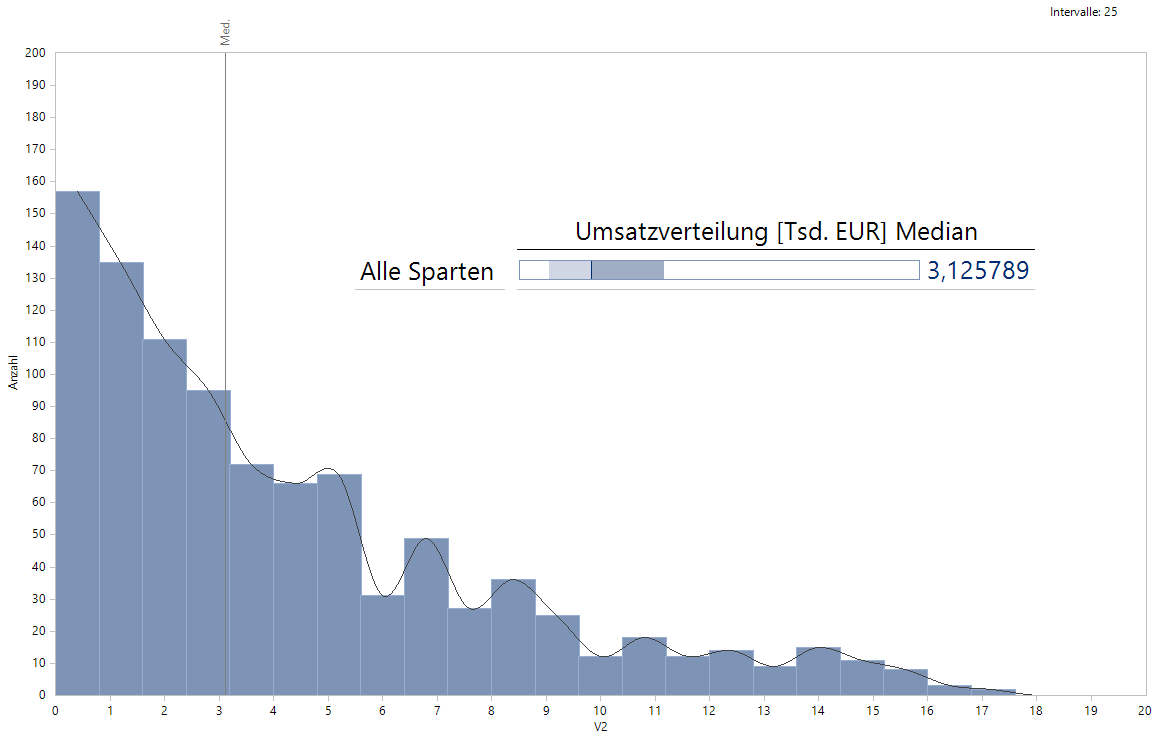
Die Verteilungsanalyse zeigt detailliert die Anzahlen der Kunden mit verschiedenen Umsätzen innerhalb von Umsatzklassen, die durch die Angabe gleichgroßer Intervalle definiert werden. Die Festlegung der Intervalle erfolgt indirekt durch die Angabe der Anzahl der Intervalle.
Der Boxplot zeigt die 5 Größen Minimum, 25%-Quartil, Median, 75%-Quartil und Maximum. Somit entstehen 4 Intervalle, die grob gesprochen jeweils ca. 25 % der Daten enthalten (zu den Details gleich mehr). Auch der Boxplot zeigt, dass die ersten 50 % der Daten links vom Median im Vergleich zu den 50 % der Daten rechts vom Median in einem schmaleren Bereich liegen.
Durch die weitere Unterteilung in 25-Prozent-Segmente sehen wir sogar, dass die Breite der Intervalle ansteigt. Dies ist ein Indiz dafür, dass das Histogramm vermutlich eher eine fallende Tendenz der Säulenhöhen aufweist.
Verteilungen: Exkurs Quantile
Die beobachteten Daten – in diesem Fall Umsätze – werden als unabhängige Realisationen von Zufallsvariablen mit einer festen, aber unbekannten Verteilung interpretiert. Um besser verstehen zu können, was mit den Quartilen und dem Median gemeint ist, betrachten wir zunächst den theoretischen Fall, dass wir die Verteilungsfunktion doch kennen.
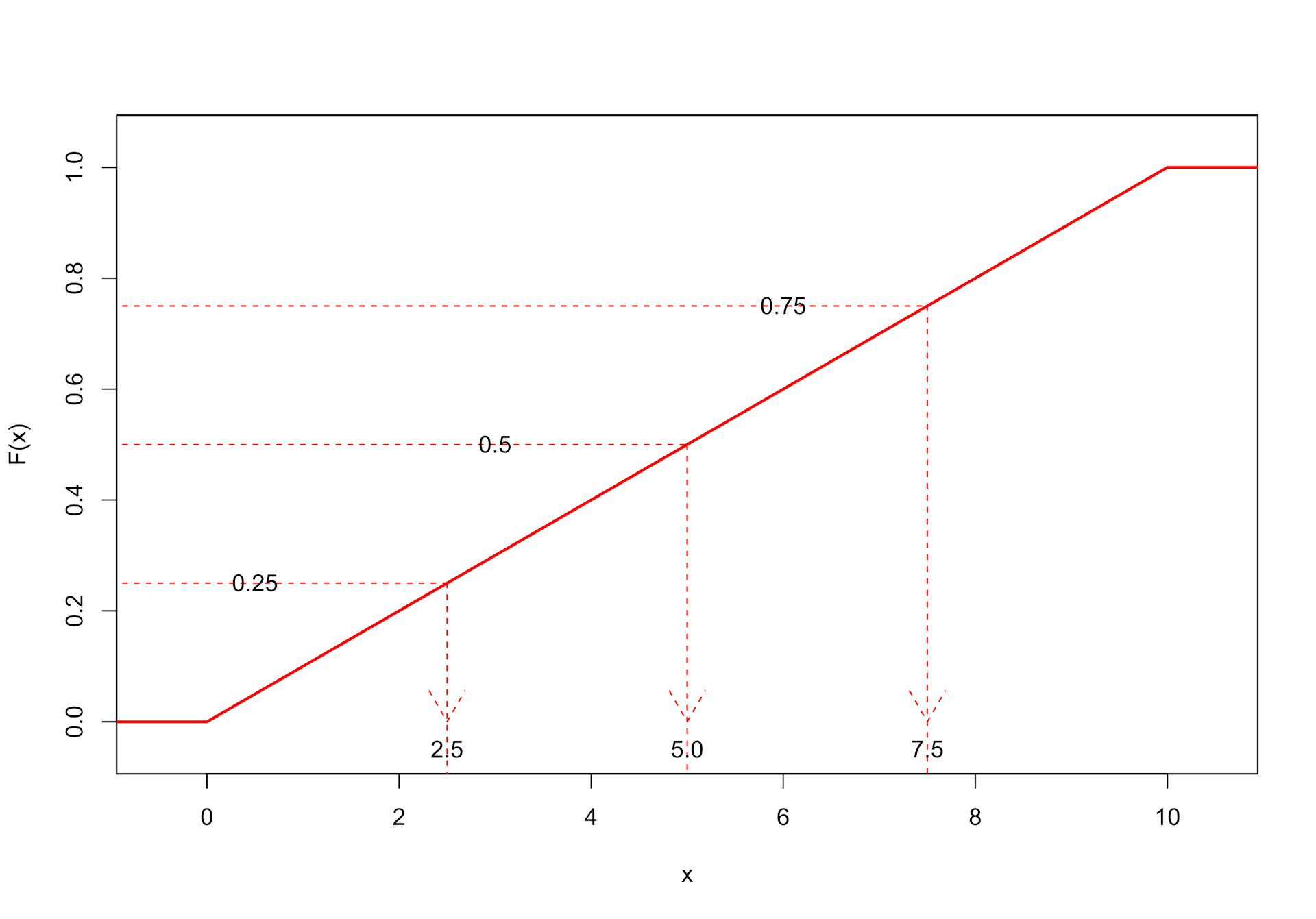
Nehmen wir einmal an, dass die Umsätze auf dem Intervall von 0 bis 10.000 gleichverteilt sind. Die Wahrscheinlichkeit, einen Umsatz zwischen 1.000 und 2.000 Euro zu beobachten, ist dann beispielsweise identisch zu der Wahrscheinlichkeit, dass ein Umsatz zwischen 7.000 und 8.000 Euro liegt, und beträgt p = 0.10. Die unten abgebildete Verteilungsfunktion zeigt nun in Abhängigkeit von einem Umsatzwert x die Wahrscheinlichkeit, dass für einen Kunden ein Umsatz unterhalb dieses Wertes x entsteht. Wenn x von 0 auf 10 [Tsd.] steigt, dann steigt diese Wahrscheinlichkeit linear auf den Wert 1 an. Größere Werte als 10.000 treten nicht auf.
Die Berechnung der Quantile bei einer Gleichverteilung
Möchte man zu einem Wert x die Wahrscheinlichkeit wissen, einen Umsatz unterhalb dieses Wertes x zu erzielen, liest man den zugehörigen Wert einfach aus der Verteilungsfunktion ab. Zu x = 4 [Tsd.] gehört beispielsweise die Wahrscheinlichkeit 0.40.
Bei Quantilen gibt man nun die Wahrscheinlichkeit vor und sucht den passenden x-Wert. Die Quartile Q25 und Q75 und der Median sind Spezialfälle von Quantilen. Die zugehörigen Wahrscheinlichkeiten lauten 0.25, 0.75 und 0.5.
In der Grafik gehen wir bei der Ermittlung von Quantilen nun umgekehrt vor: Wir starten auf der y-Achse mit der gewünschten Wahrscheinlichkeit, gehen nach rechts, bis wir die Verteilungsfunktion treffen, gehen senkrecht nach unten und lesen den Wert auf der x-Achse ab. In unserem Fall ist der x-Wert bei einer Vorgabe y = P(X<=x) mit 0 < y < 1 eindeutig bestimmt, da die Verteilungsfunktion streng monoton wächst.
Wir leiten beispielsweise ab, dass der Median bei 5 [Tsd.] liegt. In der Theorie funktioniert das also problemlos, aber nun kennen wir die „wahre“ Verteilung leider nicht.
Verteilungen: Geschätzte Quantile
Wir haben nun nur eine Stichprobe zur Verfügung. Nehmen wir zunächst an, dass die Stichprobe recht klein ist und wir die folgenden 7 Umsätze [in Tsd. EUR] beobachtet haben, hier sortiert dargestellt:
0.596 1.811 4.505 5.405 6.134 8.636 9.342
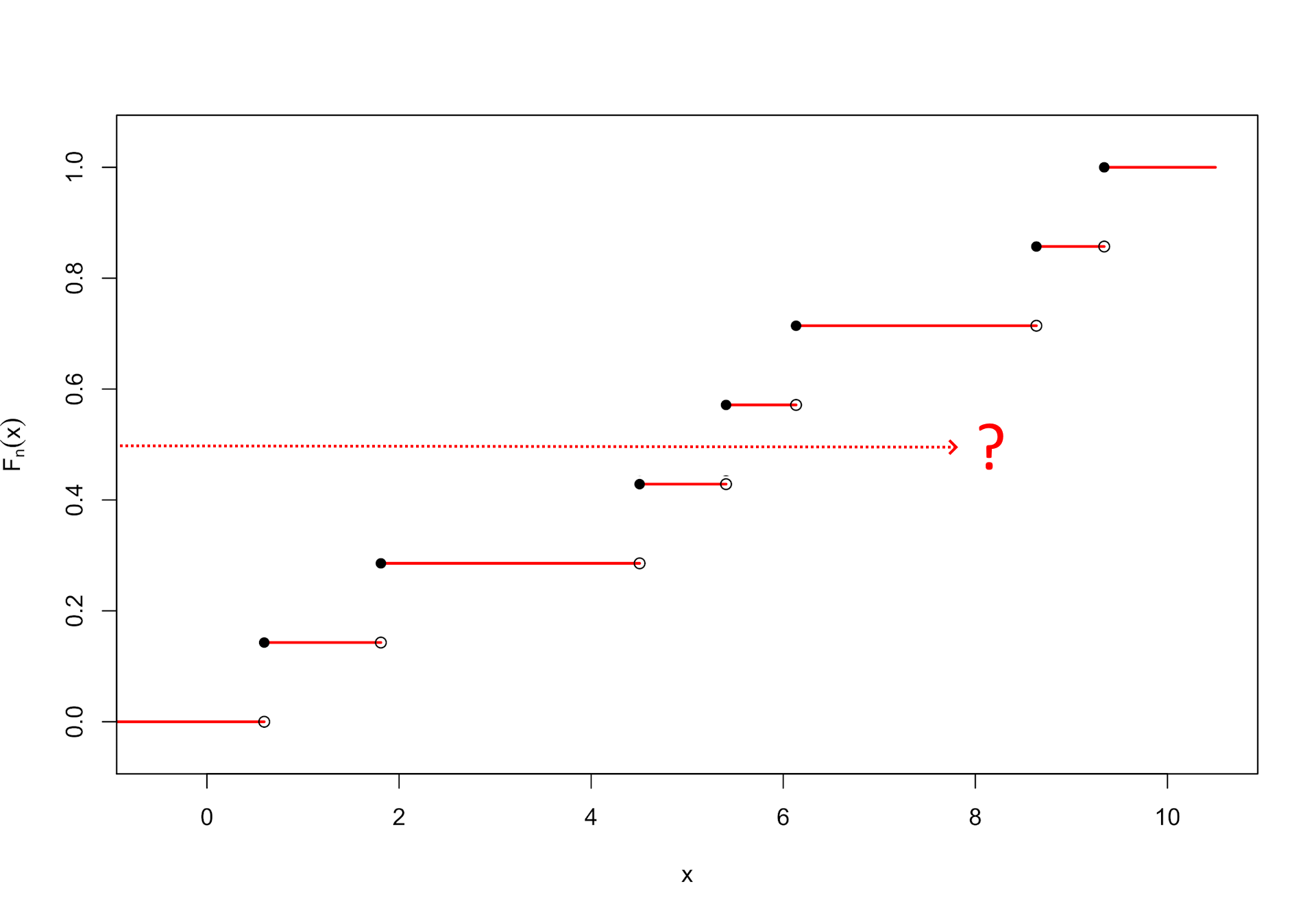
Wir könnten auf die Idee kommen, anstelle der unbekannten wahren Verteilungsfunktion die sogenannte empirische Verteilungsfunktion zu nehmen. Sie zeigt zu einem x den Anteil der Beobachtungen, die kleiner oder gleich diesem Wert x sind. Es entsteht eine Treppenfunktion, die bei jedem neu beobachteten Wert 1 / n (im Beispiel n = 7) nach oben springt:
Problem Schätzung der Quantile
Die im theoretischen Fall geschilderte Vorgehensweise, ein Quantil zu berechnen, ist hier mit Problemen verbunden: Da die empirische Verteilungsfunktion nicht stetig ist, treffen wir die Funktion bei Projektion von links dummerweise gar nicht, wie es die Grafik im Falle des Medians (y = 0.5) vermittelt. Es kann auch sein, dass wir exakt auf der Höhe eines Segmentes liegen und somit gleich ein ganzes Intervall zu diesem Wert y gehört.
Während die theoretischen Quantilswerte (Q25, Median, Q75) eindeutig definiert sind, gibt es bei der Schätzung aufgrund einer Stichprobe eine Reihe von Verfahren, die auch zu unterschiedlichen Quantilsschätzern für die gleiche Größe kommen können.
Schätzung der Quantile
Rob J. Hyndman hatte bereits 1996 gängige Statistikpakete auf verwendete Verfahren untersucht (Rob J. Hyndman; Yanan Fan, The American Statistician, Vol. 50, No. 4. (Nov., 1996), pp. 361-365. Sample Quantiles in Statistical Packages) und bereits damals 9 verschiedene Varianten ermittelt, um Quantilsschätzer zu berechnen. Das Statistik-Software-Paket R stellt im Befehl quantile(data,p,type=k) diese 9 Varianten in Form des Wertes k (k=1, …, 9) zur Verfügung. Auch in DeltaMaster werden je nach Modellierungsumgebung unterschiedliche Varianten eingesetzt.
Diese Konstellation ist historisch gewachsen, da manche Datenbank-Umgebung erst mit späteren Versionen spezialisierte Funktionen zur Verfügung stellte. Wundern Sie sich also nicht, wenn Sie bei denselben Daten je nach Modellierung möglicherweise unterschiedliche Quartilsschätzer sehen. Der Median ist hiervon bei den von uns eingesetzten Verfahren nicht betroffen – er ist bei allen eingesetzten Typen identisch.
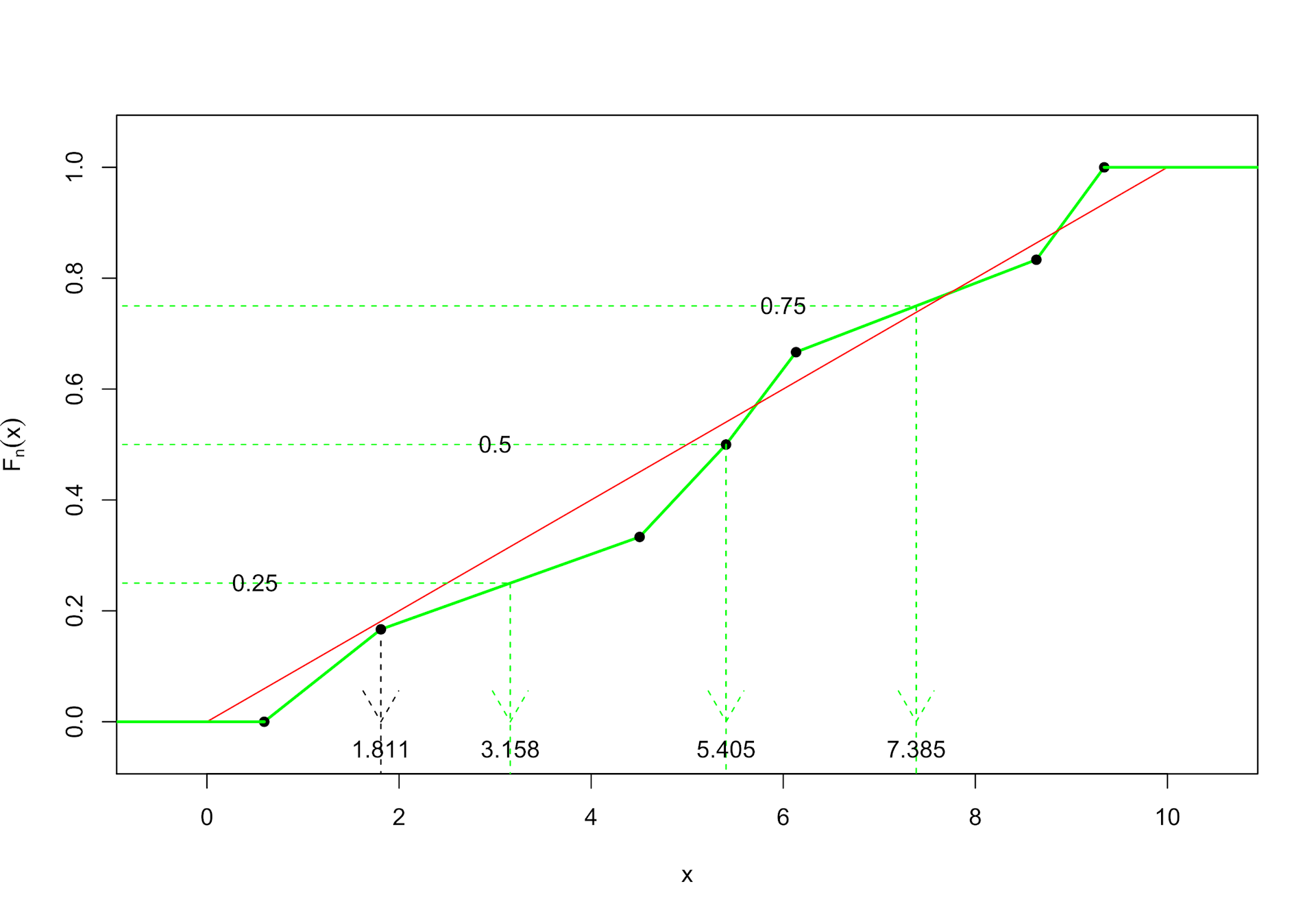
Die Variante 2, die in DeltaMaster zum Beispiel im Selfservice Microsoft Excel MDX Analytics eingesetzt wird, nimmt im obigen Bild der empirischen Verteilungsfunktion denjenigen x-Wert, bei dem die empirische Verteilungsfunktion zum ersten Mal über dem gewünschten y-Wert liegt. Bei y = 0.5 ist dies beim 4. Wert 5.405 der Fall. Ebenso entspricht der Q25-Schätzer dem 2. Wert 1.811 und der Q75-Schätzer dem 6. Wert 8.636.
Sollte ein ganzes Intervall auf der gewünschten Höhe liegen, wird der Mittelwert der beiden Enden genommen. Bei einer Stichprobengröße von 8 liegt dieser Fall beim Median vor und der Stichproben-Median ergibt sich als Mittelwert der 4. und der 5. Beobachtung in der sortierten Liste.
Quantile auf dem SQL Server
Im neuen Release können Sie nun auch bei relationalen Anwendungen univariate statistische Analysewerte wie Q25 und Q75 anlegen. Sollten Sie auf einem hinreichend aktuellen neuen SQL-Server (laut ChatGPT ab SQL Server 2012) unterwegs sein, wird dann bereits von Haus aus eine Funktion PERCENTILE_CONT (CONT für continuous) zur Verfügung gestellt, die wohl dem Typ 7 bei Hyndman entspricht und von DeltaMaster verwendet wird. Solche bereits implementierten Funktionen schlagen üblicherweise die Performanz von nachgebauten Lösungen. Die Funktionsweise dieses Verfahrens wird in der folgenden Grafik erläutert:
Ansatz mit Typ 7
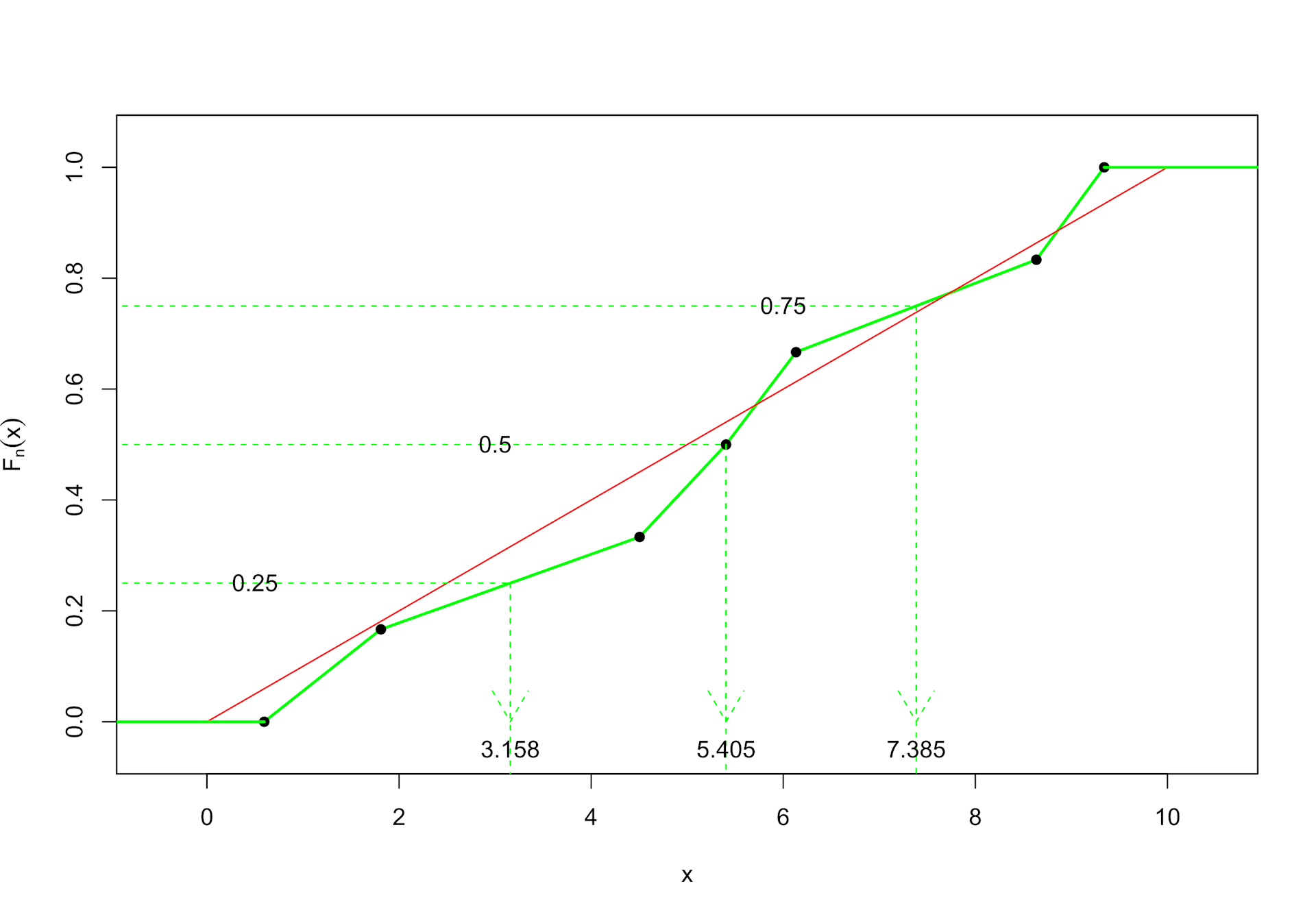
Es wird ein stückweise linearer Linienzug gebildet. Er beginnt bei der ersten Beobachtung mit der Höhe 0 und endet mit der letzten Beobachtung auf der Höhe 1. Dazwischen wird jeder beobachtete Wert um 1 / (n-1), also im Beispiel um 1 / 6 höher eingezeichnet. Sollten Doubletten vorhanden sein, können auch senkrechte Segmente auftauchen.
Mit dieser Konstruktion erhalten wir eine Annäherung der unbekannten Verteilungsfunktion (bzw. genauer genommen der Umkehrfunktion auf dem offenen Intervall (0;1) ) und können wieder das bei der wahren Verteilungsfunktion eingesetzte Prinzip benutzen. Im Bild sehen wir, wie die Quartilsschätzer und der Median für die Stichprobe ermittelt werden. Bei 7 Beobachtungen liegt der 4. Wert 5.405 genau auf Höhe 3 / 6 = 0.5 und wir erhalten somit diesen konkreten Wert als Median. Bei den Quartilen wird bei n = 7 zwischen jeweils zwei Werten interpoliert.
Einfluss der Stichprobengröße
Zeichnen wir einmal das Quartil Q25, wie es mit Typ 2 berechnet wird, mit in die Grafik ein:
Q25, mit Typ 2 berechnet
Bei einer kleinen Stichprobengröße können sich die Unterschiede im berechneten Wert des Quartils je nach Typ schon einmal bemerkbar machen. Erhöhen wir nun die Stichprobengröße auf 100:
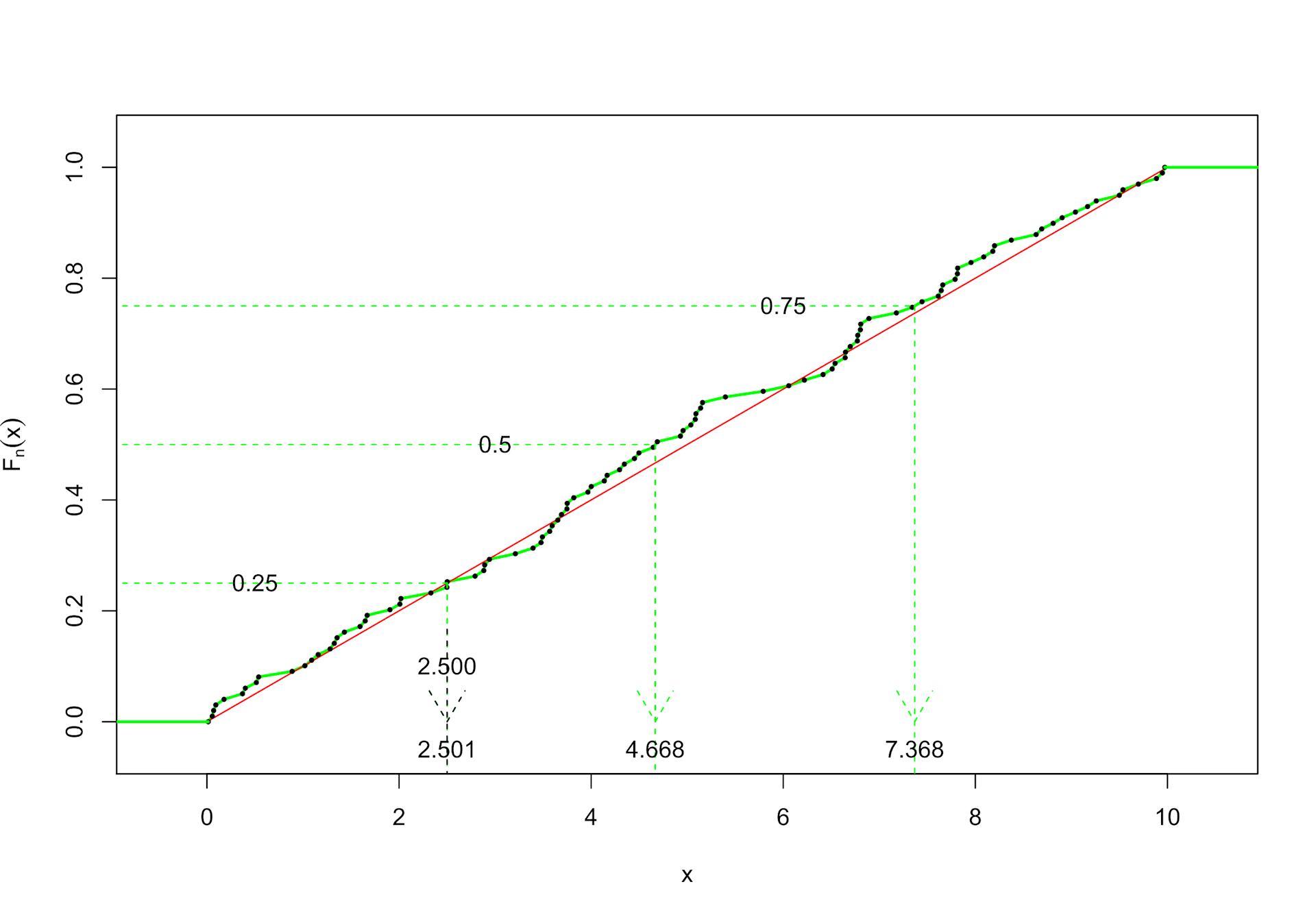
Q25 für Typ 2 und Typ 7 bei n = 100
Wie man sehen kann, verschwinden die Unterschiede der Verfahren bei größeren Stichproben. Typ 2 liefert den Q25-Schätzer 2.500 und Typ 7 den Schätzer 2.501.
Bei der stetigen wahren Verteilungsfunktion gilt, dass die Wahrscheinlichkeit exakt 0.25 beträgt, einen Umsatz zu beobachten, der kleiner oder gleich dem Quartil Q25 ist. Ebenso beträgt die Wahrscheinlichkeit genau 0.25, zwischen Q25 und Median zu landen.
Für die Schätzer einer Stichprobe gilt das nur näherungsweise. Im Beispiel mit 7 Beobachtungen betragen die wahren Verteilungsfunktionswerte 18.11 % beim Q25-Schätzer vom Typ 2 bzw. 31.58 % bei Typ 7; diese Werte liegen noch ein Stück vom gewünschten Wert 25 % entfernt. Für die Stichprobe selbst liegen bei beiden Typen jeweils 2 von 7 Beobachtungen unterhalb des Q25-Schätzers. Dies entspricht etwa 28,6 %.
Für wachsende Stichproben gilt aber, dass sich die Stichprobenanteile unterhalb und inklusive des Quartilsschätzers allmählich den 25 % annähern. Analoges gilt für die Schätzer von Median und Q75 mit 50 bzw. 75 anstelle der 25 Prozent. Bei höheren Stichprobengrößen ist es also nicht verkehrt zu behaupten, dass jedes Intervall des Boxplots ca. 25 Prozent der Daten enthält.
Verteilungen: Der Boxplot im Einsatz
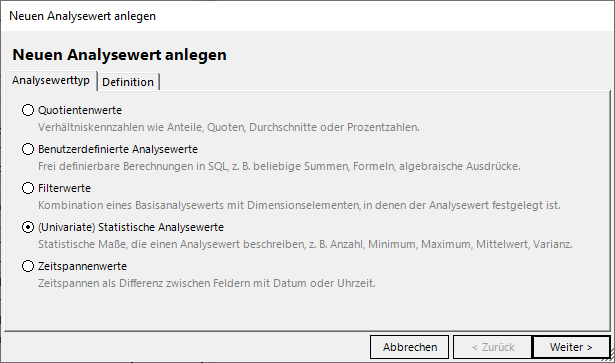
Um einen Boxplot auch in relationalen Modellen zeichnen zu können, müssen 6 univariate statistische Analysewerte angelegt werden. Mit dem aktuellen Release 6.6.1 gibt es nun nicht nur bei OLAP-, sondern auch bei relationalen Modellen die Möglichkeit, den passenden Punkt auszuwählen:
Neue statistische Analysewerte anlegen
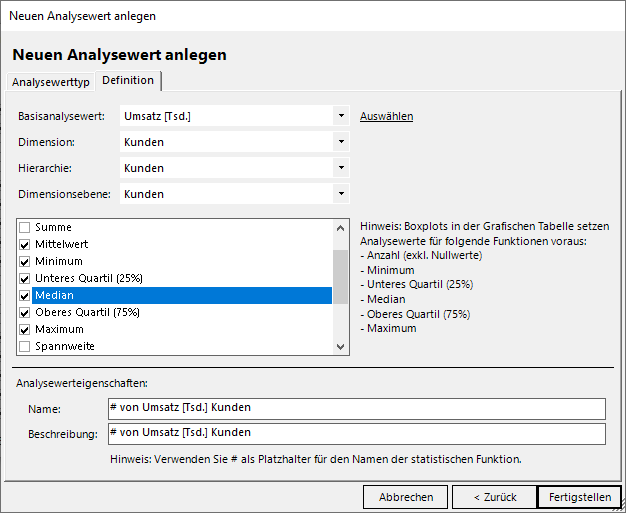
Für einen Boxplot legen wir im folgenden Menü zwingend die auch im sichtbaren Hinweis genannten 6 Analysewerte an. Darüber hinaus gäbe es weitere, für den Boxplot nicht relevante Kennzahlen wie Varianz oder Spannweite, die wir hier auswählen könnten. Zur Definition benötigen wir neben dem Basisanalysewert noch die Ebene der Dimensionselemente:
Benötigte Kennzahlen für Boxplot
Mehrere Boxplots
In einer Grafischen Tabelle kann man einen Boxplot über Editieren/Grafik aktivieren, wenn sich entweder der Median oder der Mittelwert auf der Spaltenachse befindet. Wir sehen im Balken aber immer die 5 Werte Minimum, Q25, Median, Q75 und Maximum. Dies gilt auch, wenn der Boxplot zur Kennzahl des Mittelwerts aktiviert wird.
Auf einer Spaltenachse können wir nur ein Boxplot-Diagramm aktivieren. Bei mehrere Median-Kennzahlen erhält nur die erste den Boxplot-Kasten. Iterieren wir aber über die Elemente einer weiteren Dimension, vorzugsweise auf der Zeilenachse, können wir mehrere Boxplots gut vergleichen, da sie dann übereinanderstehen.
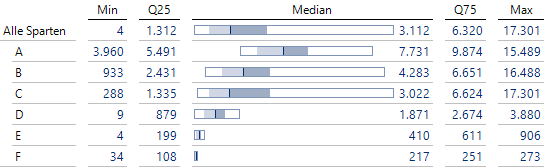
Liegen etwa verschiedene Produktsparten vor, könnte das beim Beispiel aus der ersten Grafik so aussehen:
Verteilungen in den Sparten vergleichen
Hier zeigt sich der Vorteil des Boxplots: Auf kleiner Fläche können Verteilungen getrennt nach Elementen einer weiteren Dimensionsebene leicht verglichen werden. Die Angabe der Größen außer dem Median ist optional: Sie müssen nur zwingend definiert, aber nicht unbedingt auf der Achse sichtbar sein!
Auch eine höhere Ebene in der Kundenhierarchie, z. B. Regionen, kann auf der Zeilenachse eingesetzt werden.
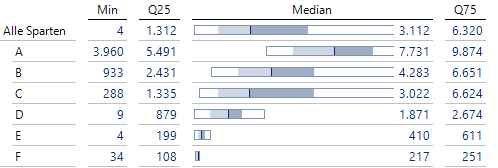
Im konkreten Fall kann man auch das Anzeigeintervall manuell überschreiben. Haben wir bereits die Maxima begutachtet und interessieren uns eher für die Lagen der linken 75 %, schränken wir über Eigenschaften (bzw. F4)/Grafik(2) das Intervall beispielsweise auf 0 bis 11 [Tsd.] ein:
Verteilungen in den Sparten vergleichen, Intervall eingeschränkt
Es existiert auch eine Option einer automatischen Einschränkung, die dann greift, wenn beispielsweise ein Boxplot von vielen gänzlich woanders positioniert ist. Dann wird das Intervall so eingestellt, dass die Boxplots in der Überzahl angemessen dargestellt werden.
Neues Detail in der Verteilungsanalyse
Um die Sparten mittels der Verteilungsanalyse zu vergleichen, wären mehrere Berichte nötig: für jede Sparte ein eigener Bericht. Für einen schnellen Vergleich ist die Grafische Tabelle mit Boxplots besser geeignet.
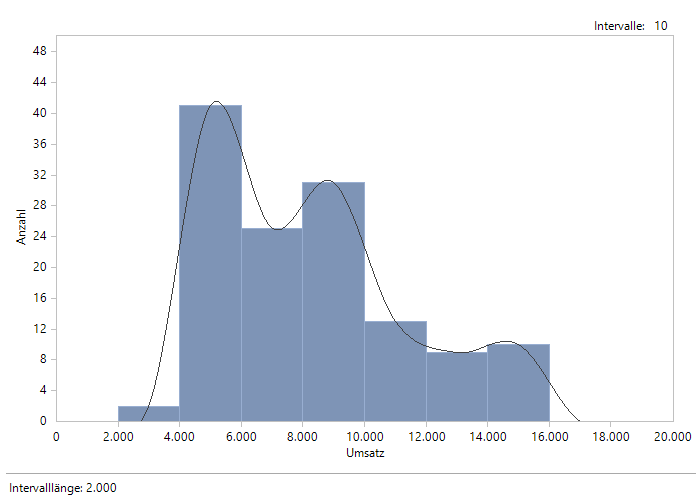
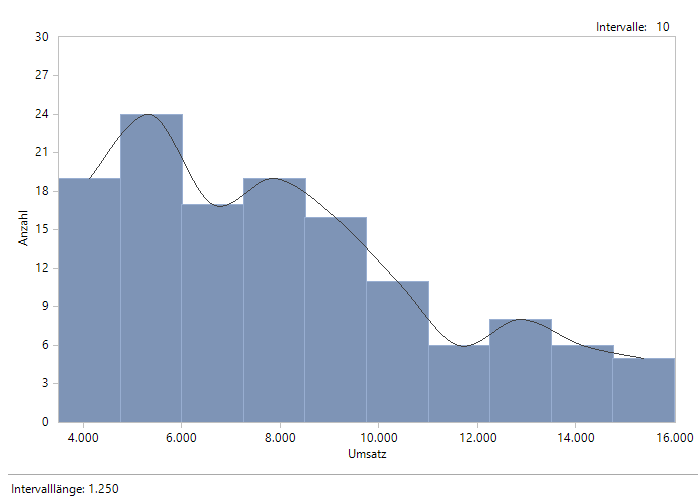
Die Daten zur Sparte A passen aber, um die im Release 6.6.1 eingeführte Neuerung in der Verteilungsanalyse zu erläutern. Schauen wir zunächst auf das Histogramm, das für Sparte A entsteht:
Histogramm mit Luft an den Seiten
Einige Kunden wünschten, dass DeltaMaster den verfügbaren Platz für das Histogramm komplett ausschöpft. Bisher war das schon möglich, indem der Wertebereich für Grafikachsen direkt in den Eigenschaften des Analysewerts knapper bemessen wurde. Nun gibt es zusätzlich unter den Einstellungen der Verteilungsanalyse die Möglichkeit, das Anzeigeintervall der Achse zu verkleinern. In der Statistik der Verteilungsanalyse – oder in der Grafischen Tabelle von oben – lesen wir ab, dass das Minimum in Sparte A bei 3.960 und das Maximum bei 15.489 liegt.
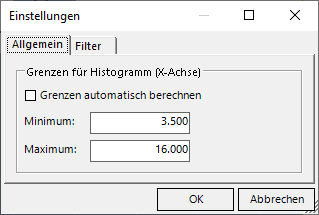
Stellen wir somit einmal Grenzen von 3.500 und 16.000 ein:
Einstellung für Histogramm ohne Luft an den Seiten
Nun nutzt DeltaMaster den verfügbaren Raum für das Histogramm:
Histogramm ohne Luft an den Seiten
Natürlich sind nun die Intervallgrenzen krummer als vorher. Man beachte, dass die eingestellten Grenzen keine Daten abschneiden dürfen:
Unerlaubte Einstellung für Histogramm
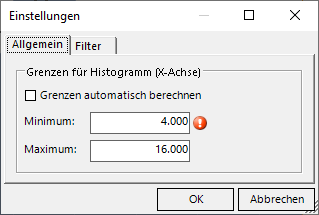
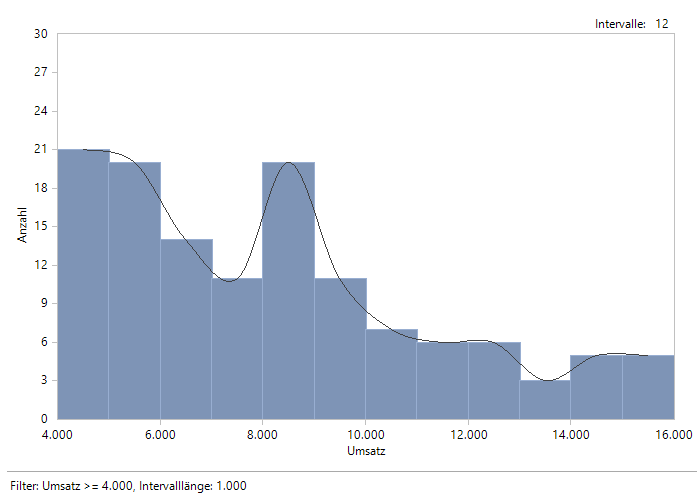
Möchten wir ein Histogramm für diesen Ausschnitt erstellen, müssen wir begleitend auf dem anderen Reiter einen Filter Umsatz >= 4000 setzen, dann ist diese Einstellung erlaubt und wir sehen ein Histogramm für die beschnittenen Daten:
Histogramm für eingeschränkte Daten
Hier haben wir auch wieder schönere Intervallgrenzen. Die Statuszeile erinnert uns an den aktiven Filter.